基于相关峭度共振解调的滚动轴承复合故障特征分离方法
胡爱军,赵 军,孙尚飞,黄申申
(华北电力大学 机械工程系,河北 保定 071003)
当轴承的内圈、外圈、滚动体或保持架中发生局部故障时,产生的周期性冲击会激起轴承及相邻各部件的共振响应。共振解调是轴承故障特征提取和分离的有效方法[2],传统的共振解调技术在确定高频共振频带时,共振频带的中心频率和带宽需要人工选择,无法满足工程的广泛应用[3-4]。针对此问题,Antoni[5-6]提出了基于带通滤波器组的快速谱峭度算法,通过计算和比较各子频带的谱峭度自适应地定位共振频带,在轴承故障特征提取中取得了良好效果。文献[7]将谱峭度应用到轴承复合故障分析中,分别解调外圈及内圈故障激起的共振频带,实现了轴承复合故障特征的分离。但是,文献[8-9]指出,快速谱峭度算法容易受较高峰值脉冲的干扰,可能无法正确定位共振频带。同时,在轴承复合故障信号中,每一个轴承故障都可能会激起多个共振频带,当不同共振频带之间的峭度相差较大时,相对较小峭度的共振频带容易被掩盖,对复合故障特征的分离产生不利的影响。考虑到轴承故障冲击的周期特性,文献[10]提出了相关峭度的概念,并以其为目标函数解卷积出被噪声掩盖的连续性冲击信号。
综上所述,本文以相关峭度为评价指标,提出了基于相关峭度的共振解调方法。该方法沿频率轴平移滤波窗,通过设定不同故障的解卷积周期,计算每个带通滤波信号的相关峭度,形成不同故障解卷积周期的相关峭度曲线,根据筛选出的目标相关峭度曲线的最大值选择多个共振频带,进行共振解调处理。对不同能量多共振频带的内、外圈复合故障仿真及实验分析,表明该方法能够有效分离出不同部件故障频率占优的共振频带,实现了复合故障的准确分离。
1 基于相关峭度的共振解调方法
1.1 相关峭度
峭度是信号尖峰的量度,是检测旋转部件故障冲击性的重要指标。对于零均值信号yn的峭度(Kurtosis)表达式为
(1)
峭度只能表征瞬态脉冲的强度,但它不能区分在滚动轴承振动信号中循环产生的脉冲,无法衡量周期性脉冲故障所占的比重。因此,可能导致错误的共振频带识别结果,进而误导滚动轴承故障诊断结果。相关峭度(Correlated Kurtosis,CK)是近年在峭度基础上提出的,对于零均值信号yn的相关峭度表达式为
(2)
式中:T为冲击信号感兴趣的周期;N为信号的采样点数;M为移位的周期个数。
值得注意的是当T=0,M=1时,相关峭度将退化为峭度定义。与峭度相比,相关峭度具有了周期相关函数的特性,能充分考虑故障信号中所含设定周期T的冲击成分的连续性。可以根据不同相关峭度值的大小判断不同信号中含有的感兴趣故障脉冲所占的比重。
中国石油石化:中国环保风暴不断升级,给石化行业产生了巨大的压力。各位认为中国石化企业应当如何看待这种压力?
1.2 频带平移的共振带搜索算法
本文采用的频带平移方法是沿频率轴平移一个给定滤波窗来完成。首先对时间信号x(k)进行傅里叶变换,转换为频域信号X(n)。
于是基于当前平移窗的频域信号可表示为
Xw(P)=X(n)w(n-a)
(3)
式中:w(n-a)为在频率轴的右移窗口;P为给定窗口长度;a为每次窗口移动距离。
对当前频带信号做傅里叶逆变换,得的滤波信号为xw(k),滤波信号的相关峭度计算表达式为
(4)
根据式(4),在全频范围内计算每个子频带滤波信号的相关峭度,得到不同故障解卷积周期下的相关峭度曲线。
为了有效筛选出目标相关峭度曲线,首先对信噪比不同、周期为T的冲击信号做定量分析。当分析点数为32 768点时,相关峭度值的数量级为10-5。设定解卷积周期=T和周期≠T时对应的相关峭度值如表1、表2所示。由表分析可得,当相关峭度值大于3.2时,可以说明信号中含有周期为T的故障脉冲,并且信噪比越高的信号(相当于本文方法的当前滤波窗滤波效果较好)所对应设定解卷积周期=T时的相关峭度值越大,而对应设定解卷积周期≠T时的相关峭度值越小。所以,从多条相关峭度曲线中筛选目标曲线的准则可总结为:
(1)相关峭度曲线中具有明显的最大值。
(2)相关峭度曲线中最大值应>3.2。

表1 解卷积周期=T时的相关峭度值Tab.1 Correlation kurtosis value at shift period =T

表2 解卷积周期≠T时的相关峭度值Tab.2 Correlation kurtosis value at shift period ≠T
考虑到初始窗口宽度和窗口重叠率等参数对共振带选择的影响,据文献[11]指出的频谱中存在3次谐波时所对应的峭度值最大原则,本文选定初始窗及滤波带宽为3倍故障特征频率、窗口重叠率为0.5,完成窗口的平移。
1.3 共振解调方法流程
本文以相关峭度值为依据,在全频范围内搜寻多个共振频带。提出了基于相关峭度共振解调的滚动轴承复合故障分离方法,首先根据不同的轴承故障特征频率,设定不同故障的解卷积周期及沿频率轴平移滤波窗宽;然后计算每个平移窗滤波信号的相关峭度,形成的不同故障解卷积周期的相关峭度曲线;最后根据目标相关峭度曲线的最大值选择多个共振频带,并进行共振解调处理。整体算法流程如图1所示。

图1 本文算法流程图Fig.1 Flowchart of proposed algorithm
2 仿真信号分析
滚动轴承故障中,轴承单点故障可能会激起多个共振频带[12],同时,多故障条件下,不同故障分别会激起不同共振频带[13-14]。并考虑到在实际故障中,不同轴承故障激起的共振频带,可能会具有不同的能量。为了使仿真分析更具有普适性,本文采用不同能量的多共振频带滚动轴承内、外圈复合故障仿真模型,即,fn1主要由外圈故障激起(具有微弱的内圈故障),fn2主要由内圈故障激起(具有微弱的外圈故障),但两个共振频带具有不同能量。具体仿真信号为
(5)
式中:S1,S2为内圈故障分别在fn1,fn2处激起的幅值,取0.2和0.8;S3,S4为外圈故障分别在fn1,fn2处激起的幅值,取0.5和0.2;转频fr为25 Hz;共振频率fn1为1 500 Hz,fn2为3 800 Hz;衰减系数C为600;内圈故障特征频率fi=1/T1=128 Hz,外圈故障特征频率fo=1/T2=100 Hz;n(t)为加入的的高斯白噪声,信噪比为-8 dB;仿真采样频率为12 800 Hz,分析点数为32 768点。
仿真信号的波形、频谱及包络谱如图2所示。从图2(a)的时域信号中看不出明显的周期性冲击成分;在图2(b)频谱图的低频成分中并未找到相应的故障特征频率,谱线幅值较大的集中分布于2个频率带内;从图2(c)可知,两个故障的特征频率及多阶倍频彼此交错在一起,谱线比较杂乱,若能将信号分离成两个具有不同故障特征的信号,将有利于故障的准确诊断。

图2 仿真信号的波形、频谱和包络谱Fig.2 Waveform,spectrum and envelope spectrum of simulation signal
利用本文所提方法对复合故障仿真信号进行分析,结果如图3所示。图3(a)为设定解卷积周期T分别为内、外圈故障周期时所对应的相关峭度曲线。设定外圈故障相关峭度曲线的最大值为中心频率(1 512)(与固有频率fn1相吻合),取故障特征频率的3倍(300 Hz)为带宽对仿真信号进行共振解调处理,图3(b)为滤波信号的包络谱,谱线清晰且仅存在外圈故障特征频率及其倍频成分,外圈故障信号被成功分离出来。同样,依据内圈故障相关峭度曲线,滤波信号的包络谱分析结果如图3(c),内圈故障特征频率及其多阶倍频,转频及转频调制边带等成分谱线幅值明显,内圈故障信号被成功分离出来。通过不同能量的多共振频带轴承复合故障仿真分析验证了本文能够准确识别出由内、外圈个自激起的共振频带,解调出两个不同频率占优的故障信号,比较理想地实现了内、外复合故障特征的分离。
采用快速谱峭度方法与本文所提方法进行对比,图4为快速谱峭度图的处理结果。图中明显呈现出由内圈激起的共振频带,由外圈激起的共振频带显示比较微弱(虚线)。一般情况下,仅选择最强的共振带进行共振解调处理,只会分离出轴承内圈故障,而外圈故障容易被忽略。

图3 本文所提方法的复合故障仿真信号分析结果Fig.3 Analysis results of compound fault simulated signal by proposed method
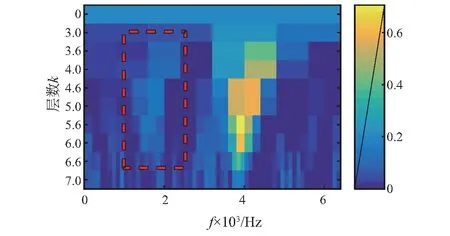
图4 复合故障仿真信号的快速峭度图Fig.4 Fast kurtogram of compound fault simulated signal
3 实测信号分析
使用QPZZ-Ⅱ型旋转机械故障实验台进行复合故障实验,实验台结构如图5(a)所示。采用LYC6205E型深沟球轴承,利用线切割在滚动轴承内、外圈滚道上加工出深度为1.5 mm,宽度为0.2 mm的凹槽。利用PCB压电加速度传感器来拾取故障轴承运行过程中产生的振动信号,复合故障轴承和传感器的安装如图5(b)、图5(c)所示。实验中,电
机转速为1 466 r/min,采样频率为12 800 Hz。表3为实验轴承的结构参数,根据结构参数计算得到的外圈故障特征频率fo=87.59 Hz,内圈故障特征频率fi=132.3 Hz,保持架故障特征频率fc=9.73 Hz,滚动体故障特征频率fb=57.57 Hz。
实验中采用相同的内、外圈复合故障轴承,分别将外圈故障置于6点钟位置和12点钟位置,进行2次实验,用以模拟外圈处于不同载荷下与内圈的复合故障。当外圈故障位于处于6点钟方向时,外圈故障点承载最大,由外圈故障激起的共振频带的能量也就相对较大,当轴承故障位于处于12点钟方向时情况相反。
3.1 外圈故障位于6点钟位置的复合故障分析
实测复合故障信号1的波形、频谱及包络谱如图6所示。从图6(a)故障信号的时域波形中可以看到明显的冲击成分;图6(b)频谱中,幅值较大的谱线集中分布于3 000 Hz以下,在低频段内未发现故障特征频率;信号的包络谱如图6(c)所示,从图6(c)可知,幅值较高的外圈故障特征频率和幅值相对较低内圈故障特征频率相互交叉在一起。

图5 故障实验测试平台、复合故障轴承、传感器安装位置Fig.5 Fault experiment test platform,compound fault bearing and sensor installation position

表3 滚动轴承结构参数Tab.3 Structural parameters of rolling bearing
同时利用基于相关峭度的共振解调方法和基于快速谱峭度解调方法对复合故障信号进行分析,结果分别如图7和图8所示。图7(a)为设定解卷积周期T分别为内圈、外圈、保持架和滚动体故障周期时所对应的相关峭度曲线。根据筛选目标曲线的准则,内圈与外圈相关峭度曲线中具有明显最大值,并且最大值明显大于3.2。分别取这两条相关峭度曲线的最大值作为带通滤波的中心频率(1 411 Hz,4 846 Hz)进行共振解调得到的包络谱如图7(b)和图7(c)所示。图8(a)为快速谱峭度图结果,图中呈现出两个明显的共振频带,频带1的中心频率取2 400 Hz,带宽为800 Hz;频带2的中心频率取6 000 Hz,带宽为800 Hz。利用这两个频带参数对信号进行带通滤波信号的包络谱如图8(b)和图8(c)所示。

图6 实测信号1的波形、频谱和包络谱Fig.6 Waveform,spectrum and envelope spectrum of measured signal 1
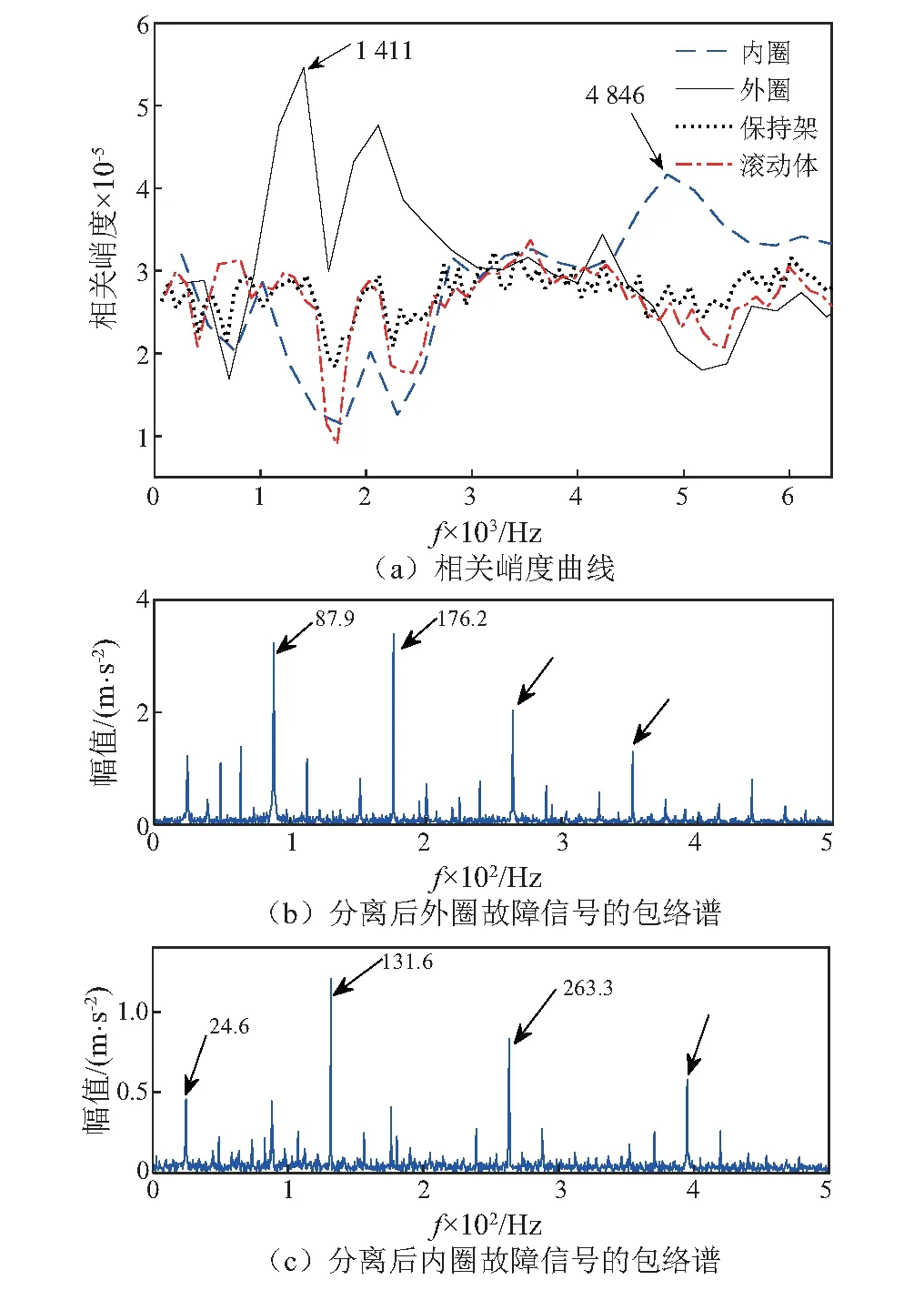
图7 本文所提方法对实测信号1的分析结果Fig.7 Analysis results of measured signal 1 by proposed method
对比两种方法的处理结果,虽然两者定位的共振频带有所不同,但从解调包络谱来看,都找到了内、外圈各自占优的共振频带,将单通道复合故障信号分解成两个不同频率占优的通道中。表明,当轴承故障处于此状态下两种方法都能够实现轴承复合故障的准确分离。

图8 快速谱峭度方法对实测信号1的分析结果Fig.8 Analysis results of measured signal 1 by fast kurtogram
3.2 外圈故障位于12点钟位置的复合故障分析
实测复合故障信号2的波形、频谱及包络谱如图9所示。从图9(a)故障信号的时域波形中看出周期性特征不明显的冲击成分;从图9(b)可知,滚动轴承故障激起的能量比较分散,遍布于整个频带范围,看不出所激起系统的固有频带,并且在低频段内未发现故障的特征频率;从图9(c)可知,两种故障频率相互交叉在一起,需要对信号做进一步的分离工作。
首先利用本文所提方法对复合故障信号进行分析,结果如图10所示。图10(a)为滚动轴承典型的4种故障对应的相关峭度曲线,根据筛选目标曲线的准则,分别取内、外圈相关峭度曲线的最大值作为带通滤波的中心频率进行共振解调;从包络谱图10(b)可知,轴承外圈故障的特征频率及其多阶倍频;从图10(c)可知,轴承内圈故障的特征频率及多阶倍频。本文方法能够成功找到内、外圈故障激起的各自占优共振频带,解调出两个不同频率占优的故障信号,比较理想地实现了内、外复合故障特征的分离。

图9 实测信号2的波形、频谱和包络谱Fig.9 Waveform,spectrum and envelope spectrum of measured signal 2
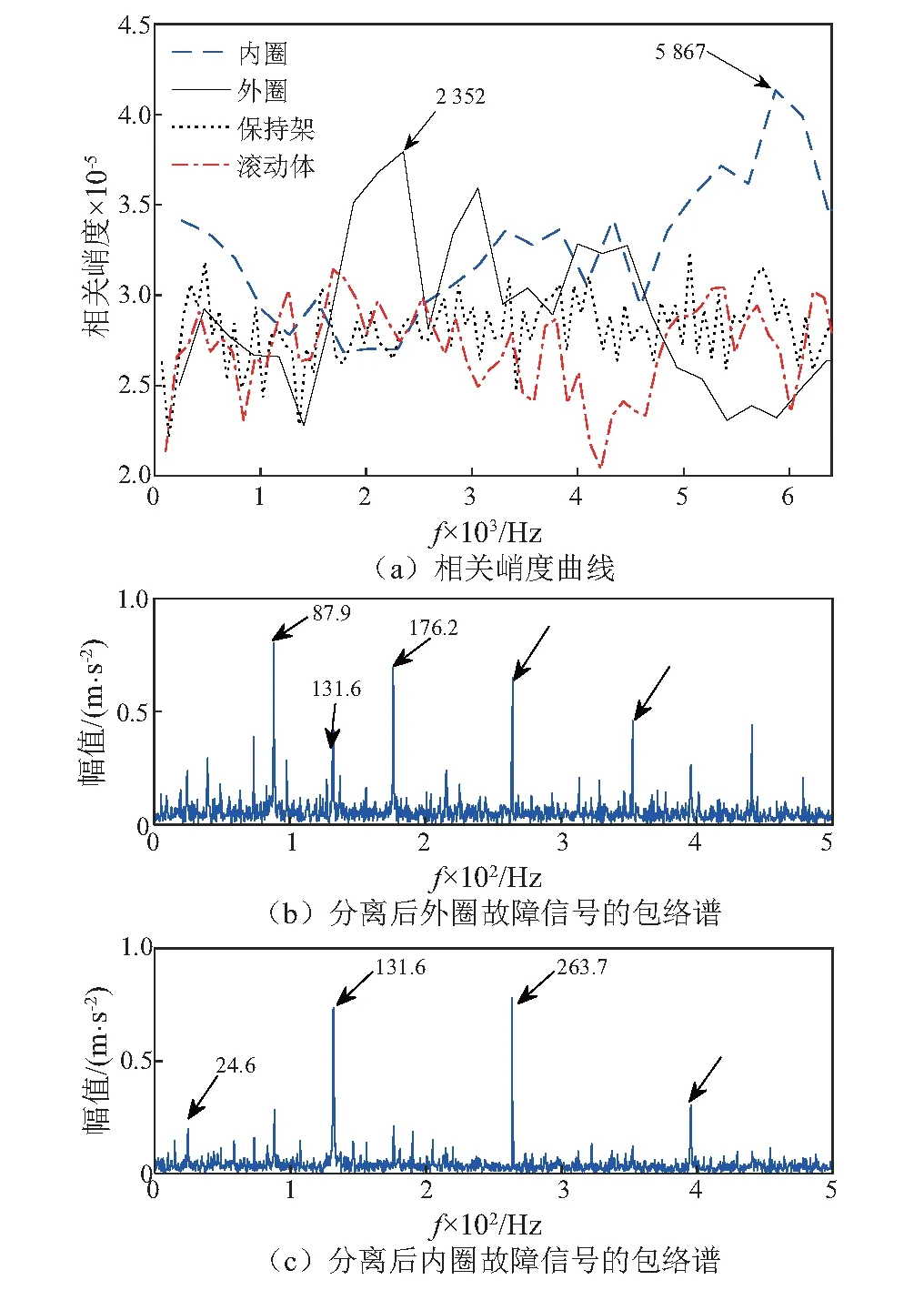
图10 本文所提方法对实测信号1的分析结果Fig.10 Analysis results of measured signal 1 by proposed method
与本文所提方法进行对比,采用快速谱峭度方法分解实测复合故障信号2。图11(a)为快速谱峭度图的结果,图中只呈现出1个明显的共振频带。频带的中心频率取4 400 Hz,带宽为800 Hz,利用这个频带对信号进行带通滤波。滤波信号的包络谱如图11(b)所示,与图9(c)比较可知,仅仅增强了内、外圈故障特征频率,但并未成功的找到两个故障所激起的各自占优的共振频带,不能有效的将复合故障信号分离到两个单独频率占优的通道中。经过对比可知,本文方法在处理复合故障特征分离问题上要比快速谱峭度方法具有优越性。
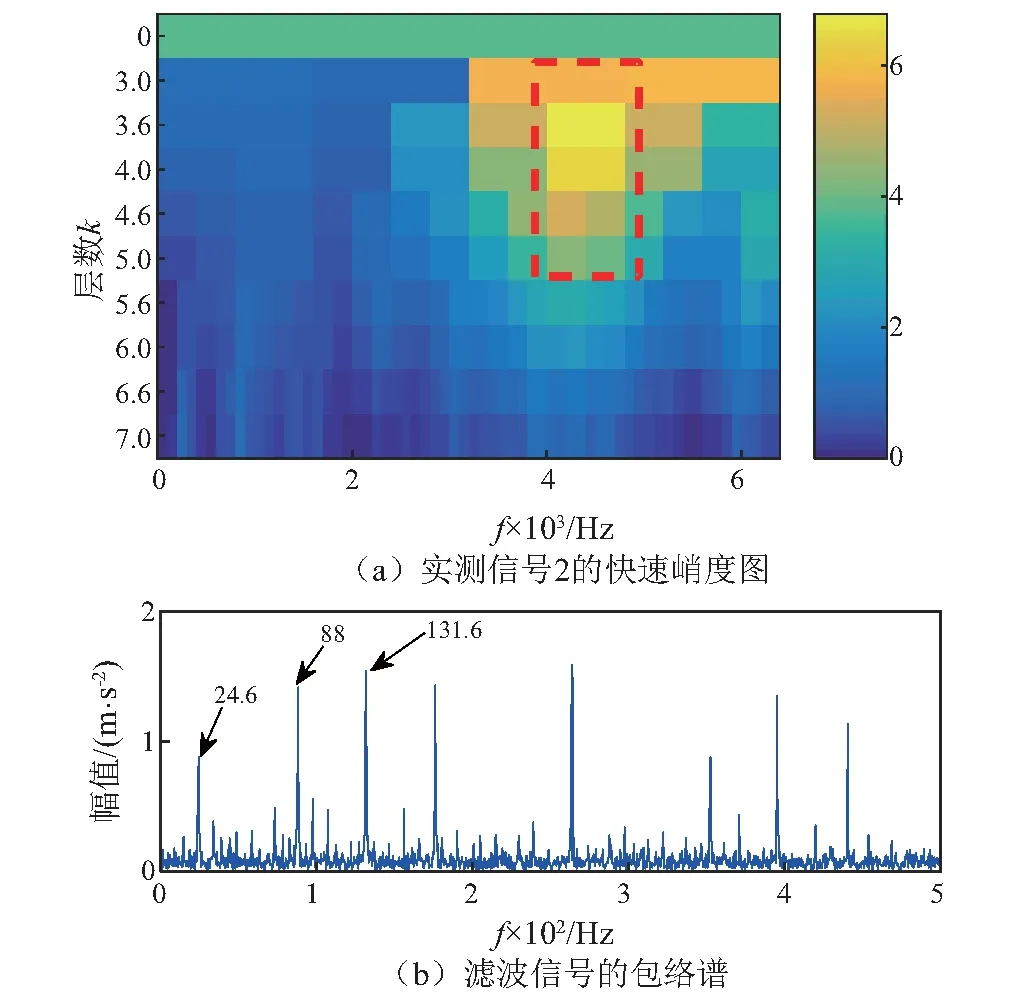
图11 快速谱峭度方法对实测信号2的分析结果Fig.11 Analysis results of measured signal 2 by fast kurtogram
4 结 论
本文基于相关峭度能充分考虑故障信号中所含设定周期冲击成分的特点,提出了基于相关峭度共振解调的滚动轴承复合故障特征分离方法。并应用于不同能量的多共振频带滚动轴承内、外圈复合故障仿真模型,验证了共振频带选择的准确性。通过不同载荷下的轴承内、外圈复合故障实测信号分析表明,该方法受较大能量频带的影响较小,能准确定位出各故障的占优共振频带,实现轴承复合故障的分离。在实际工程中具有一定的应用价值。

