广义解调算法中能量因子的引入与配置原理的研究
刘东东 程卫东 温伟刚


摘要:广义解调算法在振动信号时频谱应用中效果显著,而在分析解调频谱时对频率的初始值非常敏感。提出了能量因子可调的广义解调算法,将其应用到轴承振动信号的处理中并进行有效性评估。为获得轴承信号的相位函数,使用峰值搜索算法在包络信号中检测瞬时故障特征频率,估计拟合函数;引入了能量因子的概念,根据拟合函数配置能量因子,按照提出方法对原始信号进行重构;参考能量因子对重构信号的相位函数进行估计;对重构信号进行解调,得到关于能量因子的解调信号。根据特征频率的解调值与通过测得转速计算的理论值进行对比,评价能量因子配置的合理性。仿真和实测信号的处理,证明了算法的有效性。
关键词:故障诊断;滚动轴承;特征频率;广义解调;能量因子
中图分类号:TH165+.3;THl33.33 文献标志码:A 文章编号:1004-4523(2020)01-0213-06
DOI:10.16385/j.cnki.issn.1004-4523.2020.01.024
引言
滚动轴承在旋转机械设备中起到了极其重要的作用,但是常处于变载荷、变转速等恶劣工况下容易损坏,因此对其故障诊断非常重要。轴承出现故障时,故障点与滚动体的碰撞会引起一系列冲击。这些冲击不仅会激起机械部件或系统的共振,还会调制信号的振幅。因此,轴承故障冲击信号可以看成固有频率作为载波频率,故障特征频率作为调制信号的调幅信号。共振解调技术可以对信号进行解调,但是该算法的应用要求转速平稳。实际工况中设备的频繁启动或负载变化等因素,都会引起转速波动。当转速波动时,调制特征更为明显,信号包含更丰富的故障信息。因此,如何从转速波动下的信号获得故障特征具有重要研究意义。
广义解调时频分析算法可以将时频分布为倾斜、非线性的瞬时频率转换成平行于时问轴的瞬时频率。由于非常适用于处理非平稳的调幅一调频信号,已经开始应用于轴承和齿轮信号的处理。文献[5]使用广义解调时频分析,将齿轮振动信号分解为若干个单分量信号,再对瞬时频率信号重采样,进行包络分析,提取齿轮故障特征。文献[6]利用多尺度线调频基稀疏基对齿轮振动信号进行分解,估计相位函数,对信号解调得到齿轮的故障特征频率。文献[7]将广义解调算法应用于轴承故障诊断,有效地从振动信号中解调出轴承故障特征。文献[8]将迭代广义解调算法应用于行星齿轮箱的故障诊断中,改善了时频谱的可读性。广义解调算法无论在处理齿轮还是轴承信号时,都是将瞬時频率的能量解调到初始频率,因此解调精度对初始频率非常敏感。如果相位函数是通过估计获得,这就要求瞬时频率初始值的拟合精度非常高。
基于时频表达的瞬时频率估计算法是最常用的提取频率方法。例如短时傅里叶变换、小波分析等常用时频分析方法,时频分辨率受Heisenberg不确定性原理的限制;Wigner-Ville变换虽然分辨率较高,但是受到交叉干扰项的限制。针对这些问题,文献[11]提出Synchrosqueezed Wavelet Trans-form算法,通过压缩小波时频分析结果,有效提高了时频分辨率。但是,时频分辨率的提高,必然增加计算负担。而且要想将基于时频谱获得的瞬时频率用于估计相位函数,必须要求瞬时频率具有连续性。
然而,在低频位置故障特征频率幅值较小,更容易受到噪声污染。如果使用估计相位函数直接对信号进行解调,解调频率误差很大。试图提高时频分辨率来提高拟合精度,不仅会使效率降低,而且不能保证低频位置的精度。为此,本文引入能量因子的概念,根据处理信号的特点,通过自动调整能量因子的大小,设置解调位置。将其应用于轴承信号处理,进行有效性的检验。
1能量因子可调的广义解调
当轴承发生故障时,随着轴承转动,在时域信号中会形成一个冲击序列,激起了机械系统的高频共振。冲击序列还会不断的调制共振频率形成故障特征频率。当转速恒定时,故障特征频率及其谐频,在包络时频谱中应该表现为平行于时问轴的直线。理论上滚动轴承的故障特征频率与转速成线性关系,当转速变化时,每个时刻的故障特征频率也会与转速趋势保持一致。而每个时问点的故障特征频率称为瞬时故障特征频率。从能量的角度分析,当转速变化时,故障特征频率的能量已经不再集中于某一频率处。因此,转速的波动使包络频谱出现频率模糊的现象。为了能更精确地估计瞬时故障特征频率,提高瞬时故障特征频率趋势线拟合精度,使用幅值重调的峰值搜索算法对其进行估计。当转速较低时,由故障引起的冲击相对较小。而且当转速较低时,瞬时频率更容易受到噪声的污染。因此,对信号进行解调时,一定要弱化转速较低位置拟合频率的影响。
如果可以使用广义解调算法自动将轴承特征频率的能量集中于拟合频率精度较高的一点,那么解调的精度将会随之提高。为此,提出了能量因子的概念。将特定瞬时频率经过解调后,在时频谱中的纵坐标位置称为能量因子。反之,根据解调频率的特点,通过调整能量因子可以控制解调频率的位置。将其应用于瞬时相位估计的广义解调算法中,具体的推导步骤如下:
因此,经过解调可以将x(t)的瞬时频率的能量都集中在能量因子fe。
2能量因子可调广义解调在轴承振动信号处理中的应用
轴承转速波动较大时,瞬时故障特征频率在包络频谱中出现频谱模糊现象。然而,很多设备处于变转速的工况,而且当转速波动时,频率调制更加明显,使得信号中包含更丰富的故障信息。因此,如何实现时变工况下振动信号的解调非常关键。
轴承转速较低时,故障引起的冲击幅值较小,更容易受到噪声的污染。另外,当转频较低时,特征频率谐频的幅值可能会高于基频。因此,估计瞬时频率在低频位置的精度一般较低。幅值重调的峰值搜索算法虽然能提高估计瞬时特征频率的精度,但是轴承低频位置依然存在不可避免的拟合误差。能量因子可调的广义解调算法能通过自适应地调整能量因子,最大程度地弱化低频的拟合误差对解调精度的影响。旋转机械故障引起冲击的幅值随着转速的增大而增强。轴承转速较高时,特征频率在包络时频谱具有较高的幅值,估计的精度会更高。因此,在估计相位函数时,能量因子自动设置为转速最大时刻对应的瞬时频率。
基于能量因子可调广义解调的轴承故障诊断算法的具体步骤如下:
(1)对原始信号x(t)进行Hilbert变换和短时傅里叶变换,获得包络时频谱;
(2)使用幅值重调的峰值搜索算法在包絡时频谱中提取瞬时故障特征频率,对其拟合得到拟合函数f(t);
(3)根据拟合函数f(t)自适应地配置能量因子,对原始信号x(t)进行重构;
(4)利用拟合函数,参考能量因子值对重构信号的相位函数进行估计,依据x1(t)和x2(t)的估计频率f1(t)和f2(t)计算相位函数v1(t)和u2(t);
(5)对重构信号进行Hilbert变换得到解析信号y1(t)和y2(t),对解析信号进行解调d1(t)和d2(t);
(6)对d1(t)和d2(t)进行Hilbert变换得到解调信号z1(t)和z2(t),对解调信号z1(t)和z2(t)进行重构得到z(t),对z(t)进行Fourier变换得到解调频谱。
3仿真分析
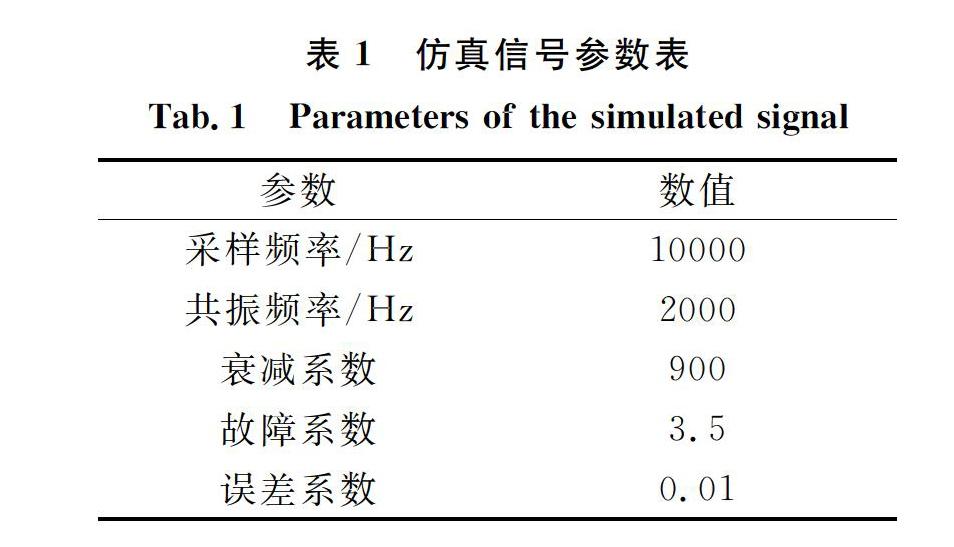
为了验证算法的效果,构造时变工况下轴承振动信号的仿真模型x(t)为
图1为仿真信号的时域波形,波形幅值与转速变化趋势基本相同。对仿真信号进行Hilbert变换得到包络信号。对包络信号进行傅里叶变换得到如图2所示的包络频谱,可以看到由于转速的变化使得包络频谱出现模糊现象。仅仅依靠该包络频谱,无法判断轴承的运行状况。
使用幅值重调的峰值搜索算法估计的瞬时故障特征频率如图3所示。拟合值与计算值基本一致。根据估计的瞬时故障特征频率计算相位函数,使用广义解调算法与能量因子可调广义解调对瞬时故障特征频率进行解调,得到的解调频谱如图4所示。广义解调频谱在频率15.9Hz处出现了峰值。理论计算的频率为3.5×5.85=20.5Hz,处理误差为4.6Hz。能量因子可调广义解调算法解调的频谱在209Hz出现幅值,理论出现幅值的位置3.5×60=210Hz,误差仅为1Hz。因此,提出的算法解调精度相对较高。为了验证能量因子配置方式的合理性,对能量因子设置不同频率值,图5为能量因子各时问对应频率值的解调误差。可以看出在频率较低位置,尤其是在初始值位置,解调误差非常大,而频率较高时,解调的精度也相对较高。
4实验验证
为了进一步验证算法的有效性,使用振动试验台测得滚动轴承振动信号进行处理。试验台和轴承如图6和7所示。在测振动信号的同时,使用编码器采集转速脉冲信号。被检测轴承的外圈和内圈故障特征系数Co=2.55和Ci=4.45,采样频率24000Hz。根据编码器的参数以及转速脉冲测得轴承转速。
图8为外圈轴承振动信号。图9为使用幅值重调的峰值搜索算法在原始信号经过Hilbert变换和STFT得到的包络时频谱中提取得到的瞬时故障特征频率。图10为广义解调算法和能量因子可调广义解调获得的解调频谱。使用广义解调算法得到的解调频率为78.62Hz,理论计算的频率应该为C。×15.35=39.14Hz,解调误差为39.48Hz。提出算法解调频率为139.5Hz,理论计算值为Co×55.0=140.25Hz,解调误差较小。图11为能量因子设置不同频率时的解调误差,从该图可以看出,当能量因子设置较高频率时解调误差较小。因此,对于外圈信号的处理,证明该算法的有效性。
图12为内圈轴承振动信号。图13为使用幅值重调的峰值搜索算法在包络时频谱中提取的瞬时故障特征频率。图14为广义解调算法和能量因子可调的广义解调得到的解调频谱。广义解调算法的解调频率为105.4Hz出现幅值,理论计算的频率应该为Ci×20.01=89.25Hz,解调误差为16.15Hz。提出算法解调频率为245.5Hz,理论计算值为Ci×55.29=246.1Hz,解调误差较小。图15为能量因子设置不同频率时的解调误差,从该图可以看出,当能量因子设置较高频率时解调精度较高。因此,对于内圈信号的处理,证明该算法的优势。
5结论
(1)滚动轴承的瞬时故障特征频率在低频位置幅值相对较小,受噪声影响更明显。广义解调算法可以实现对瞬时故障特征频率的解调,但是通过对仿真和实测信号的处理证明了该算法对相位函数非常敏感。
(2)引入了能量因子概念,提出了能量因子可调广义解调算法,该算法根据信号频率的特点通过调整能量因子,将瞬时频率的能量有目的地调制于能量因子的位置。
(3)在处理轴承冲击信号时,一般高频处的频率拟合误差较小,因此,使用能量因子可调广义解调算法处理轴承信号时,将能量因子自动设置为瞬时频率最大(或较大)值,提高解调精度。
(4)能量因子可调广义解调算法相比于传统的广义解调算法相位函数构造方式,对瞬时频率初始值不敏感,提高了解调精度。
需要指出的是,论文主要研究了能量因子的定义方式以及配置原理,通过仿真和实测信号的处理证明了能量因子配置的合理性,但是在处理最高频率处于端点位置的时候,由于相位拟合函数可能在此处拟合误差较大,因此,能量因子不宜设置端点位置,宜为中问瞬时频率较高的位置。

