稳定器作用下坦克行进间炮口振动特性研究
陈 宇,杨国来
(南京理工大学 机械工程学院,南京 210094)
坦克具有良好的越野性能,坦克行进时,车体(包括火炮)随着地面的起伏而振动,严重影响炮手对目标的捕获和瞄准,使得行进间射击的命中率不高。而坦克稳定器是坦克行驶中自动将炮膛轴线保持在赋予的空间角位置并能瞄准的一种控制系统,是现代坦克火控系统的重要组成部分,能有效提高坦克行进间射击的命中率[1]。目前,对于坦克稳定器的研究较多,但主要着重于稳定器控制方法的研究,Gao等[2-4]分别基于自抗扰控制、模糊控制、鲁棒控制方法建立了坦克稳定器控制系统,研究了其对坦克行进间稳定精度的影响,研究中一般会对坦克动力学模型进行简化,将其看作一个线性传递函数。事实上目前火炮稳定器设计时一般将火炮作为线性系统,认为炮口振动情况与摇架完全相同,因此为控制系统提供系统输入的角度陀螺仪及角速度陀螺仪都安装在摇架上,其稳定目标是摇架。但由于身管柔性及其与衬瓦间存在间隙等非线性因素影响,即使在坦克稳定器正常工作情况下,坦克行进间炮口振动与预期的稳定精度仍存在较大差异,当坦克行驶速度及弹丸出炮口速度不高时,该差异较小。但随着现代坦克对于高机动、高初速和高精度要求的不断提高,这一差异逐渐凸显,不容忽视。
但坦克构造复杂,造价高昂,通过实物样机研究的时间成本和经济成本都较大。目前,虚拟样机技术被广泛运用于武器设计研究的各个阶段,大大降低了坦克的设计和试验成本。大量学者对坦克行进间射击的过程进行了研究,但研究中一般都忽略了坦克稳定器的影响。刘飞飞等[5-6]通过建立身管柔性的坦克行进间发射动力学模型,考虑弹丸动不平衡及质量偏心、弹炮相互作用及间隙,建立行进间弹丸膛内运动方程,获得了弹丸膛内运动规律,分析说明了考虑身管柔性影响有利于获得准确的弹丸起始扰动;徐达等[7]通过建立了考虑身管柔性的坦克全车动力学模型,分析说明了相对于刚性身管,柔性身管模型能有效提高坦克炮射击仿真精度;史力晨等[8]通过状态方程法建立了坦克、火炮系统的振动模型,将系统的动力学响应看作了多刚体系统对地面不平度激励的响应问题,稳定器作用通过刚性系数体现,计算分析了坦克行进间火炮运动规律;金涛等[9]通过建立坦克多刚体模型,采用PID(Proportion Integration Differentiation)控制对坦克火炮进行控制,说明了在坦克高速行驶时,PID控制依然能较好控制火炮振动;Purdy等[10]采用PI控制方法,通过建立某主战坦克高低机电动控制系统的非线性模型,计算发现非线性摩擦会降低控制系统的性能。
目前,关于机电耦合问题的研究已经取得了众多的成果[11]。但目前针对坦克稳定器的机电耦合问题研究还鲜见报道。本文拟采用PID控制方法,在MATLAB/Simulink环境下对坦克垂向稳定器进行复现。通过 RecurDyn/Control模块将建立的动力学模型与坦克垂向稳定器系统相结合,得到完整的机电耦合动力学模型。通过数值计算,分析了非线性因素(身管柔性和身管衬瓦间隙)对稳定器作用下坦克行进间炮口振动特性的影响。此外,文中还重点研究并证实了将炮口高低角位移作为垂向稳定器的控制目标能有效抑制坦克行进间的垂向炮口振动。
1 坦克行进间机电联合建模原理
坦克行进间机电联合建模的主要内容包括坦克系统三维建模、非线性动力学建模、稳定器控制系统建模及接口技术。其中动力学采用RecurDyn建模,控制系统采用Matlab软件的Simulink模块实现,联合仿真的平台为RecurDyn/Control模块。图1为机电联合建模的框架图。

图1 坦克行进间机电联合建模框架图Fig.1 Electromechanical coupling modeling of tank on the move
建模难点在于实现动力学模型与控制系统的实时数据交换。本文利用RecurDyn完成坦克系统的动力学建模,并生成Simulink能够识别的被控制模块,在Simulink中建立稳定器控制模型,利用RecurDyn/Control工具箱实现机电一体化联合计算时的实时双向数据传输,图2所示为其工作原理。机械系统通过RecurDyn解算器进行计算,控制系统通过控制软件解算器进行计算,两者之间通过状态方程联系,在每个固定的取样时间步内都会进行一次数据交换,当取样时间足够小时,可以近似认为在单个取样时间内,系统不发生变化,即近似认为数据交换是实时的。
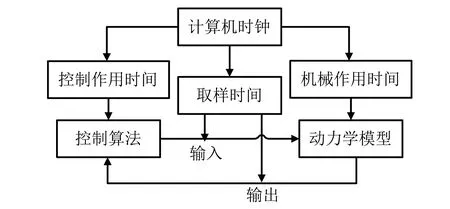
图2 RecurDyn/Control工作原理示意图Fig.2 Operating principle of RecurDyn/Control
2 坦克系统动力学模型
本文建模时暂只考虑坦克垂向稳定器作用,故在此主要分析坦克系统火炮高低向运动,图3为运动简图,坦克车体的运动可以用作用于车体质心位置处的垂向运动yp和转动θp表示。当车体发生小范围转动时,耳轴处的运动可以近似用一个垂向运动yt和转动θp来表示,那么耳轴处的垂向位移和垂向加速度可表示为

图3 坦克系统火炮高低向运动简图Fig.3 Kinematic sketch of tank in elevation
yt=yp+θpltp
(1)
(2)
式中:ltp为车体质心位置距离耳轴处的水平距离。
火炮部分受力分析如图4所示。分析时,将动力油缸简化为作用于驱动位置点与炮塔之间的无质量弹簧系统,等效刚度为kd,则驱动位置点轴向力fd可表示为
fd=kd[yd-ltd(θ1-θp)]
(3)
式中:yd为活塞和活塞杆相对油缸壁的移动距离;θ1为火炮绕质心在高低方向的转角;θp为坦克在高低向绕坦克质心的转角。
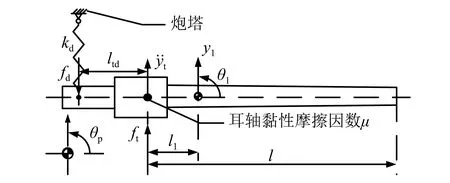
图4 火炮部分受力分析图Fig.4 Stress diagram for part of gun
此外火炮质量为m,其绕质心的转动惯量为I,炮口距耳轴中心距离为l,火炮质心位置距耳轴中心距离为l1,动力油缸在摇架上驱动位置距耳轴中心距离为ltd。火炮在耳轴点所受的垂向作用力为ft;耳轴处等效黏性阻尼为μ。则火炮部分受力分析
(4)
式中:yt为火炮质心处的垂向位移;且其与耳轴存在以下几何约束关系
yt=y1-θ1l1
(5)
(6)
某坦克垂向火炮稳定器[12]是一个电液式自动调整系统,主要由角度陀螺仪、角速度传感器、电子放大器、液压放大器、动力油缸、角速度陀螺仪、火炮等组成。火炮垂向稳定器的结构图,如图5所示。
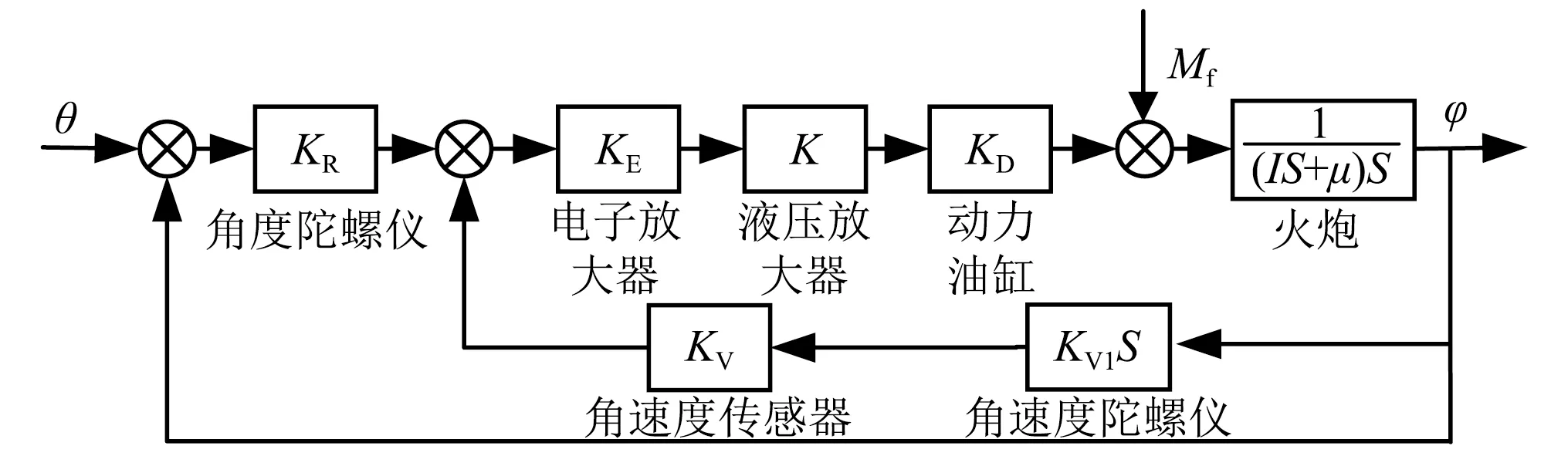
图5 某坦克垂向火炮稳定器结构图Fig.5 Structure diagram of the vertical stabilizer
图5中:KR,KE,K,KD分别为角度陀螺仪、电子放大器、液压放大器、动力油缸的放大系数;I为火炮转动惯量;μ为火炮的黏性摩擦因数;Mf为干扰力矩;KV,KV1分别为角速度传感器和角速度陀螺仪的放大系数;θ为输入;φ为火炮高低角。则垂向火炮稳定器的数学模型可表示为[13]
(7)
式中:G1=KDKKEKR为稳定器对误差角的放大倍数;G2=KDKKEKV为稳定器对角速度陀螺仪内环转角的刚性。
所建立的坦克垂向稳定器系统以摇架高低角位移为控制目标变量,将摇架的实际高低角位移与目标高低角位移(即瞄准角)进行比较产生误差;控制系统通过动力油缸输出控制力,机械系统模型根据输入控制力大小,对摇架高低角位移进行调整,并将角位移信息反馈给控制系统,形成闭环控制。系统有一条前向通路,两个闭合回路,除了角位移反馈回路,还有一个速度反馈回路。在两个回路的协调控制作用下,可维持稳定工况条件下火炮的稳定。
本文选择PID控制来设计坦克垂向稳定器。PID控制是一种线性控制方法,算法表示为[14]
(8)
式中:Kp为比例系数;Ti为积分时间常数;Td为微分时间常数。PID控制的难点在于控制参数的整定,可以根据控制器的参数与系统动态性能和稳态性能之间的定性关系,用试验的方法来调节控制器的参数。
3 坦克行进间机电耦合建模
3.1 坦克非线性动力学建模
如图6所示,该坦克主要包含底盘和火力部分,并以上下座圈相连接。底盘由车体、负重轮、拖带轮、诱导轮、驱动轮和履带板等组成,其他部件质量和惯量通过计算等效至车体上。履带板与地面间为刚性接触。

图6 坦克行进间多体系统虚拟样机模型Fig.6 The multibody system virtual prototype model of tank on the move
火力部分主要包括后坐部分、摇架部分、炮塔部分。身管为模态柔性体,与炮尾通过后端面界面节点固定连接。分别建立身管与前后衬瓦的刚柔接触碰撞[15],并采用非线性弹簧阻尼模型计算其法向接触力f的表达式为
(9)
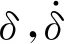
c(δ)=step(δ,0,0,dmax,cmax)
(10)
式中:cmax为法向最大阻尼系数;dmax为最大允许穿透深度。利用c语言编写用户子程序,并利用二次开发功能在软件中插入用户子程序。其它构件简化为刚体,并通过理想约束连接。驻退机和复进机载荷分别通过函数拟合,并直接加载在适当位置。
3.2 三维路面模型
路面不平度是指道路表面相对已知理想基准平面的偏离程度。通过对振动传递路径的分析可以发现,在坦克行驶过程中,路面对左右履带的激励,经过悬挂衰减后传递至车体,经由座圈传递至炮塔,再经过耳轴传递给火炮主体,造成后坐部分的振动,从而影响弹丸运动,造成对射击精度的不利影响,因此建模的要点是准确地重构路面不平度。本文选择采用谐波叠加法基于Mathematica数学工具编写路面谱程序。
将路面空间频率f(f1 (11) 式中:x为路面在X方向上的位移;α为[0,1]上均匀分布的随机数;Ai为中心频率fi对应的谐波的振动幅值 (12) 此外实际行驶过程中,坦克左右履带受到的来自地面的激励并不相同,两侧车轮所受路面激励的相干性可表示为 (13) 式中:dv为轮距;ρ为经验值;n1,n2分别为路面空间频率的上下限。 由于路面不平度函数中的随机相位角α是引起左右履带激励差异的主要因素,因此三维路面不平度随机过程可以表示为 (14) (15) 式中:αx为x方向路面不平度激励的随机相位;αn为新生成的[0,1]的随机数。 根据上式编写三维路面谱程序,重构了长100 m、宽5 m的D级三维路面不平度模型,并通过节点缝合法生成软件可读取的路面文件。 垂向火炮稳定器在坦克行进过程中是通过动力油缸提供火炮的稳定力矩,建模时,忽略动力油缸及相关构件,并通过计算将重量及惯量合并到炮塔及炮尾部分。在耳轴处施加一个反向力矩模拟动力油缸的控制作用,创建输入状态变量,并与反向力矩相关联。设定状态变量为输入变量,设定摇架高低角位移以及PID控制的三个控制参数为输出变量,在RecurDyn/Control模块下导出联合仿真接口文件,在建立好的Simulink控制模型中取代火炮传递函数,构建坦克行进间机械-控制联合仿真系统模型。其中,RecurDyn为主程序,控制系数可直接在主程序中修改。联合仿真系统模型如图7所示。 图7 联合仿真系统模型Fig.7 System model of Co-simulation 火炮稳定精度为坦克行驶在起伏路面上时,火炮摆动振幅的算术平均值,表达式为 (16) 式中:N为采样的总点数;θi为采样得到的火炮高低向角位移。数值计算时,通过给坦克主动轮施加驱动力模拟坦克行驶过程。本文选择对坦克以20 km/h速度行驶在D级路面上时的炮口振动进行计算分析。由于前4 s坦克处于速度不稳定状态且建模时仅考虑了垂向稳定器,因此在分析时仅分析4 s后炮口高低向振动规律。 目前,在设计坦克垂向稳定器时,一般不考虑非线性因素影响,即认为炮口高低角位移与摇架高低角位移相同,为了证实本文所建立坦克高速行进间联合仿真模型中控制方法的可行性,分别计算了考虑和忽略稳定器作用时坦克行进间摇架处振动情况。 由图8可知,不考虑稳定器作用时,摇架处的高低振动幅值最大为11.69 mrad,显然,在此条件下难以完成准确射击并命中目标的动作。而稳定器控制作用后,通过控制系数调整,摇架高低角位移得到了有效控制,其最大幅值显著减小至3.01 mrad,最终能够保证稳定精度约0.98 mrad,而根据朱竞夫等的研究可知目前火炮垂向的稳定精度约为0.52~1.05 mrad,这说明计算结果能满足实际稳定精度要求,说明了控制方法具有可行性,也间接验证了所建机电耦合模型的准确性。 图8 坦克行进间摇架高低角位移Fig.8 Vertical cradle angular displacement of tank on the move 坦克实际行驶过程中,后坐部分构件柔性及构件间碰撞等非线性因素是现实存在的,为了分析这些非线性因素对于炮口高低角位移的影响,本文选择在机电耦合模型中考虑身管柔性及身管衬瓦间隙两个最显著的非线性因素,计算了此条件下坦克行进间摇架和炮口振动响应。同过对控制参数进行调整,得到摇架和炮口振动的振幅比较,如图9及表1所示。 图9 摇架和炮口高低角位移对比Fig.9 Vertical angle displacement comparison between muzzle and cradle 表1 摇架和炮口高低角位移比较Tab.1 Vertical angle displacement comparison between muzzle and cradle 由图9可知,坦克行进间摇架处和炮口高低角位移差别很大,由于身管自重的原因,再考虑身管柔性因素后,身管会发生向下的弯曲,在图9中体现为炮口高低角位移较摇架处整体偏小。但两处高低角位移的曲线波形几乎一致,这说明当坦克在较平坦路面以较低速度行驶时,路面激励还是影响炮口及摇架处高低角位移的主要因素。由表1可知,炮口处稳定精度为3.36 mrad较摇架处的0.98 mrad增大了241.49%;炮口高低角位移的标准差为1.26 mrad较摇架处的1.13 mrad增大了11.11%。这说明考虑身管衬瓦间隙和身管柔性这两种非线性因素后,炮口振动高低角位移显著大于摇架处,同时炮口高低向振动振幅也大于摇架处。 通过以上分析可知传统稳定器设计过程中的假设与实际并不相符,因此,按照传统方法设计的稳定器,不可避免的存在一定误差,身管衬瓦间隙和身管柔性这两种非线性因素会严重降低了坦克垂向稳定器的稳定效果,显然,这不利于提高坦克行进间射击精度,需要针对这一问题进行更深入的研究。 图10给出了坦克行进间摇架和炮口高低角位移频域图,图11给出了坦克稳定器稳定力矩频域图,由图可以看出,三条曲线的主峰值对应的频率都为0.87 Hz,其与坦克车体自身频率相近,因是由坦克车体振动造成的,其第二峰值对应的频率都为17.62 Hz,与身管一阶模态频率相近,应是由坦克炮身管弯曲造成的。此外由图10中局部放大图可以看出炮口处高低角位移频域图的第三峰值约为39.20 Hz,这与由图12给出的前衬瓦与身管接触力频域图主峰值对应的频率相近,应是由坦克炮身管衬瓦接触造成的。因此,在坦克行进过程中,车体振动对于炮口高低角位移的影响依次大于身管弯曲和身管衬瓦接触影响。同时,坦克行进间炮口高低角位移频域图中的高频信号明显强于摇架处高低角位移频域图,这同样是由身管衬瓦接触及身管柔性这两种非线性因素造成的。 图10 摇架和炮口高低角位移频域图Fig.10 Frequency range chart of the vertical angle displacement of muzzle and cradle 图11 稳定力矩频域图Fig.11 Frequency range chart of stabilizing moment 图12 前衬瓦与身管接触力频域图Fig.12 Frequency range chart of contact force between the front bushing and the barrel 目前,在设计坦克垂向稳定器时,一般不考虑身管弯曲和身管衬瓦间隙(即身管为刚性体,身管与摇架简化为滑移铰连接),此时炮口高低角位移与摇架高低角位移相同,选择摇架处的高低角位移作为控制系统输入,即控制目标为摇架的高低角位移,由上文分析可以发现,由于非线性因素的影响,炮口振动位移幅值显著大于摇架位移幅值,且炮口处于高频振动状态,显然这不利于控制炮口振动,提高坦克行进间射精精度。针对这一问题,本文尝试将坦克垂向稳定器的控制目标改为炮口处的高低角位移。 在建立的机电耦合动力学模型中,通过位移函数导出炮口处垂向角位移,再利用M文件将其导入到建立的垂向稳定器控制模型作为模型的系统输入。而在实际坦克中可通过在炮口处安装电涡流位移传感器测量炮口垂向位移,并通过计算后传递至稳定器作为输入。 对坦克以20 km/h速度行驶在D级路面上时的炮口振动进行计算分析,得到了稳定器控制结构改进后的炮口垂向角位移,如图13所示。由图13可知,炮口处的高低摆动振幅的极值由原稳定器控制结构情况下的14.11 mrad减小为0.91 mrad,减小了幅度达93.55%;稳定精度由3.36 mrad减小为0.26 mrad,减小幅度达92.21%,说明控制结构改进对于提高稳定精度效果明显。综合以上可以得出,稳定器控制结构改进对于减小炮口振动幅值有很好的效果,这有利于提高坦克行进间的射击精度。 图13 坦克行进间炮口高低角位移Fig.13 Vertical muzzle angular displacement of tank on the move 本文基于RecurDyn/Control模块将建立的考虑多个非线性因素的坦克行进间刚柔耦合动力学模型与坦克垂向稳定器系统相结合,得到完整的机电耦合动力学模型。通过数值计算对坦克在稳定器作用下的行进间炮口振动特性进行分析,结果表明在坦克行进过程中,车体振动是影响炮口高低角位移最主要因素。坦克垂向稳定器能有效减小坦克行进间摇架和炮口处的垂向振动。但身管柔性及身管衬瓦间隙造成炮口处高低角位移仍远大于摇架处高低角位移,显然这不利于保证行进间射击精度。为了有效减小炮口垂向振动,提出了改进垂向稳定器控制目标为炮口处高低角位移的方法,通过数值计算证明方法能有效减小坦克行进间炮口高低角位移,有利于提高坦克行进间射击精度。但本文研究中未考虑动力机构的建模,而是采取直接控制的手段,所建模型与实际情况仍存在一定差异,这将在今后工作中逐步完善。3.3 联合建模

4 炮口振动数值计算与分析
4.1 控制方法可行性分析

4.2 非线性因素影响
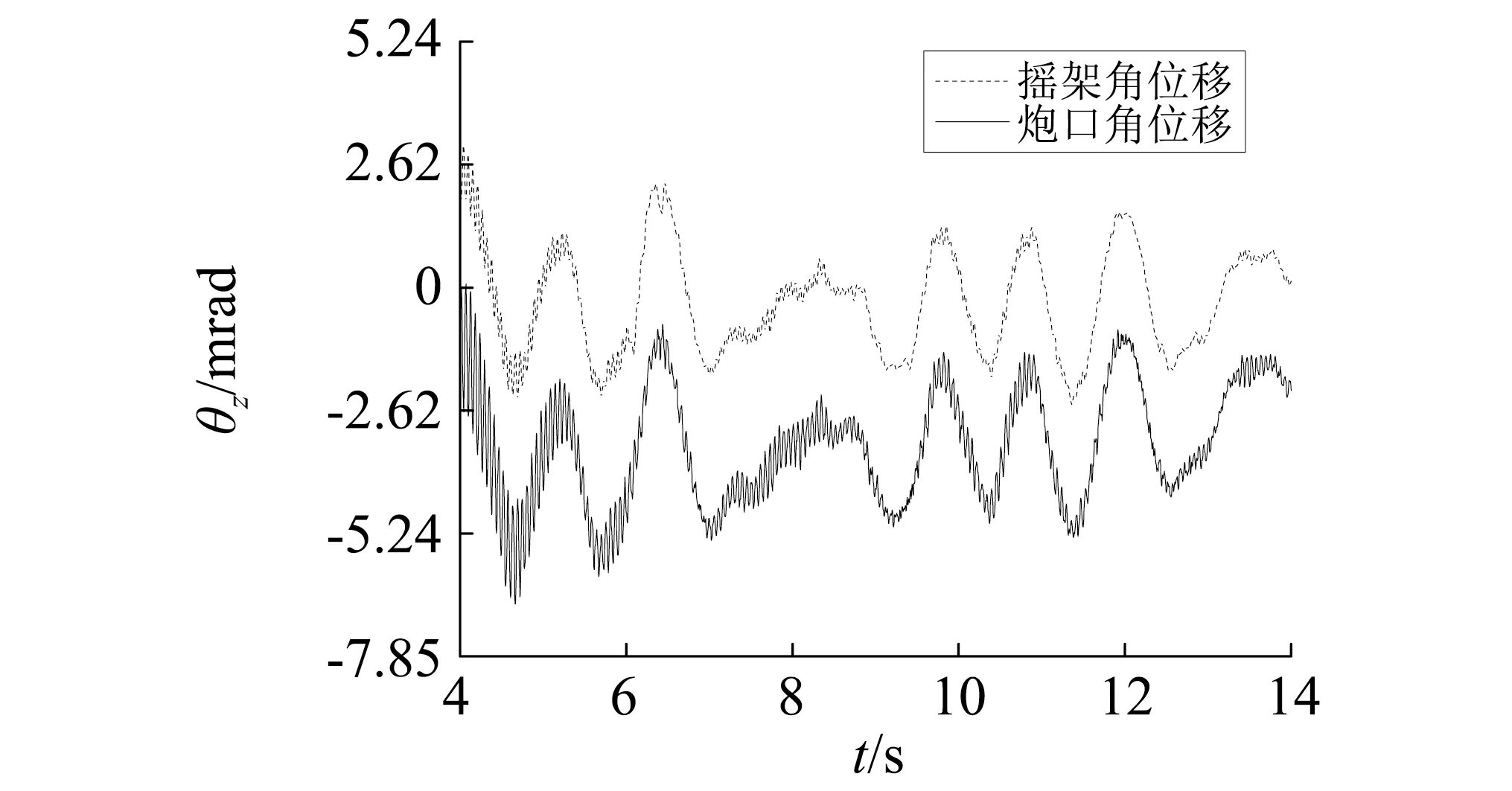
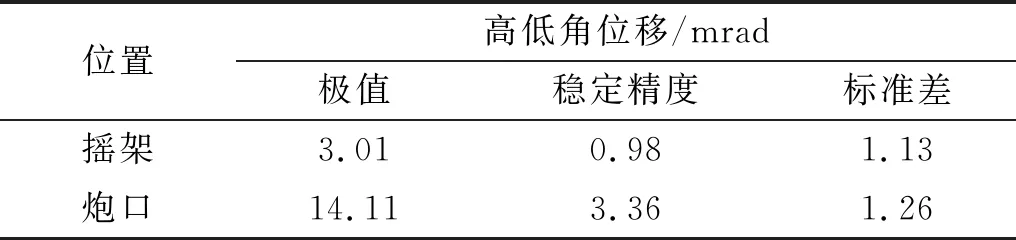


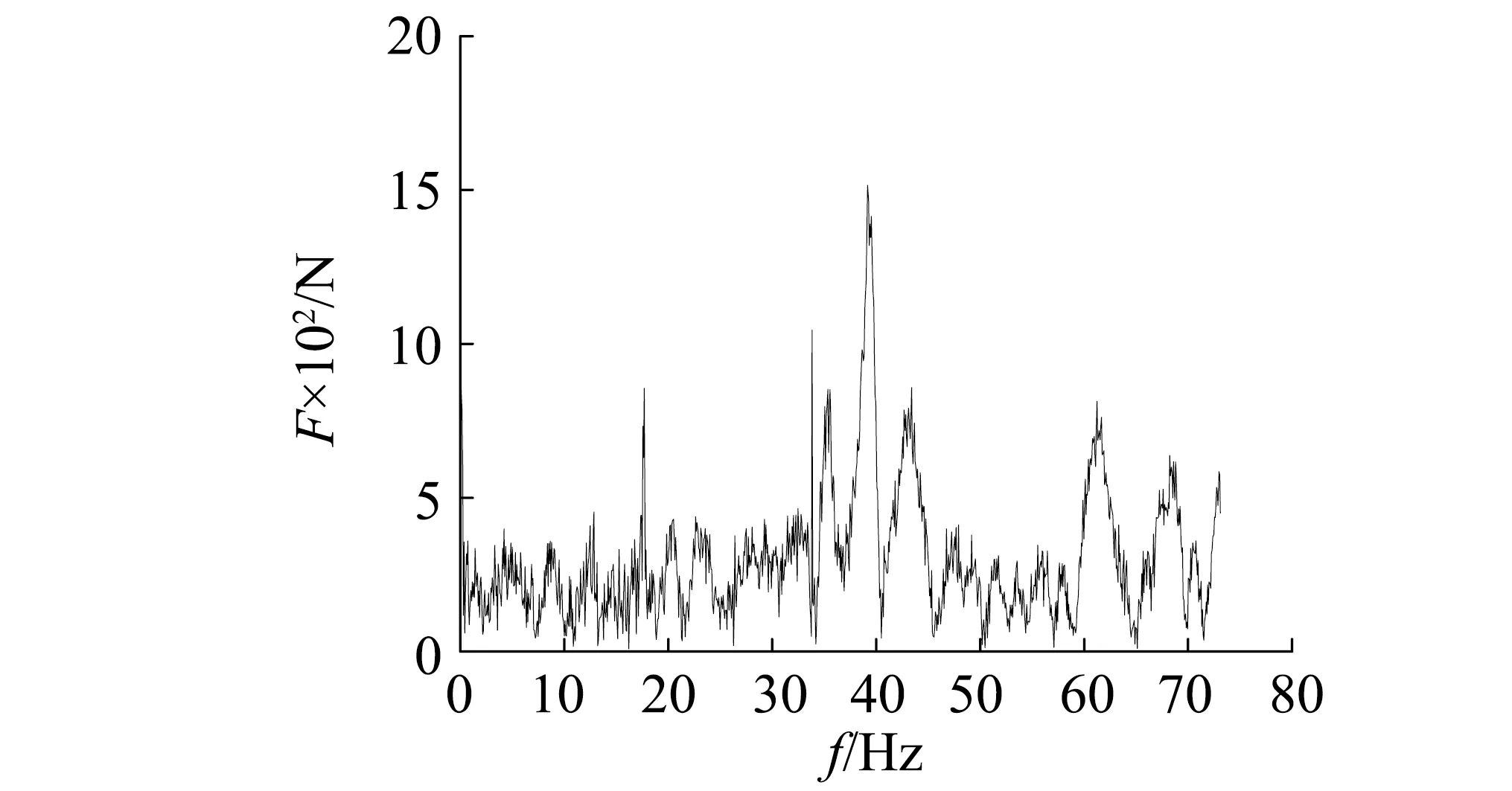
4.3 稳定器控制目标改进
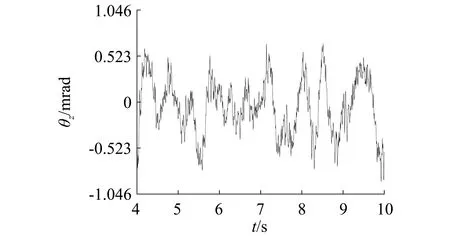
5 结 论

