方形棱柱涡激压力空间相关性研究
朱乐东,陈修煜
(1.同济大学 土木工程防灾国家重点实验室,上海 200092;2.同济大学 土木工程学院,上海 200092;3.同济大学 桥梁结构抗风技术交通行业重点实验室,上海 200092)
现代桥梁结构正向着跨度更大、结构更柔、主梁更纤细的方向发展,这必然导致其对风的敏感性增加。[1]涡激振动是桥梁风致振动的一种形式,但针对桥梁涡激振动现象的研究很少考虑涡激气动力沿跨向的变化以及振幅的影响,实际上,涡脱只有在低雷诺数的范围内才表现为简单的二维流动。Roshko[2]在研究圆柱尾流时发现,随雷诺数的增大,圆柱涡脱会表现出越来越强的三维特性。Berger等[3]又指出在某些情况下,圆柱尾流中往往会出现斜涡脱,即涡管轴线与圆柱轴线间存在大约15°~20°的夹角。Williamson[4-5]在试验中发现斜涡脱沿圆柱轴线方向呈现V字形,指出斜涡脱才是尾流的稳定状态,而平行涡脱只有在旋涡刚刚形成时或是提供特殊的端部条件时才有可能发生。Wilkinson[6]以方柱断面为对象研究了固定方柱、强迫振动方柱两种情况下方柱表面压力的跨向相关特性,得到了方柱表面压力相关系数随跨向距离的变化曲线。目前,在进行桥梁全桥三维涡振分析时一般假设涡激力沿跨向完全相关或采用Wilkinson于1981年通过刚性节段模型强迫振动测压试验得到的方柱涡激压力跨向相关性经验公式。但是,Wilkinson研究得到的方柱涡激压力跨向相关性经验公式有三点不足之处:①试验中的测压点数量非常少,只研究少数特征点上的涡激压力沿跨向的相关性,以特征点的相关性规律代表整个截面相关性规律不合理;②通过振动位移受人为控制的强迫振动试验获得的涡激力非线性和空间相关特性可能无法准确反映实际情况;③采用强迫振动测得涡激压力为总涡激力,不能够将自激力与涡脱力相互分离,因此也就不能研究纯涡脱力的跨向相关性。肖军等[7-9]对宽高比为5的矩形断面与闭口流线型箱梁断面进行了涡激力展向相关性试验研究,发现振幅对相关性影响在锁定区间上升段与下降段影响程度不同。王孝楠[10]通过宽高比为5的矩形和梯形节段模型风洞试验发现涡激力跨向相关系数随振幅增大而增大。孟晓亮等[11-13]对扁平封闭箱梁、中央开槽箱梁断面开展了同步测压测振试验,发现两种断面发生竖向涡振时涡脱强迫力的跨向相关系数要明显差于总动态升力的相关系数。Zhu等[14]研究均匀流场与紊流场中的中央开槽箱梁断面涡激力跨向相关性,发现涡激力一阶与三阶频率成分在振动中占主要地位。本文同样采用同步测压测振试验方法,摒弃强迫振动的试验方法,使试验结果更具有说服力。
有鉴于此,方形棱柱作为经典钝体模型,在现有的试验条件下,开展涡激压力的空间相关性研究,是对Wilkinson1981年刚性节段模型强迫振动测压试验方案的完善,是对由试验数据得到的方柱涡激压力跨向相关性经验公式的验证,有利于进一步揭示涡激共振的机理,对今后三维涡振分析具有重要意义。
1 风洞试验概况
试验采用风洞测压技术获取模型表面压力。风洞测压技术是通过在模型表面打开一系列的微小测压孔洞,安装压力传感器采集断面表面瞬态压力时程的一种试验技术。试验分为弹簧悬挂节段模型在涡激共振情况下和固定模型情况下的两种测压测振试验,主要采用四个激光位移计和八个电子压力扫描阀测量模型的振动响应信号并同步采集表面气动压力信号。
试验模型为方形棱柱,模型的几何外形尺寸为1 700 mm×130 mm×130 mm,中间段为试验段,长度1 235 mm,两侧为非试验段,均为232.5 mm,截面边长为130 mm。模型四面外衣采用2 mm厚有机玻璃制成,中间纵板采用2 mm厚铝板制成。模型上共设置8个测压断面,如图1所示。截面间距为4X,3X,0.5X,0.5X,2X,4X,5X(X=65 mm),通过组合得到不同间距的截面。测压孔布置如图2所示。每个断面共布置测压点60个,整个节段模型总共布置测压点480个,其中1~19号和31~49号为上下表面测点,靠近边角处测点加密;50~60号测点为迎风面测点,20~30号为背风面测点,测点均匀布置。试验在同济大学土木工程防灾国家重点实验室的TJ-2边界层风洞进行,节段模型现场安装如图3所示。
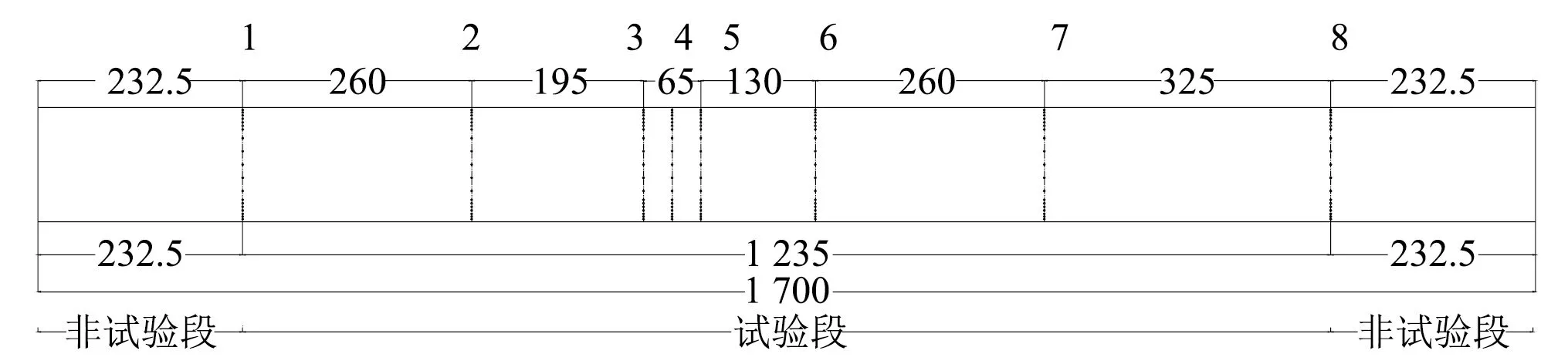
图1 测压断面布置示意图(mm)Fig.1 Arrangement of pressure section (mm)
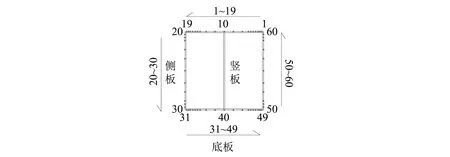
图2 断面测压孔布置示意图Fig.2 Arrangement of pressure taps in the section

图3 方形棱柱弹簧悬挂节段模型图Fig.3 Spring-suspended section model of square prism
试验模型采用8根弹簧悬挂,无附加阻尼时模型竖弯频率为3.71 Hz,试验过程中涡激共振锁定区间的雷诺数Re的范围约为5.5×104~1.9×105。为研究同一折减风速下振动及其振幅对涡激压力跨向相关性的影响,采用调整模型系统的阻尼参数,改变模型涡激共振的幅值的方法,附加阻尼的数值大小变化范围为0.2%~1%。进行弹簧悬挂节段模型测压测振试验时,从零风速开始,逐级增加风速,涡激共振区间内每级风速增量为0.25 m/s。风攻角固定为0°。固定节段模型测压试验所用模型与弹簧悬挂节段模型测压测振试验使用模型相同,将铝制型钢固定在内支架上,然后采用C型夹将模型吊臂固定于铝制型钢上,以实现对节段模型的固定。
2 风洞试验数据处理方法
在沿跨向相关性的研究中,空间相关系数ρ(x1,x2)可以用来描述空间中坐标为(x1,x2)的两点间涡激压力的空间相关统计特征,具体定义为
(1)
式中:x1和x2为节段模型上任意两个横断面上相同编号测点所受的涡激压力时程;ρ为这两个断面上两个测点的跨向相关系数。当x1=x2时,ρ=1.0。
在沿截面相关性的研究中,空间相关系数ρ(i,j)可以用来描述某一断面上编号为i,j的两点间涡激压力的空间相关统计特征,具体定义为
(2)
式中:i和j为节段模型上任意横断面上不同编号测点所受的涡激压力;ρ为该断面上两个测点的沿截面相关系数。当i=j时,ρ=1.0。
3 静止模型测压试验涡激压力相关性
3.1 风速对跨向相关性影响
对于静止模型,气流作用于模型表面的涡激压力仅包括由旋涡脱落直接引起的纯涡脱压力,而不包含非风致附加气动压力及风致振动自激压力等,因此研究静止模型表面涡激压力的跨向相关特性即是研究涡脱强迫压力的跨向相关性。选取迎风面、背风面以及上表面中点进行分析,一方面以上测点具有代表性,迎风面中点为对称模型上下气流分离点,上表面中点以及背风面中点反映漩涡脱落区压力规律;另一方面选取以上几测点可以与Wilkinson的研究进行比较。图4为典型风速下迎风面、背风面与上表面中点纯涡脱压力的跨向相关系数的试验结果。
结果表明:随着跨向间距的增加,相关系数近似按e指数规律迅速从1.0衰减并趋近于零,即方形棱柱节段模型表面的纯涡脱压力沿跨向呈现显著的不完全相关特性。使用e指数函数对其相关系数随间距的衰减规律进行拟合,其中函数的表达形式为
|ρ(ΔX/D)|=e-C|ΔX/D|
(3)
式中:ΔX为跨向间距;D为模型高度;ΔX/D为无量纲跨向间距;参数C为跨向距离增大单位长度时,跨向相关系数的衰减速度。

图4 静止模型纯涡脱压力系数跨向相关性随跨向间距变化曲线Fig.4 Relation between span-wise correlation of vortex-induced pressure and span-wise distance in stationary state
拟合得到的曲线同样绘制于图4中,从中可见拟合曲线与试验数据吻合较好。比较上表面中点与背风面中点各风速下的拟合曲线可见:静止模型上表面中点涡脱压力的跨向相关系数随风速的增加一直增加,而背风面中点涡脱压力的跨向相关系数低风速下随风速增加而增大,在折减风速大于10之后随着风速增大逐渐降低。为了更加直观地体现这一规律,将不同折减风速时相关性衰减规律拟合曲线的拟合系数C绘于同一图中,结果如图5所示。
由图5(a)可知,随着风速的增加,上表面中点纯涡脱压力系数跨向相关性拟合系数C数值缓慢降低,意味着相同间距的两个截面的相关性系数随着风速的增加而增加,这是由于风速增加,上游漩涡脱落对下游测点的影响降低,导致涡激压力系数的离散性降低,因此相关系数较好。静止模型上表面中点纯涡脱压力跨向相关系数的拟合系数C随折减风速增加而减小,数值上远小于背风面拟合系数,即相关性较后者好许多。
由图5(b)可知,背风面中点相关性拟合系数C随折减风速变化呈现两种趋势:当折减风速低于10时,随着折减风速的增加,拟合系数明显降低,体现在相关系数变化规律上为随着跨向间距增大,相关系数衰减的速度变缓;当折减风速高于10时,情况与之前相反,随着折减风速的增加,拟合系数明显升高,体现在相关系数变化规律上为随着跨向间距增大,相关系数衰减的速度变快。
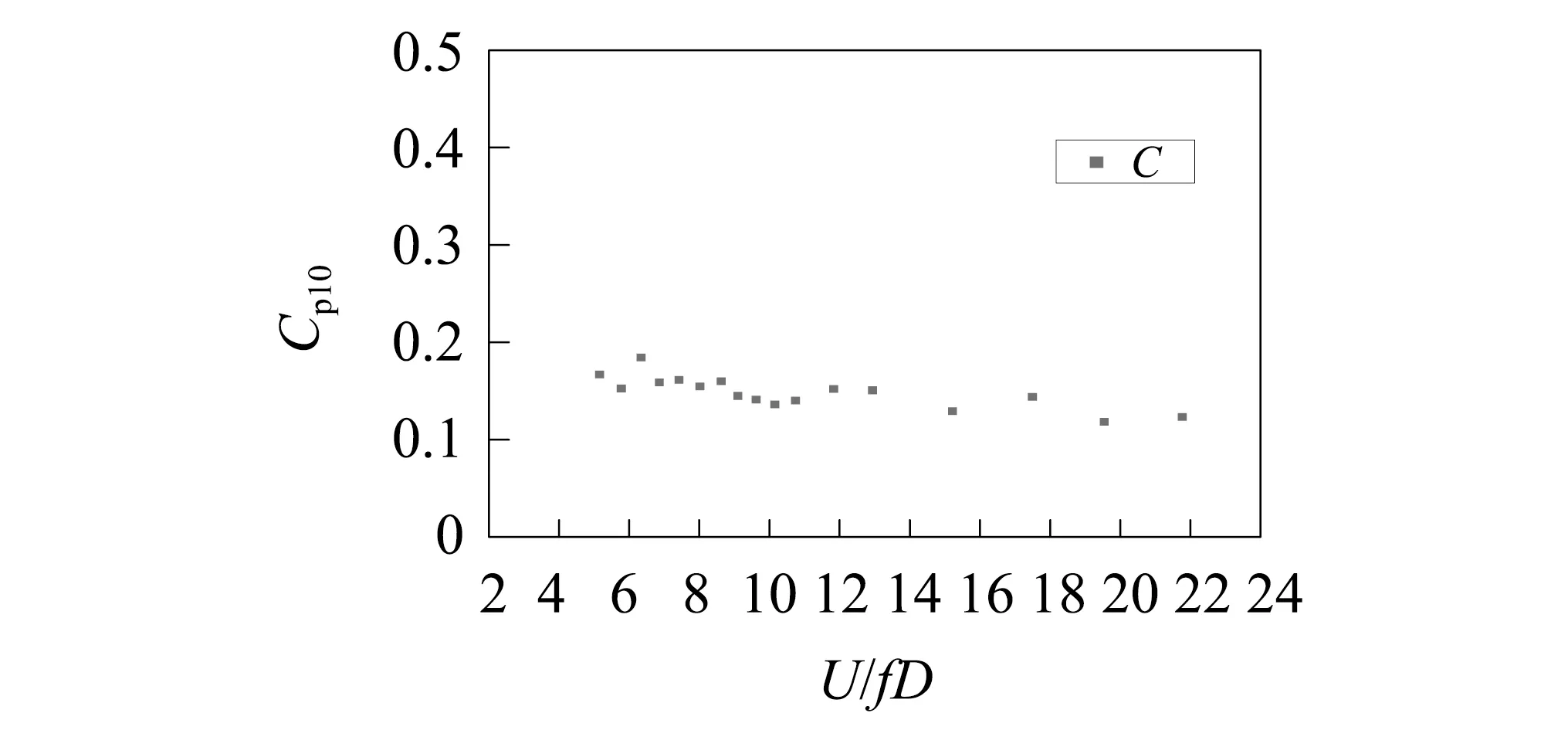
(a)上表面中点
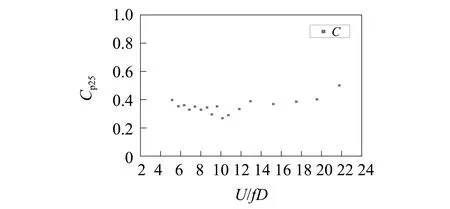
(b)背风面中点
迎风面中点是方形棱柱节段模型上下气流分离点。由图4(c)可知,随着风速的增加,相同间距的两个截面的跨向相关性系数增加;同一风速下相关系数随跨向间距增加几乎不变。迎风面中点相关性规律反映了来流紊乱特性,平均风速增加,脉动风速所占总风速比例降低,压力跨向相关系数增加。
3.2 沿截面周长相关性
为了获得涡激压力沿截面方向相关性变化规律,选取模型上表面中点(P10)作为基准测点,研究同一截面处的其余点与之相关性。图6所示风速为4.39 m/s时,4号截面处不同测点涡激压力相关系数沿截面变化规律。
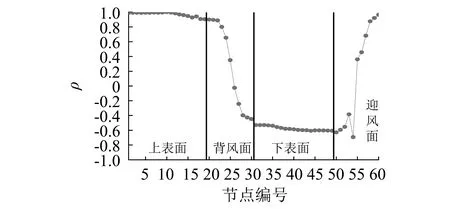
图6 静止模型涡激压力相关系数沿截面变化规律Fig.6 Chord-wise correlation coefficient of vortex-induced pressure in stationary state (based on point 10)
由图6可知,以上表面中点为基准,不同测点与之相关系数的沿截面变化差异明显。上表面(1~19号)测点表现出良好的相关性,其中1~9号测点与10号测点的相关系数接近1.0,11~19号测点相关系数略有下降,但均大于0.9;下表面(31~49号)测点相关性不及上表面,其中31~39号测点与10号测点的相关系数处于0.54~0.6,40~49号测点相关系数约为0.6;背风面(20~30)测点与迎风面(50~60)测点与10号测点的相关性远小于上下表面,尤其在两表面中点处,相关系数较小。
静止模型涡激压力相关系数沿截面的变化规律由漩涡脱落引起,上表面1~9号测点靠近漩涡脱落分离点,受到漩涡脱落的影响较小,相关系数较高,11~19号点位于下游,受到分离区漩涡脱落的影响,相关系数明显小于上游;下表面漩涡脱落规律与上表面相同,但上下表面漩涡脱落不能保证同步,导致相关系数不及位于同一表面的测点;背风面处于尾流区,漩涡脱落引起的气压变化波动大,因此相关系数明显小于上下表面;迎风面中点处于上下气流分离点相关性差,两边由于没有漩涡脱落的影响,因此与上表面中点的相关性也保持较高值。
同时,以上表面中点为基准研究截面各点的相关性,可以明显地发现上下表面压力相关性不够好,差异较大,单以上表面中点相关性规律代替涡激升力相关性规律不够准确。
4 振动模型测压试验涡激压力相关性
4.1 风速对跨向相关性影响
图 7为在涡激共振锁定区间内不同风速下振动模型振幅(Ay)随折减风速(U/fD)的变化关系图。由图可知,涡激共振起振点附近来流折减风速为7.42,此时模型的振动位移约为1.41 mm;随后振幅增加,涡激共振最大振幅为33.84 mm,此时的折减风速为10.16;之后振幅减小,当折减风速为17.49时,振幅约为2.54 mm,涡激共振结束。
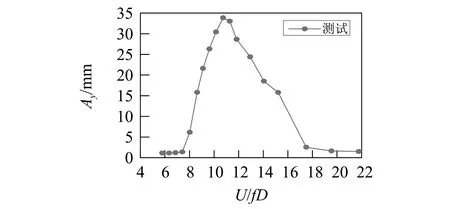
图7 无附加阻尼状态下涡激共振时振幅随折减风速变化曲线Fig.7 Relation between amplitude and reduced wind speed with no-additional damping in resonance
图8(a)显示了振动模型上表面中点涡激压力系数跨向相关性随跨向间距的变化曲线,与图7对比观察整个涡激共振锁定区间可以看出,涡激压力系数的跨向相关系数随着断面间距的增大而降低,且当断面间距达到足够远时呈现出不再变化的趋势。这是因为当距离增大到一定程度时,纯涡脱强迫力已经接近完全不相关,由于节段模型的刚体表面沿跨向以完全一致的步调振动,因此与模型运动状态完全相关的风致自激力与非风致附加自激力是完全相关的,总涡激压力的跨向相关系数趋近于一个常数,可以认为总涡激压力的跨向相关系数随断面间距按下述函数变化
ρ(ΔX/D)=(1-ρ0)e-C|ΔX/D|+ρ0
(4)
式中:ρ0,C为参数,参数ρ0为当断面间距足够远时的涡激压力系数跨向相关系数,参数C为跨向距离增大单位长度时,跨向相关系数的衰减速度。将振动模型涡激压力跨向相关系数的拟合参数随折减风速和相对振幅(Ay/D)变化曲线绘制于图9和图10。

图8 振动模型涡激压力系数跨向相关性随跨向间距的变化曲线Fig.8 Relation between span-wise correlation of vortex-induced pressure and span-wise distance in vibrating state

图9 振动模型涡激压力跨向相关性函数的拟合参数随折减风速变化曲线Fig.9 Relation between fitting coefficient ‘C’ &‘ρ’ of span-wise correlation function of vortex-induced pressure and reduced wind speed in vibrating state
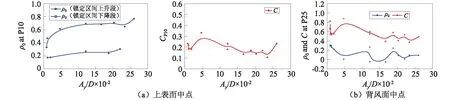
图10 振动模型涡激压力跨向相关性函数的拟合参数随相对振幅变化曲线Fig.10 Relation between fitting coefficient ‘C’ &‘ρ’ of span-wise correlation function of vortex-induced pressure and relative amplitude in vibrating state
对于振动模型上表面中点,对比涡激共振区间内风速振幅曲线,可以发现:涡激共振开始时,模型振动位移刚刚开始产生变化,涡激压力跨向相关系数急剧增加,提高幅度约为0.2,当涡激共振进入最大相对振幅附近风速范围时,涡激压力跨向相关系数达到最大值,锁定区间内振幅下降段相似振幅情况下,相关系数要差于振幅上升段,这可能与气流的变化有关,需要进一步的研究;参数C在相对振幅较小时维持在0.2,在相对振幅超过0.2之后围绕0.2波动。振动模型背面中点相比于上表面中点相关性差,涡激压力跨向相关系数处于0~0.3,参数C处于0.4~0.8,明显高于上表面中点值,即随断面间距的增加相关系数衰减的速度更加快。
对于振动模型迎风面中点,图8(c)显示了其涡激压力系数跨向相关性随跨向间距的变化规律。对比涡激共振锁定区间以及振幅,可以发现:涡激共振起振点以及涡激共振结束点(折减风速为7.42和17.49),振幅较小,跨向相关性变化规律与静止模型相近;共振时涡激压力系数跨向相关系数较静止时明显降低,且具有较大离散性,振幅越大,相关性系数降低越明显,离散程度越大。
4.2 幅值对跨向相关性影响
通过改变振动模型的阻尼参数进而改变幅值的方法,研究相同风速条件下不同幅值对涡激压力跨向相关性影响。试验中使用改变油阻尼器的阻尼片大小的方法改变模型的附加阻尼。要确保不同阻尼情况下存在公共的涡激共振锁定区间,同时相同风速条件下振幅具有明显差异,因此,采用试验风速均为4.39 m/s的4组不同阻尼试验数据,相对振幅分别为0.166 3,0.144 3,0.120 5和0.083 3。选取模型上表面中点为研究测点,将实测数据与相关系数沿跨向拟合曲线均绘于图11中,拟合公式采用式(4)。

图11 涡激共振区间内幅值对模型涡激压力跨向相关系数影响对比图Fig.11 Comparison of span-wise correlation function of vortex-induced pressure with different amplitude in lock-in interval
由此可知,涡激共振锁定区间内,振幅对涡激压力跨向相关性影响显著。当相对振幅为0.166 3时,8倍间距拟合相关系数为0.79,当相对振幅为0.083 3时,8倍间距拟合相关系数仅为0.52。振幅增加会增加风致自激力和静止空气产生的非风致附加自激力成分,振幅增大,两者在总的涡激压力所占的成分增大,因此涡激压力跨向相关性变大。
将Wilkinson试验与本试验中得到的不同相对振幅下压力跨向相关性规律绘于图12可知,两套试验结果各自均显示方柱的涡激压力跨向相关性随着振幅的增加而增强,但是本文通过自由振动试验得到的方柱涡激压力跨向相关系数总体上要小于Wilkinson通过强迫振动试验得到的结果。

图12 Wilkinson试验与本试验中振幅对跨向相关性影响对比Fig.12 Comparison of the influence of amplitude on span-wise correlation in this and Wilkinson’s test
4.3 沿截面周长相关性
与研究静止模型涡激压力沿截面方向相关性变化规律相同,振动模型也选取模型上表面中点(P10)作为基准测点,研究沿着同一截面处的其余点与之相关性。如图13所示,风速为4.39 m/s时,4号截面处不同测点涡激压力相关系数沿截面变化规律。
由图13可知,以上表面中点为基准,振动模型不同测点与之相关系数的沿截面变化规律与静止模型的规律不同。与静止模型相比,振动模型涡激压力不仅由漩涡脱落引起,而且与模型运动时跟空气的相互作用产生的自激压力有关。上下表面自激压力成分大,因此上表面1~9号测点与10号测点的相关系数接近1.0,12~19号测点受分离区漩涡影响相关系数明显下降,在0.7附近波动;下表面有上表面相似的变化规律,其中31~39号测点与10号测点的相关系数处于0.6~0.9,变化较大,40~49号测点相关系数约为0.9;背风面测点与迎风面测点压力方向与运动方向垂直,自激压力成分少,与10号测点的相关性远小于上下表面。
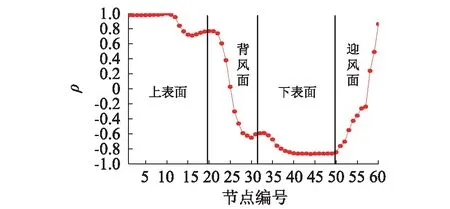
图13 振动模型涡激压力相关系数沿截面变化规律Fig.13 Chord-wise correlation coefficient of vortex-induced pressure in vibrating state (based on point10)
同样,上下表面压力相关性差异较大,单以上表面中点结果代替截面涡激升力相关性规律不够准确。
5 结 论
通过进行方形棱柱节段模型同步测压测振试验,分析了模型表面涡激压力沿跨向和截面的相关性。具体研究结果如下:
(1)方形棱柱静止模型表面的纯涡脱压力跨向相关性较差,跨向相关系数随跨向间距的增大而呈现出按e指数函数衰减至接近于0的规律,且衰减速度随来流风速的增加变化不明显。
(2)涡激共振时,刚体模型沿跨向完全相关的风致非线性自激力和非风致附加自激力会增加总涡激压力的跨向相关特性,因此导致在一定风速范围内,振动模型表面的总涡激压力会表现出较好的相关性,并且其相关性随风速的变化规律呈现出随风速先增强后减弱的现象。此外,涡激压力跨向相关性随振幅增大明显提高。
(3)截面不同测点涡激压力相关性不同,差异较大。使用侧表面中点涡激压力跨向相关性随跨向间距变化规律代替总涡激升力跨向相关性规律不太合适,因此需要采用截面积分方法求得截面总涡激升力,进而研究其跨向相关性。

