非对称П型梁和流线型箱梁气动性能风洞试验研究

李 明，孙延国，李明水，周 强

(1.西南交通大学 桥梁工程系，成都 610031；2.西南交通大学 风工程四川省重点实验室，成都 610031)

随着桥梁建设技术的进步以及环保理念的不断提高，在实际工程中考虑地形的复杂性和经济等因素的情况下，有时会将桥梁主梁断面设计成为非对称形式，例如杰拉德达斯蒙德桥(美国)、霍洛加兰桥(挪威)以及跨湾连接路桥(香港)等。这些桥梁都只设置了一个单边人行道，因此主梁横断面均表现为非对称。与对称形式的主梁断面相比，非对称主梁可以很好地利用空间资源，经济性能也相对较好。

大跨度桥梁由于结构轻柔且阻尼比较小，对风荷载的作用十分敏感，因此主梁的气动性能成为桥梁设计过程中考虑的重要因素。影响主梁气动性能的因素包括主梁的气动外形、来流攻角和风向角以及雷诺数等[1-3]。其中主梁的气动外形是重要的影响因素，主梁上的风嘴、栏杆以及气动措施等都会对主梁的气动性能构成重要影响。孟晓亮等[4]通过风洞试验和数值模拟研究了风嘴角度对封闭和半封闭箱梁涡振和颤振性能的影响，并发现采用较尖的风嘴可以改善此类主梁断面的涡振性能，且基本不会对颤振稳定性产生不利影响。管青海等[5]通过表面压力同步测量，研究了栏杆对箱梁断面涡振特性的影响，发现栏杆使上表面的来流分离更加严重，改变了上表面的压力系数均值和上下表面的脉动分布，但对下表面的压力均值不产生影响。陈政清等[6-7]根据理论分析、数值模拟以及流迹显示试验研究了中央稳定板提高桁架梁悬索桥颤振稳定性的气动机理，发现中央稳定板降低了气动负阻尼，并增加了弯扭耦合程度，降低了颤振频率，从而提高了主梁的颤振临界风速。夏锦林等[8]基于节段模型风洞试验和CFD(Computational Fluid Dynamic)数值模拟，研究了双开槽箱梁断面的颤振和涡振性能，发现防撞栏杆基座对颤振稳定性影响较大，中央稳定板可以有效提高颤振临界风速，纵向间隔的纵向格栅能很好地抑制涡振。桥面上的车辆也会对主梁的气动性能产生一定的影响，周立等[9]利用节段模型试验研究了栏杆、汽车等对汽车-主梁桥面系统的气动三分力系数的影响。李永乐等[10]研究了桥上车辆对板桁主梁以及双层铁路钢桁桥气动性能的影响，发现桥上车辆的存在显著改变了主梁的气动特性。既有桥梁会对其邻近新建桥梁主梁的气动性能产生一定的干扰效应，包括三分力系数、涡振、颤振性能等[11-13]。此外，叶献辉等[14]以一对耦合控制面结构的气动弹性模型为研究对象，分析了结构在不同耦合刚度下非对称参数对颤振速度影响的变化规律。Hu等[15]利用风洞试验、激光多普勒风速测量及流迹显示试验对垂直来流风向的非对称柱体(非对称倒圆角柱)旋涡脱落进行了研究，发现随着非对称倒圆角半径的增加，脱落旋涡的尺度也相对变大，且逐渐向柱体尖锐棱角侧发生转移。

目前关于桥梁主梁的气动性能研究，相关文献多为对称形式的主梁断面，而非对称形式的主梁断面气动性能研究鲜有报道。为了研究非对称人行道对主梁气动性能的影响，本文以杰拉德达斯蒙德桥(非对称П型梁)和霍洛加兰桥(非对称流线型箱梁)为研究背景，在不同来流风向下利用节段模型风洞试验对两种形式非对称主梁的气动性能进行了研究，包括主梁的三分力系数、涡振以及颤振特性。

1 工程概况

杰拉德达斯蒙德桥位于美国加利福尼亚州，该桥为主跨304.8 m的双塔双索面斜拉桥。主梁采用非对称П型叠合梁，桥面宽度为52.0 m。主梁单边设置了一个宽度为3.8 m的人行道。图1为主梁标准断面示意图，图中还给出了风攻角(α)以及来流风向角。

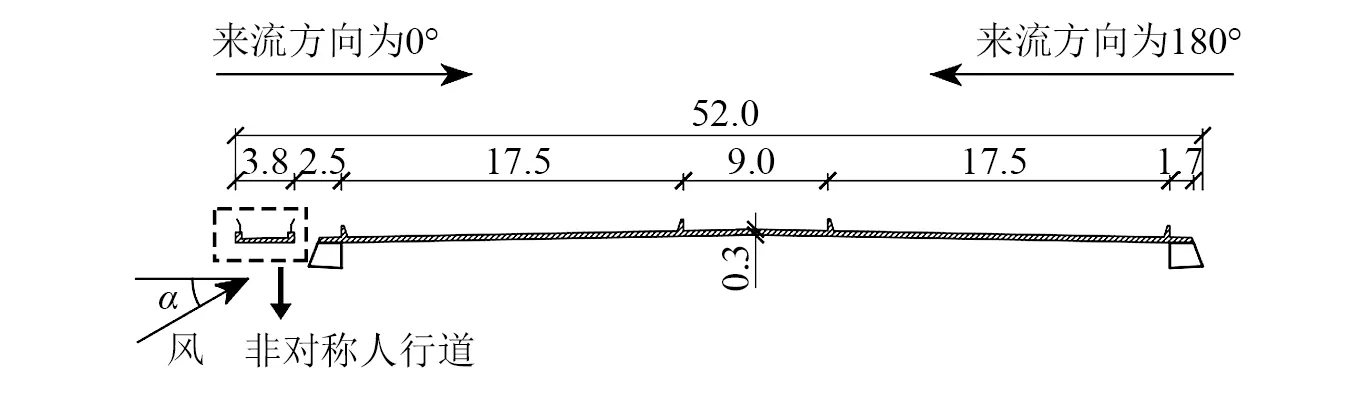
图1 杰拉德达斯蒙德桥主梁标准断面示意图Fig.1 Cross-section of the main girder of Gerald Desmond Bridge

霍洛加兰桥位于挪威的纳尔维克市，该桥为主跨1 145 m的大跨度悬索桥，主梁采用非对称钢箱梁结构，梁高3.0 m，主梁宽度为18.6 m，其中主梁一侧设置了一个宽度为3.6 m的人行道。主梁标准断面如图2所示。

图2 霍洛加兰桥主梁标准断面示意图Fig.2 Cross-section of the main girder of Hålogaland Bridge

2 非对称主梁三分力系数

静力三分力系数为表征平均风作用下结构断面受力大小的无量纲系数，它反映了风对结构的定常作用。在风轴坐标系下，主梁的静力三分力系数可定义为

阻力系数：CD(α)=FD(α)/(0.5ρU2HL)

(1)

升力系数：CL(α)=FL(α)/(0.5ρU2BL)

(2)

力矩系数：CM(α)=FM(α)/(0.5ρU2B2L)

(3)

式中：α为来流攻角；0.5ρU2为气流动压；H,B,L分别为节段模型的高度、宽度和长度。

由图3可知，对于非对称П型梁，当攻角为负时，0°来流风向的三分力系数均小于180°来流风向值，当攻角为正时，0°来流风向的三分力系数均大于180°来流风向值。对于非对称流线型箱梁，当攻角小于-5°时，0°来流风向的阻力系数以及升力系数小于180°来流风向值，而当攻角大于-5°时，0°来流风向的阻力和升力系数大于180°来流风向值，对于升力矩系数，其变化趋势与阻力系数和升力系数相同，只是发生变化的临界攻角为-8°。对比非对称П型梁和流线型箱梁不同来流风向的三分力系数差异可知，除了正攻角的升力系数前者的差值比后者小以外，断面非对称性对П型梁三分力系数的影响要比流线型箱梁显著，这可能是伸出的人行道板使来流提前发生分离，进而使П型主梁周围流场发生变化所致。

(a)非对称П型梁

(b)非对称流线型箱梁图3 均匀流场中非对称主梁断面三分力系数Fig.3 Aerostatic force coefficients of bridge decks with asymmetric sections in the smooth flow

3 非对称П型梁涡振性能

以往研究结果表明[16-17]，主梁涡振性能对主梁的气动外形包括风嘴、栏杆、检修车轨道等构件的形状及位置表现十分敏感。而对于非对称形式的主梁断面，由于布置了非对称的人行道板，其上又附有人行道栏杆，这可能会对主梁的涡振性能造成一定的影响。

为研究不同来流风向非对称П型梁的涡振特性，对非对称П型梁进行了来流风向为0°以及180°的节段模型涡振试验。节段模型缩尺比为1∶45，试验在均匀流场中进行，试验攻角α= 0°，α=±2.5°，α=±5°，风速为0.5～8.0 m/s，控制风速基本步长0.2 m/s，在涡振区采用0.1 m/s步长。需要说明，对于结合梁桥，我国《公路桥梁抗风设计规范》中建议阻尼比取为1%，试验发现大阻尼比条件下(竖向：0.873%，扭转：0.864%)，该节段模型未发生涡激振动，满足相关设计规范[18-19]要求。为了研究该非对称主梁的涡振性能，在小阻尼比的条件下进行了节段模型涡振试验，表1为主要试验参数，图4为风洞中的动力节段模型。涡振试验结果如图5和图6所示(图中数据均已换算到实桥)。

表1 非对称П型梁节段模型主要试验参数Tab.1 Main test parameters of the section model with the asymmetric П shaped girder

图4 风洞中的节段模型Fig.4 Section model in the wind tunnel

由图5可知，不同方向来流主梁的竖向涡振特性具有显著差异。从发生涡振的风攻角来看，当来流风向为0°时，主梁节段模型只有在-2.5°和-5°风攻角下发生了竖向涡振，而当来流风向为180°时，主梁在0°，±2.5°，±5°攻角下均发生了竖向涡振。对比竖向涡振最大振幅发现，来流风向为180°时的主梁竖弯涡振响应要显著大于来流风向为0°时的响应值，其中180°来流风向-5°攻角下的最大竖向涡振振幅为0.176 m，而0°来流风向-5°攻角下的最大竖向涡振振幅为0.651 m，两者相差2.7倍。对于涡振竖弯的锁定区间，两者也有显著差异，-2.5°和-5°攻角下，0°来流风向的起振风速以及竖弯锁定区间范围明显小于180°来流风向值。由图6可知，当来流方向不同时，主梁节段模型的扭转涡振特性也完全不同。0°来流风向主梁节段模型在-2.5°和-5°风攻角下发生了扭转涡振，并分别出现了两个明显的扭转涡振区，但振幅较小；当来流风向为180°时，主梁节段模型未发生扭转涡振。

(a)0°来流风向

(b)180°来流风向图5 非对称П型梁竖向涡振响应Fig.5 Vertical VIV response of the asymmetric П shaped girder

(a)0°来流风向

(b)180°来流风向图6 非对称П型梁扭转涡振响应Fig.6 Torsional VIV response of the asymmetric П shaped girder

根据以往П型梁涡振研究结果可知，该类型主梁断面的涡振主要是由于主肋与桥面板连接转角处的旋涡脱落引起的。据此，钱国伟等[16]在П型主梁的两个转角处分别安装了水平隔流板，从而打乱并削弱在该区域附近形成的旋涡，达到抑制涡振的目的。杨光辉等[20-21]通过设置封闭的中央防撞护栏并在梁底增设中央稳定板，从而将气流分离所形成的大旋涡分割成若干小旋涡，使其涡量减弱，进而抑制了涡振的发生。对于本文中的非对称П型梁，从空气动力学角度分析，在0°来流风向，由于断面在该侧存在突出的人行道板，使得来流在此处提前发生了分离，气流分离后再附点发生改变，涡激力减弱。而当来流风向为180°时，在主梁的主肋与桥面板连接转角处有较大的旋涡发生脱落，形成的涡激力相对较大，因此该来流风向的涡振较0°来流风向严重。

4 非对称主梁颤振性能

4.1 颤振临界风速

在均匀流场中对两种类型的非对称主梁进行了颤振稳定性试验，其中非对称П型梁竖向阻尼比为0.873%，扭转阻尼比为0.864%，其余参数见表1。对于非对称流线型箱梁，主要节段模型动力参数见表2。通过风速比将试验观测到的颤振临界风速换算到实桥，两种类型非对称主梁的颤振临界风速见表3，其中非对称П型梁的颤振检验风速为54.0 m/s,非对称流线型箱梁的颤振临界风速为56.0 m/s。

表2 非对称流线型箱梁节段模型动力参数Tab.2 Dynamic parameters of the section model with the asymmetric streamlined box girder

表3 非对称主梁颤振临界风速Tab.3 Flutter critical wind speeds of two types of asymmetric girders m/s

由表3可知，两种非对称主梁断面的颤振临界风速均大于相应的颤振检验风速，颤振稳定性较好。通过对比不同方向来流的颤振临界风速可以发现，0°来流风向下两种非对称主梁的颤振临界风速大于180°来流风向值，其中-3°攻角下两者颤振临界风速相差较小，随着攻角的增加，特别是在+3°攻角下，0°来流风向对应的颤振临界风速显著高于180°来流风向值。

以往试验研究结果表明[22]，水平稳定板或分离板能在一定程度上提高主梁的颤振临界风速。对于非对称П型梁，由于0°来流风向人行道板的存在，该构件在一定程度上起到了水平稳定板或分离板的作用，因此提高了该风向下的主梁颤振临界风速。对于非对称流线型箱梁，由于靠近0°来流风向的主梁上表面增设了一道人行道栏杆，这在一定程度上发挥了上稳定板的作用。根据陈政清等的研究结果可知，上稳定板可以降低扭转气动负阻尼，进而提高颤振临界风速。由此推断该人行道栏杆进一步改善了0°来流风向下主梁的颤振稳定性。

4.2 颤振导数

根据Scanlan线性自激力表达式，单位长度上受到的气动升力Lse和气动扭矩Mse分别表示为

(4)

(5)

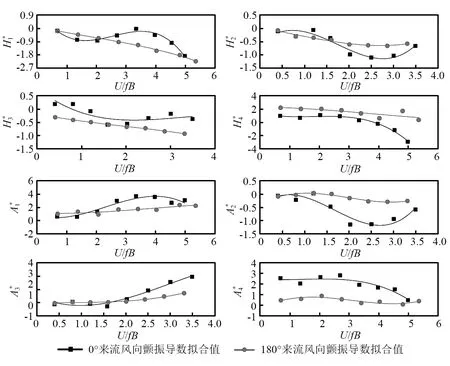
图7 非对称П型梁节段模型颤振导数Fig.7 Flutter derivatives of the asymmetric П shaped girder section model

图8 非对称流线型箱梁节段模型颤振导数Fig.8 Flutter derivatives of the asymmetric streamlined box girder section model

5 结 论

本文通过节段模型风洞试验对具有非对称人行道的П型梁和非对称流线型箱梁的气动性能进行了研究，并得出以下结论：

(1)均匀流场正攻角范围内，0°来流风向下两种类型主梁的三分力系数均大于180°来流风向值，且断面非对称性对П型梁三分力系数的影响比流线型箱梁显著。

(2)断面的非对称性会严重影响不同来流风向下主梁的涡振性能，包括出现涡振的风攻角、涡振响应振幅、起振风速以及锁定区间等。由于0°来流风向人行道板的存在，使得该方向来流提前发生了分离，气流分离后再附点发生改变，涡激力减弱，进而П型梁的涡振性能在该来流风向下得到了改善。

(4)综合以上结果，对于该种类型非对称主梁的静风荷载及其响应计算，要重点针对0°来流风向的情况。而当研究该类型非对称主梁的涡振和颤振性能时，应重点考察180°来流风向的不利情况。