地震作用下软弱夹层参数对岩质边坡锚固界面剪切作用影响

李亚鹏，言志信

(1.安徽理工大学 土木建筑学院，安徽 淮南 232001；2.河南城建学院 土木与交通工程学院，河南 平顶山 467000)

软弱夹层，因其物理力学性质差，往往是岩质边坡的薄弱部位，也是诱发边坡失稳破坏的主要原因，因此含软弱夹层岩质边坡的稳定性问题已备受岩土工程界的关注[1-3]。近年来，国内学者对动力作用下的含软弱夹层岩质边坡开展了大量的研究工作，取得了丰硕成果。范留明等[4-5]建立了软弱夹层对平面矢量波的透射模型，研究了其隔震性能和动力响应特征；刘汉香等[6]借助振动台试验设计了4种不同夹层特征的含软弱夹层斜坡，揭示了含软弱夹层斜坡的动力响应特性及变形特征；周飞等[7]开展了含软弱夹层斜坡的振动台模型试验，研究了斜坡的加速度响应特性，同时利用正交试验对影响因素进行了分析；范刚等[8]基于振动台试验和HHT(Hilbert-Huang Transform)理论，从能量角度探讨了含软弱夹层边坡的动力破坏模式。此外，另一些学者通过数值模拟对含软弱夹层岩质边坡的动力响应、变形特征及锚固参数敏感性分析等方面也进行了深入研究[9-12]。然而，目前针对地震作用下含软弱夹层岩质边坡的研究，鲜有涉及到锚杆-砂浆界面和砂浆-岩体界面两个锚固界面上的剪切作用，而该问题是边坡锚固机理研究的重点，因而值得对岩质边坡锚固界面上的剪切作用进行深入系统的研究。

鉴于此，本文利用有限差分软件FLAC3D以含软弱夹层的岩质边坡为研究对象，研究了不同软弱夹层参数对边坡位移响应和锚固界面剪切作用的影响，并结合正交试验对软弱夹层参数进行了敏感性分析。

1 计算模型建立

1.1 边坡模型

本文设计了一个含软弱夹层的岩质边坡概化模型，见图1。边坡的坡高为20 m，坡角为75°，坡顶后缘长为40 m，软弱夹层厚度D的变化范围为0.6～1.2 m，倾角β的变化范围为35°～50°，岩体重度为25 kN/m3。模型中的岩体为弹塑性材料，采用Mohr-Coulomb屈服准则，岩体物理力学参数见表1。

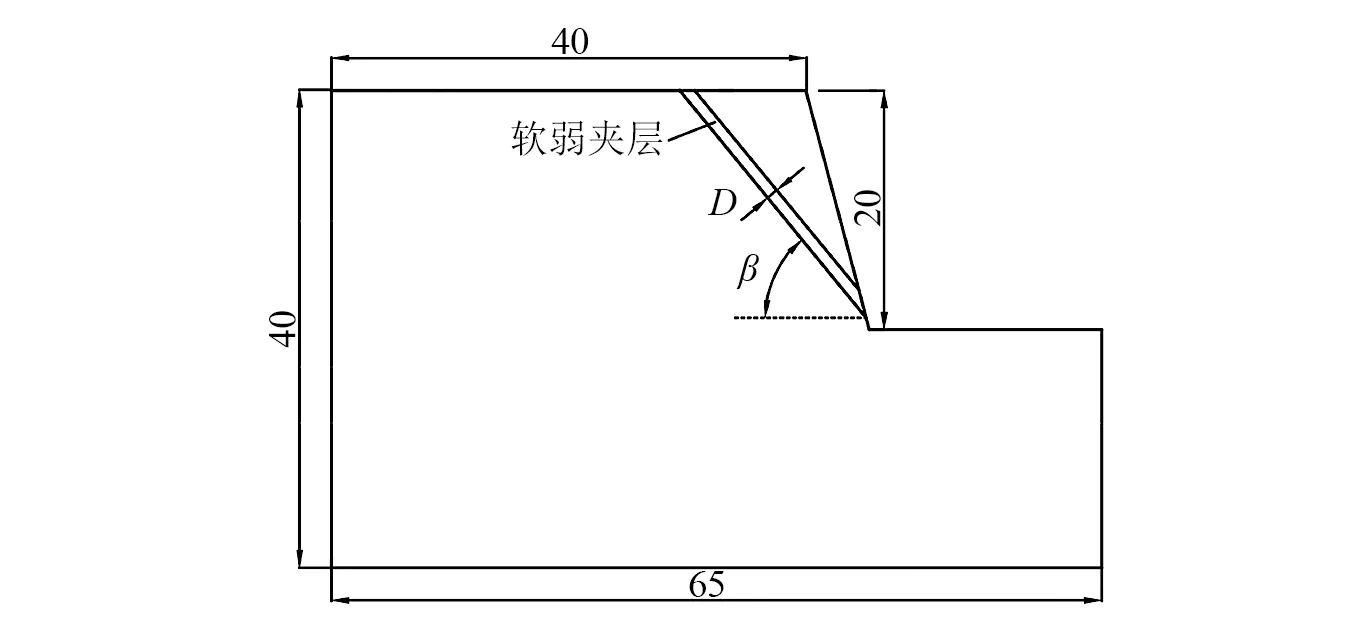
图1 岩质边坡模型(m)Fig.1 Rock slope model (m)

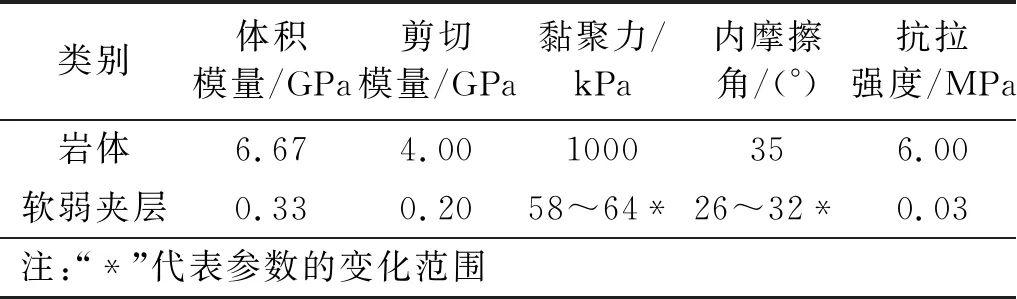
表1 岩体物理力学参数Tab.1 Physical and mechanical parameters of rock mass

1.2 支护方案

图2所示为边坡支护方案，采用全长黏结锚杆支护，自上而下共5排，依次编号为1～5#。锚杆弹性模量为210 GPa，密度为7 800 kg/m3，注浆材料强度等级为M30。锚杆倾角为15°，竖向排距为3 m，锚杆直径为30 mm，锚孔直径为120 mm，位于基岩中的锚杆锚固段长度为5 m。

图2 边坡锚杆支护设计(m)Fig.2 Design of slope with bolt (m)

1.3 锚固界面剪应力计算

本文利用FLAC3D内置的cable单元对锚固界面剪切作用进行研究。cable单元本身只能获得锚杆-砂浆界面上的剪应力，但为了获取两个锚固界面上的剪应力，首先在cable单元的建模方式上进行改进，cable单元中锚杆层和水泥浆层的参数分别采用相应锚固界面两侧材料的参数，即计算锚杆-砂浆界面剪应力时cable单元锚杆层和水泥浆层分别采用锚杆和砂浆的参数，计算砂浆-岩体界面剪应力时cable单元锚杆层和水泥浆层则分别采用复合锚固体和岩体的参数，见图3。然后分别提取cable单元各点的轴力，并代入式(1)得两个锚固界面上的剪应力。参照文献[13]和《建筑边坡工程技术规范GB 50330—2013》，本文分别取锚杆-砂浆界面和砂浆-岩体界面的极限黏结强度为8 MPa和2 MPa，当锚固界面上某点的剪应力达到极限黏结强度时，界面发生脱黏破坏。

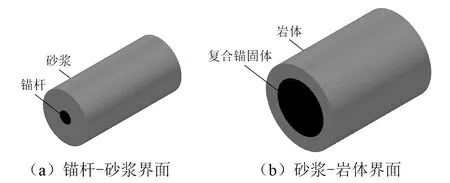
图3 计算不同界面剪应力时cable单元的建模方式Fig.3 Modeling method of cable element for calculating different interfacial shear stress

(1)

式中：τi为锚固界面上第i号和第i+1号监测点间的平均剪应力值；Pi和Pi+1分别为锚杆或锚固体上两监测点的轴力值；d为锚杆或锚固体直径；Δx为两相邻监测点的间距。

1.4 动力加载

本文选取进行了滤波和基线校正的Kobe折减波作为输入地震动，加速度峰值为2.00 m/s2，持时为10 s，施加于模型底部，加速度时程曲线见图4。模型边坡为岩质边坡，底部可认为是刚性地基，在模型四周施加自由场边界。阻尼采用局部阻尼，阻尼系数为0.158。

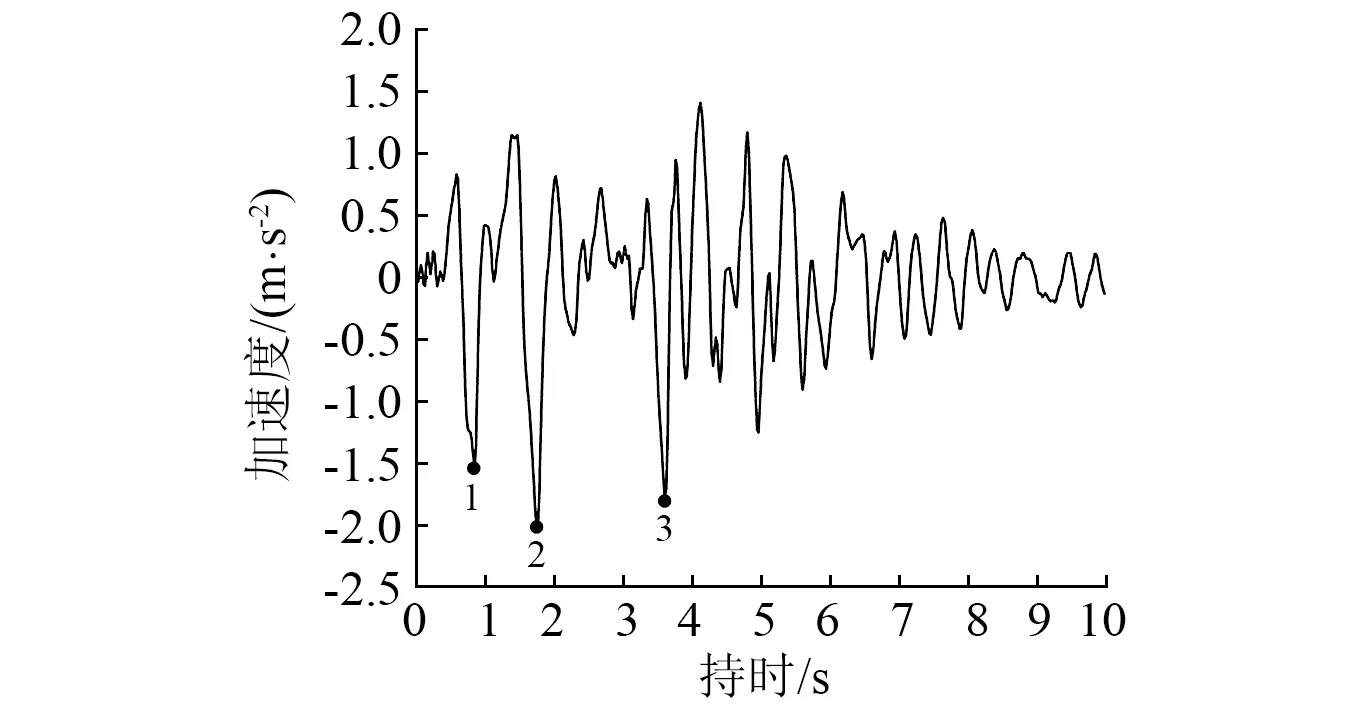
图4 计算输入的地震波加速度时程曲线Fig.4 Time-history curves of seismic wave acceleration

1.5 计算工况

为了研究软弱夹层参数对边坡位移响应及锚固界面剪切作用的影响，结合文献调研，拟定了4种工况，见表2。同时，本文分别以边坡永久位移和锚固界面上的峰值剪应力作为研究对象。

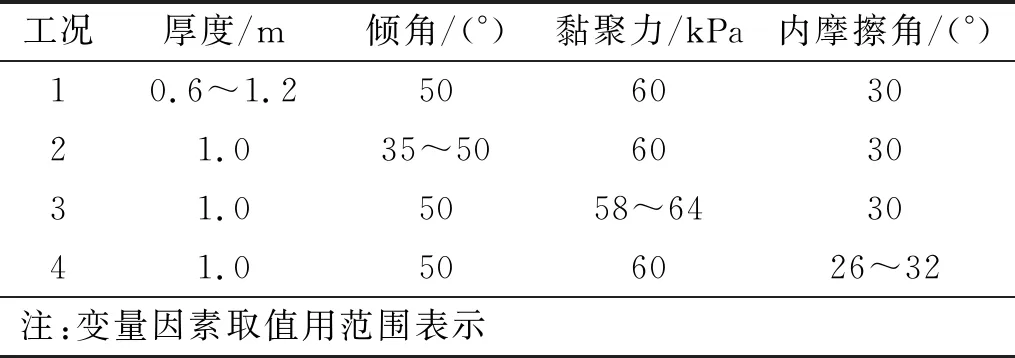
表2 不同工况下软弱夹层参数Tab.2 Weak interlayer parameters under different conditions

2 计算结果分析

2.1 锚固界面剪应力分析

由于地震作用下边坡两个锚固界面上的剪应力分布规律相似，故本文以工况1中软弱夹层厚度为0.8 m的边坡为例，对其锚杆-砂浆界面上的剪应力进行分析。此外，为了便于描述，将剪应力为零且两侧剪应力方向发生变化的点定义为中性点，将锚头至中性点这段锚杆定义为拉拔段，将中性点至锚根这段锚杆定义为锚固段。

为了研究锚固界面上的剪应力随地震动能量的变化规律，本文选取Kobe波几个主要峰值点对应的地震波输入时刻，并以3号锚杆为例，分析不同地震波输入时刻下锚杆-砂浆界面上的剪应力沿杆长的分布情况，见图5。由图5可知，不同地震波输入时刻下锚固界面上的剪应力沿杆长的分布规律相似，即界面剪应力的分布形式并未随着地震动能量变化而发生改变。界面剪应力沿杆长呈“中间大两头小”的分布形式，锚杆拉拔段和锚固段上的剪应力在软弱夹层两侧分别达到峰值，其大小接近方向相反，而后剪应力以负指数形式迅速向两端递减。这是因为危岩在地震动和重力的作用下发生变形时，位于危岩中的锚杆拉拔段受到拉拔，而危岩和基岩又通过锚杆相联系，基岩中的锚杆锚固段也会受到反向拉拔，因此锚杆与砂浆间产生相对位移，锚固界面上产生剪应力。故对于地震作用下含软弱夹层的岩质边坡，其软弱夹层两侧的锚固岩体可视为两个拉拔方向相反的动态拉拔模型。

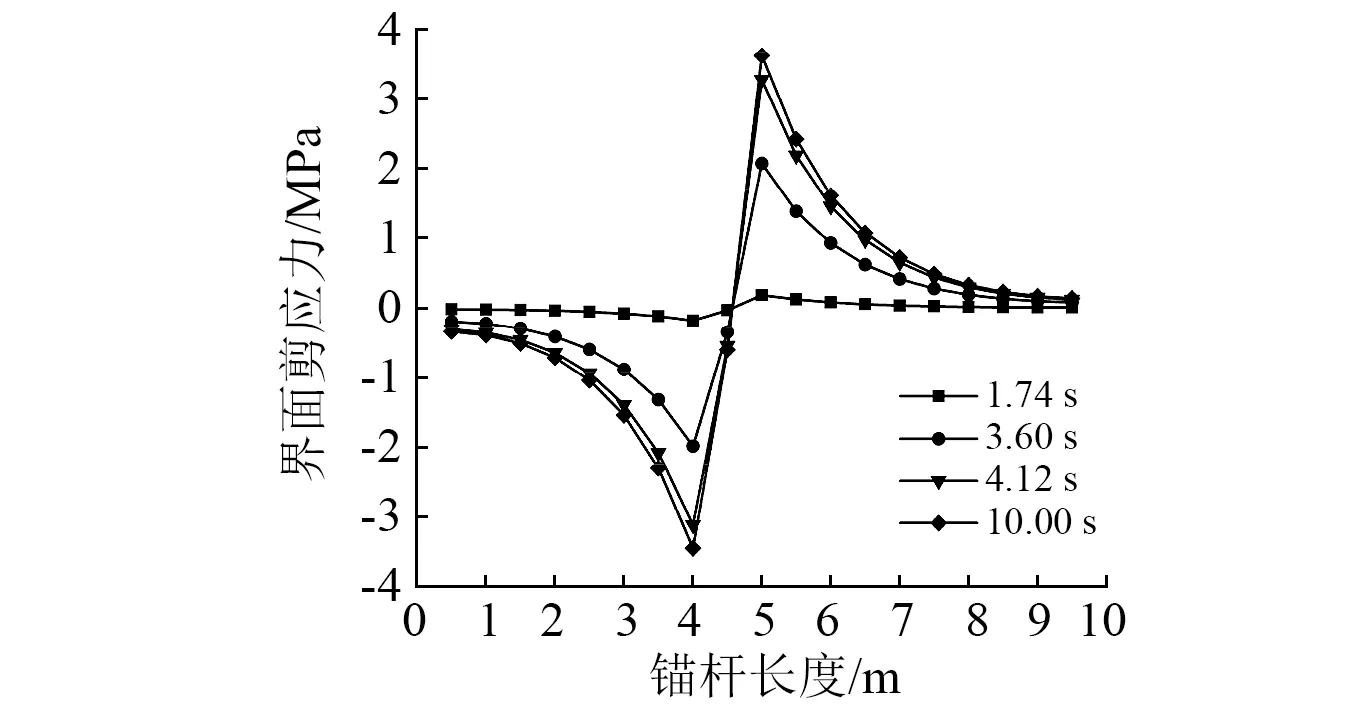
图5 3号锚杆锚杆-砂浆界面上的剪应力分布Fig.5 Bolt-grout interface shear stress distribution of No.3 bolt

图6所示为锚固界面上的峰值剪应力随时间的变化曲线。由图6可知，锚固界面上的峰值剪应力时程曲线变化规律相似。界面剪应力的变化过程可分为两个阶段，即上升阶段(0～6 s)和稳定阶段(6～10 s)，其中上升阶段中剪应力在线b,c处增幅最大。同时，结合加速度时程曲线发现，图4中点1～3对应的时间与图6中线a～c对应的时间一致。说明界面剪应力的变化与地震动能量密切相关，剪应力增大是由于较大地震动能量的激励，地震动能量减小时剪应力则基本不变，地震动能量再次增大时剪应力也会继续增大。因此上升阶段中剪应力的变化是一个动态循环过程，即随着输入地震动的激励，剪应力呈阶梯式变化，直至地震动加载后期，随着地震动能量的衰减，剪应力变化幅度逐渐减小，最后进入稳定阶段趋于恒定。

图6 峰值剪应力时程曲线Fig.6 Time history of peak shear stress distribution

2.2 软弱夹层厚度的影响

为了研究软弱夹层厚度的影响，工况1中软弱夹层厚度分别取0.6 m,0.8 m,1.0 m,1.2 m，模拟结果见图7和图8。

由图7和图8可知，随着软弱夹层厚度的增加，边坡永久位移逐渐增大，由17.67 mm增至37.67 mm，增大了1.13倍；锚固界面上的峰值剪应力随着厚度的增加也逐渐增大。这是因为软弱夹层厚度的增加，危岩更易发生变形破坏，锚固系统则需要提供更大的锚固力以遏制边坡的变形。说明永久位移和峰值剪应力二者的变化密切相关，且变化规律大体相同。

2.3 软弱夹层倾角的影响

为了研究软弱夹层倾角的影响，工况2中软弱夹层倾角分别取35°,40°,45°,50°，模拟结果见图9和图10。

由图9和10可知，随着软弱夹层倾角的增大，边坡永久位移和锚固界面上的峰值剪应力并非呈单一的增大或减小，而是呈现先增大(倾角小于45°)后减小(倾角大于45°)的分布规律。其中倾角在35°～45°时，随着倾角的增大，永久位移和峰值剪应力的增速由快变慢。说明软弱夹层倾角较大或较小时，边坡稳定性较好；而倾角为45°左右时，对边坡的稳定性最不利。

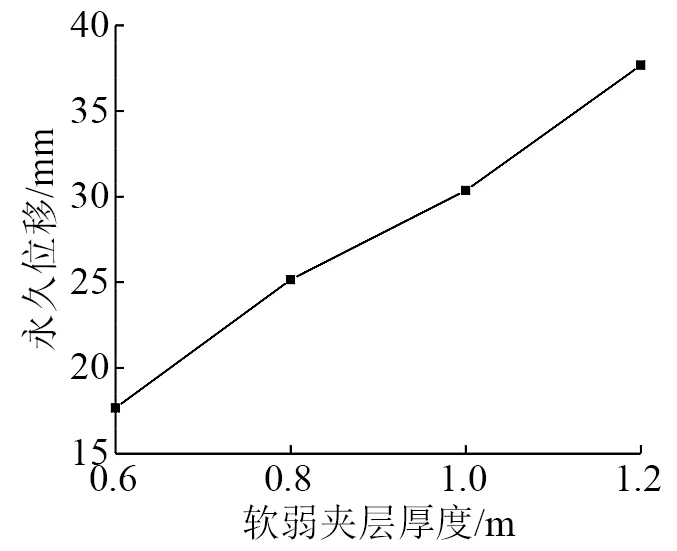
图7 软弱夹层厚度与边坡永久位移的关系Fig.7 Relationship between weak interlayer thickness and permanent displacement of slope

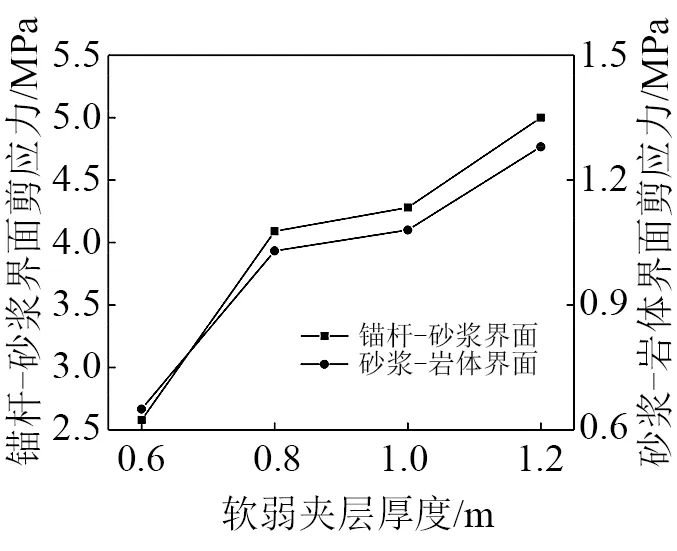
图8 软弱夹层厚度与峰值剪应力的关系Fig.8 Relationship between weak interlayer thickness and peak shear stress

图9 软弱夹层倾角与边坡永久位移的关系Fig.9 Relationship between weak interlayer dip and permanent displacement of slope

图10 软弱夹层倾角与峰值剪应力的关系Fig.10 Relationship between weak interlayer dip and peak shear stress

2.4 软弱夹层黏聚力的影响

为了研究软弱夹层黏聚力的影响，工况3中软弱夹层黏聚力分别取58 kPa,60 kPa,62 kPa,64 kPa，模拟结果见图11和图12。

由图11和图12可知，随着软弱夹层黏聚力由58 kPa增至64 kPa，边坡永久位移减幅达77%，锚固界面剪切作用也减弱，峰值剪应力减幅达74%。说明增大软弱夹层黏聚力，亦即增大其抗剪强度，可明显提高边坡的稳定性，对边坡永久位移和锚固界面上的剪应力有重要影响。

2.5 软弱夹层内摩擦角的影响

为了研究软弱夹层内摩擦角的影响，工况4中软弱夹层内摩擦角分别取26°，28°，30°，32°，模拟结果见图13和图14。

由图13和图14可知，随着软弱夹层内摩擦角由26°增至32°，即抗剪强度增大，边坡永久位移和锚固界面上的峰值剪应力均逐渐减小，减幅约46%。说明软弱夹层内摩擦角的改变，对边坡永久位移和锚固界面上的剪应力影响显著。

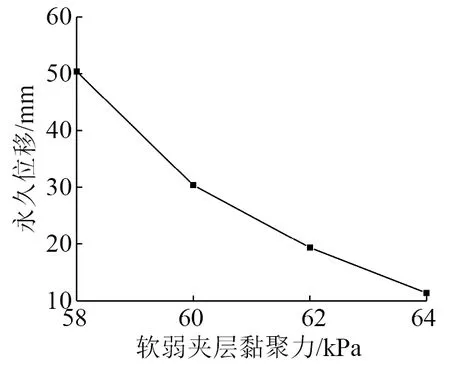
图11 软弱夹层黏聚力与边坡永久位移的关系Fig.11 Relationship between weak interlayer cohesion and permanent displacement of slope

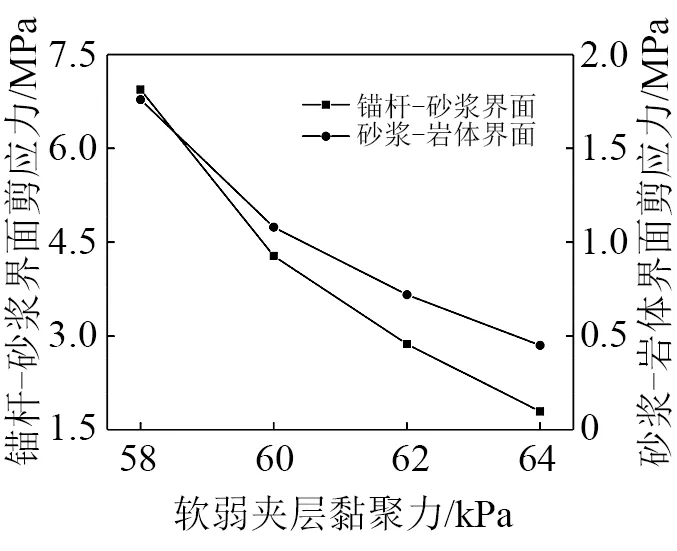
图12 软弱夹层黏聚力与峰值剪应力的关系Fig.12 Relationship between weak interlayer cohesion and peak shear stress

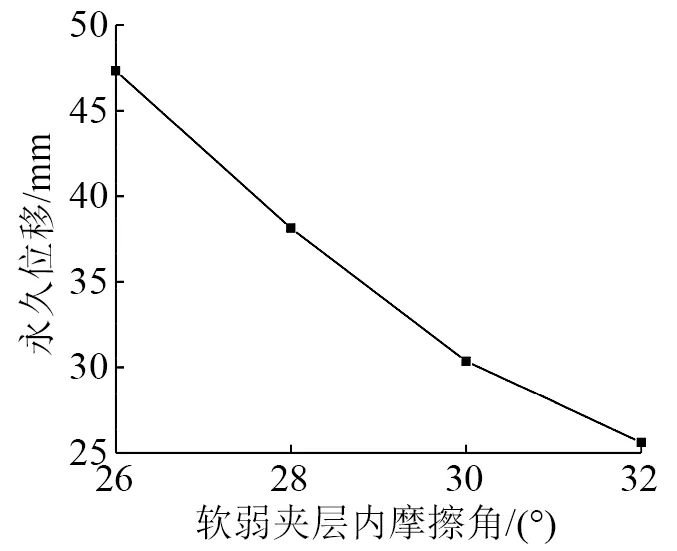
图13 软弱夹层内摩擦角与边坡永久位移的关系Fig.13 Relationship between weak interlayer internal friction angle and permanent displacement of slope

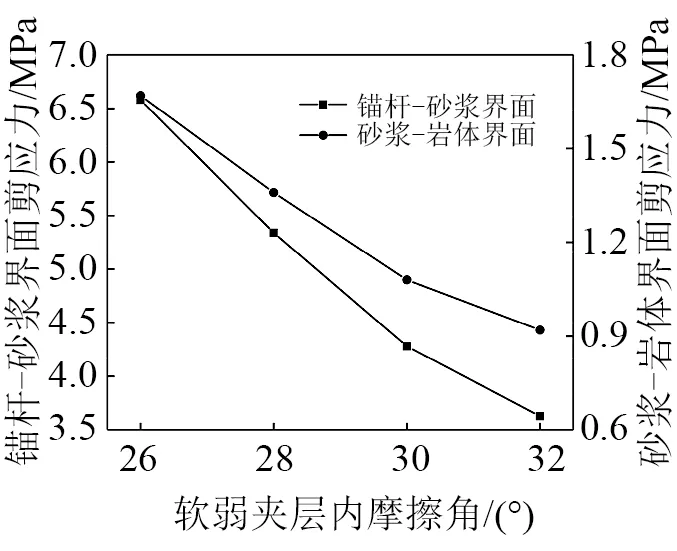
图14 软弱夹层内摩擦角与峰值剪应力的关系Fig.14 Relationship between weak interlayer interna friction angle and peak shear stress

3 软弱夹层参数敏感性分析

前文研究了各软弱夹层参数对边坡永久位移和锚固界面上剪应力的影响，但存在一定的局限性。为了进一步研究软弱夹层多个参数对边坡锚固界面上剪应力的影响，本文采用多因素分析中最常用的正交试验设计法，对多个软弱夹层因素的敏感性进行分析。正交试验考虑前文中的4个影响因素，每个影响因素有3个水平。同时，为了避免人为因素导致的系统误差，对因素水平并非按数值大小依次排列，而是进行了“随机化”处理[14]，见表3。

表3 影响因素水平表Tab.3 Influence factors level table

基于正交试验原理，假设各影响因素间无交互作用，对所确定的4个影响因素选用L9(34)正交表安排试验，再计算各试验方案下锚固界面上的峰值剪应力，由此研究各影响因素对锚固界面剪切作用的敏感性。正交试验方案及计算结果见表4。

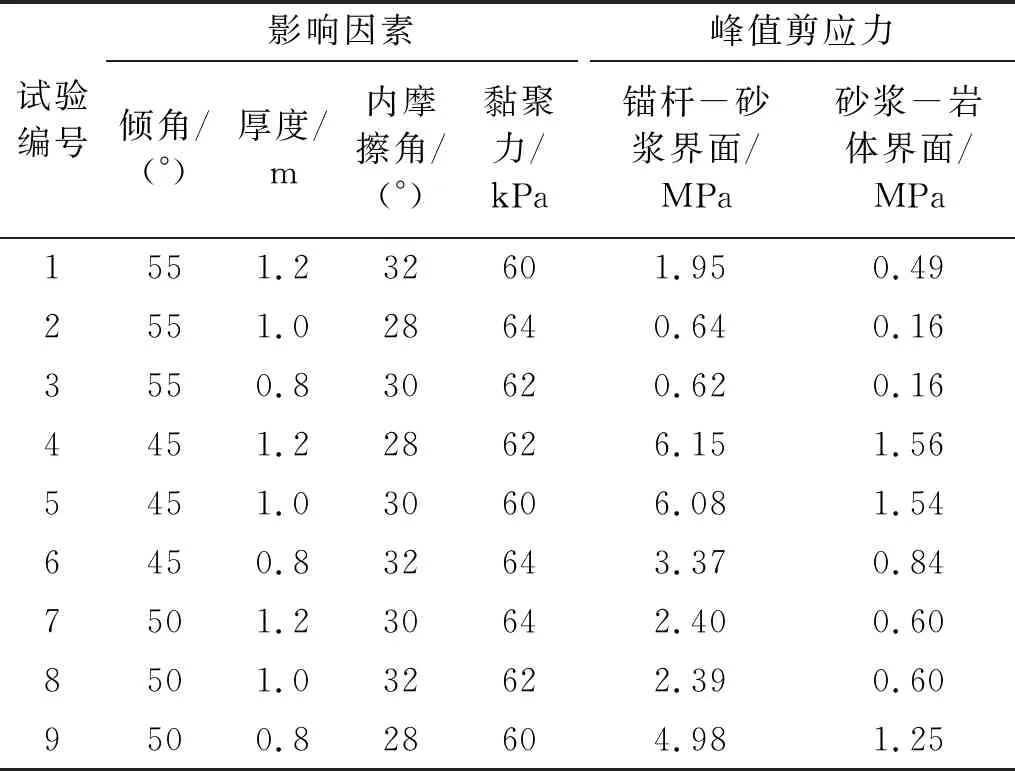
表4 试验方案及计算结果Tab.4 Scheme and results of orthogonal experiment

3.1 极差分析法

对于正交试验结果的分析，常有极差分析法和方差分析法两种。其中极差分析法，简单易懂，实用性强，以极差Rj作为评价影响因素对试验结果影响程度的指标，计算公式为

Rj=max{k1,j,k2,j,…,kij}-min{k1,j,k2,j,…,kij}

(2)

式中：kij为第j因素i水平对应计算结果的平均值。

极差越大说明对试验结果影响越大，对试验结果越敏感。本文采用极差分析法对表4计算结果进行处理，结果见表5和表6。

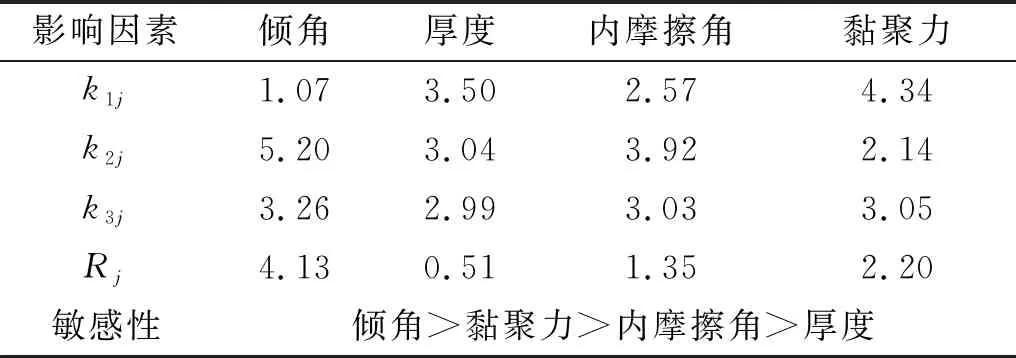
表5 极差分析表(锚杆-砂浆界面)Tab.5 Range analysis table(bolt-grout interface)

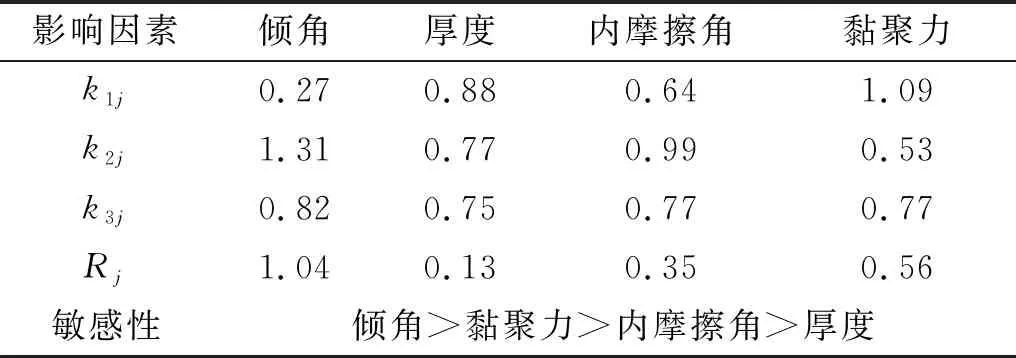
表6 极差分析表(砂浆-岩体界面)Tab.6 Range analysis table(grout-rock interface)

由表5和表6可知，软弱夹层参数对锚固界面剪应力的敏感性由大到小依次为：软弱夹层倾角、黏聚力、内摩擦角和厚度。

3.2 层次分析法

为了进一步获得因素各水平对锚固界面上剪应力的影响权重，即对界面剪应力的影响大小，采用层次分析法(Analytic Hierarchy Process，AHP)[15]对正交试验结果做进一步处理。

影响权重ω为

ω=ASCT

(3)

水平层对试验结果的影响效应矩阵A为

(4)

式中：若试验指标越大越好，则Mij=kij；反之，Mij=1/kij。

(5)

矩阵AS称为水平标准影响效应矩阵。

因素对试验结果的影响权重矩阵C为

(6)

式中：Rj为极差分析法中的极差。

由于界面剪应力和边坡永久位移二者的变化规律密切相关。界面剪应力越大，边坡的永久位移也越大，边坡稳定性则越差。因此在计算水平层对试验结果的影响效应矩阵A时，认为试验指标越大越不好，令Mij=1/kij，结果见表7。

由表7可知，因素各水平对两个锚固界面上剪应力的影响权重相同。软弱夹层倾角的3个水平中，A1的影响权重最大；软弱夹层厚度的3个水平中，B3的影响权重最大；软弱夹层内摩擦角的3个水平中，C1的影响权重最大；软弱夹层黏聚力的3个水平中，D2的影响权重最大。各因素的主次顺序由因素各水平的影响权重之和决定，可得主次顺序依次为：软弱夹层倾角、黏聚力、内摩擦角和厚度。这与极差分析法得到的结论一致。

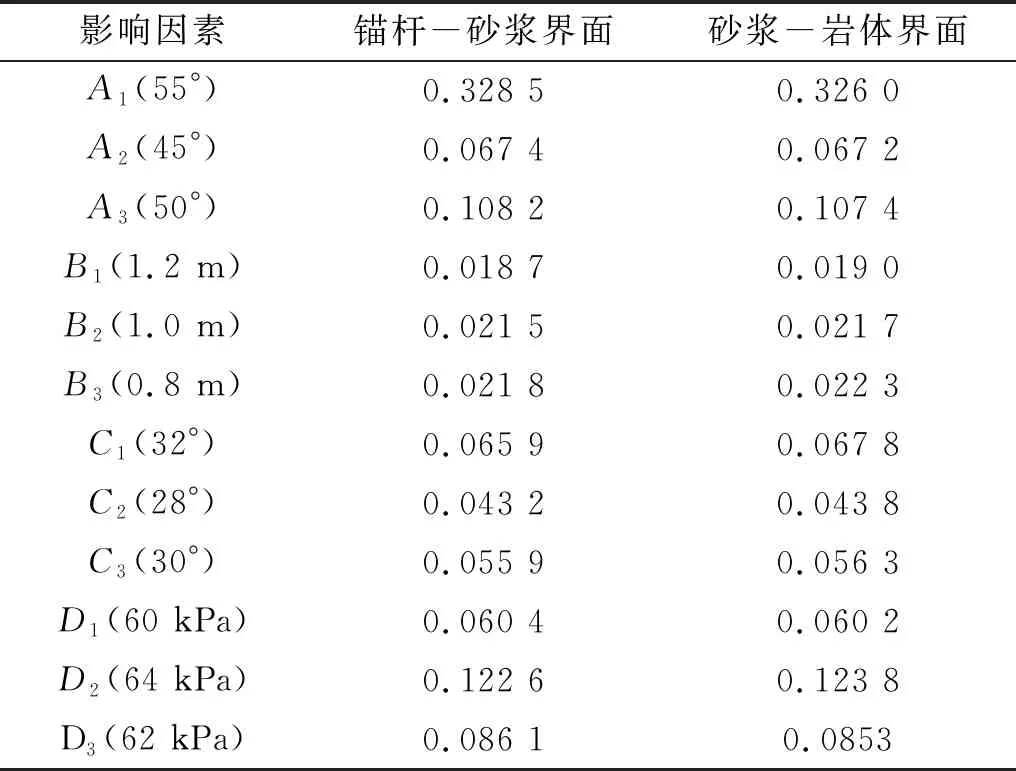
表7 因素各水平对界面剪应力的影响权重Tab.7 Impact weight of each level of factor on interface shear stress

4 结 论

通过一个含软弱夹层锚固岩质边坡的数值模拟算例，研究了锚固界面上的剪应力在地震作用下的分布规律，分析了不同软弱夹层参数与边坡位移响应和锚固界面剪切作用的关系，并结合正交试验进行了软弱夹层参数的敏感性分析。结论如下:

(1)锚固界面上的剪应力呈“中间大两头小”的分布形式，剪应力在软弱夹层两侧达到正负峰值，以负指数形式迅速向锚杆两端递减。地震作用下含软弱夹层的岩质边坡，其软弱夹层两侧的锚固岩体可看作两个拉拔方向相反的动态拉拔模型。

(2)界面剪应力的变化与地震动能量密不可分，其变化过程可分为上升阶段和稳定阶段两个阶段，其中在上升阶段中界面剪应力的变化是一个动态循环过程，界面剪应力随着输入地震动的激励呈阶梯式变化。

(3)不同软弱夹层参数对边坡位移响应和锚固界面上的剪切作用影响不同，且坡体永久位移和锚固界面上的峰值剪应力有着内在的联系，二者的变化规律大体相同。

(4)基于多因素正交试验，分别利用极差分析法和层次分析法对软弱夹层参数的敏感性进行分析，得出一致的结论。4个影响因素对锚固界面剪切作用的敏感性具有明显差异，其中软弱夹层倾角对界面剪应力最敏感，厚度对界面剪应力最不敏感。