整车驻车制动时载荷及制动距离分析

王伟

(上海汽车变速器有限公司，上海 201807)

0 引言

驻车系统是自动变速器和新能源减速器中的一种安全装置，其作用是将变速器输出轴锁止在变速器壳体，以确保整车安全制动[1-2]。目前国内对驻车系统制动载荷及制动距离研究较少，文献[3]中虽然分析了驻车系统动态载荷，但未考虑制动加速度影响，也没有分析动态载荷与驻车锁止车速的影响。我国制动系统强制性标准GB 7258-2017《机动车运行安全技术条件》[4]规定了行车制动距离的要求，但未对坡度驻车制动距离进行规定。针对以上情况，结合驻车制动运动状态，引入整车静态振荡临界速度、“拒绝溜坡”车速，优化数学模型。并推导出动态载荷、制动距离和驻车锁止车速等关系，为后续驻车系统开发提供一定指导。

1 静态载荷分析

驻车系统静态载荷是指汽车停止在坡道上驻车齿轮需承受的最大扭矩。

图1为车辆停在坡度上的受力情况，车辆在坡道时受到静态载荷——地面摩擦力Ff和重力分力的作用保持相对静止。

图1 车辆静态载荷分析

整车受到的静态载荷——地面摩擦力Ff：

Ff=mgsinα1

(1)

驻车齿轮受到静态载荷——最大静态扭矩Tt：

(2)

式中：m为汽车总质量(kg)；α1为静态最大坡道倾角(°)；R1为汽车车轮静态半径(m)；i为驻车齿轮至半轴传动比。

2 动态载荷分析

驻车系统动态载荷是指汽车以安全速度锁止时，驻车齿轮所受到的冲击载荷。按照整车工况可分为平路前行工况、平路倒车工况、坡道上坡工况、坡道下坡工况。

2.1 平路前行工况

图2为平路前行工况的整车受力分析情况。

图2 平路前行工况整车受力分析

整车受到动态载荷——地面摩擦力Ff：

Ff=ma

(3)

由上式可得：

(4)

在平路前行工况下，驻车齿轮受到动态载荷Tsf1：

(5)

式中：a为驻车制动加速度(m/s2)；μ为驻车制动摩擦因数；l为整车轴距(m)；lv为汽车总质量下质心至驱动轴距离(m)；h为汽车总质量下质心高度(m)；Nf为汽车驱动轴受到正压力(N)；Nh为汽车非驱动轴受到正压力(N)；R2为汽车车轮滚动半径(m)。

由公式(3)也可计算出制动摩擦因数

(6)

当整车以一安全速度驻车制动时，车辆会出现两种制动状态：(1)整车滑行+静态振荡制动；(2)静态振荡制动。当处于整车滑行阶段，制动摩擦因数μ=车辆滑行摩擦因数μslip；当处于这两种状态的静态振荡时，制动摩擦因数μ与整车制动频率f有关，且小于滑行摩擦因数μslip。

当整车静态振荡制动时，可将整车运动简化为图3所示简谐振动。

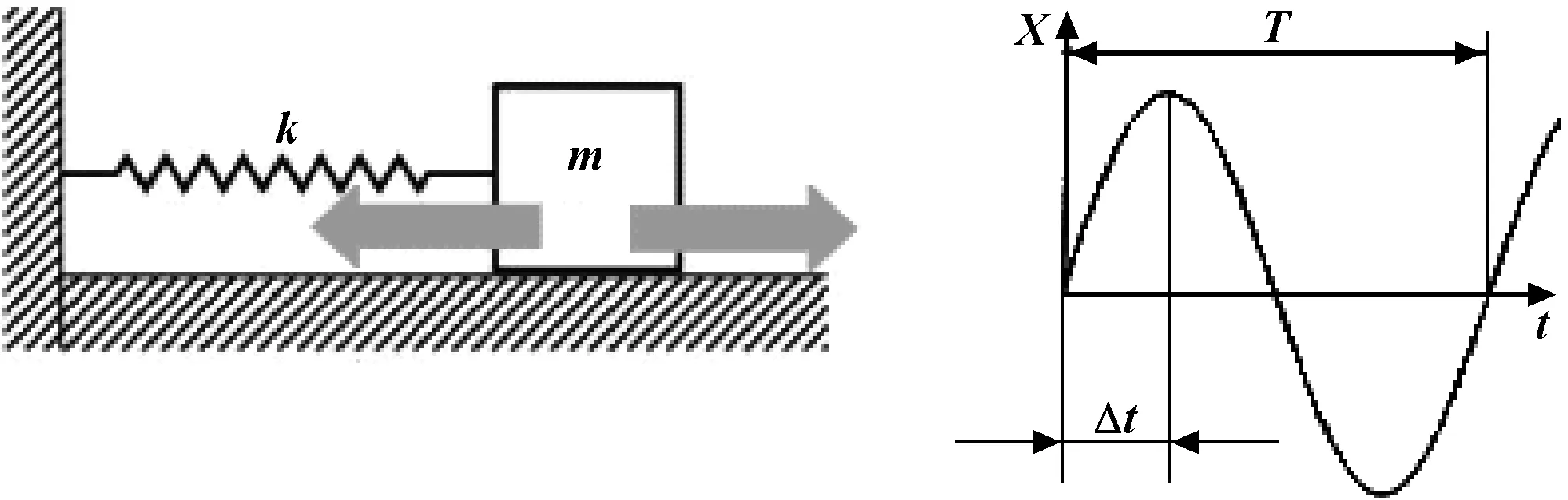
图3 整车静态振荡可简化为一简谐振动

静态振荡时位移Xv：

(7)

静态振荡时弹簧刚度K：

K=m(2πf)2

(8)

静态振荡时地面最大摩擦力Ff：

Ff=KXvmax=2πfvvm

(9)

静态振荡时，驻车齿轮受到动态载荷Tsf1：

(10)

式中：vv为整车振荡制动时初始速度(m/s)；f为整车制动频率(Hz)；t为整车振荡时间(s)。

由式(6)—式(8)可计算出整车由滑行运动向静态振荡运动转变时临界速度vs：

(11)

驻车制动摩擦因数μ可表示为

(12)

则平路前行工况的驻车系统动态载荷Tsf1也可表示为

(13)

式中：vp为驻车锁止车速(m/s)。

2.2 平路倒车工况

图4是平路倒车工况的整车受力分析情况，则驻车齿轮受到动态载荷Tsf2：

(14)

整车由滑行运动向静态振荡运动转变时临界速度vs：

(15)

则平路倒车工况的驻车系统动态载荷Tsf2也可表示为

(16)

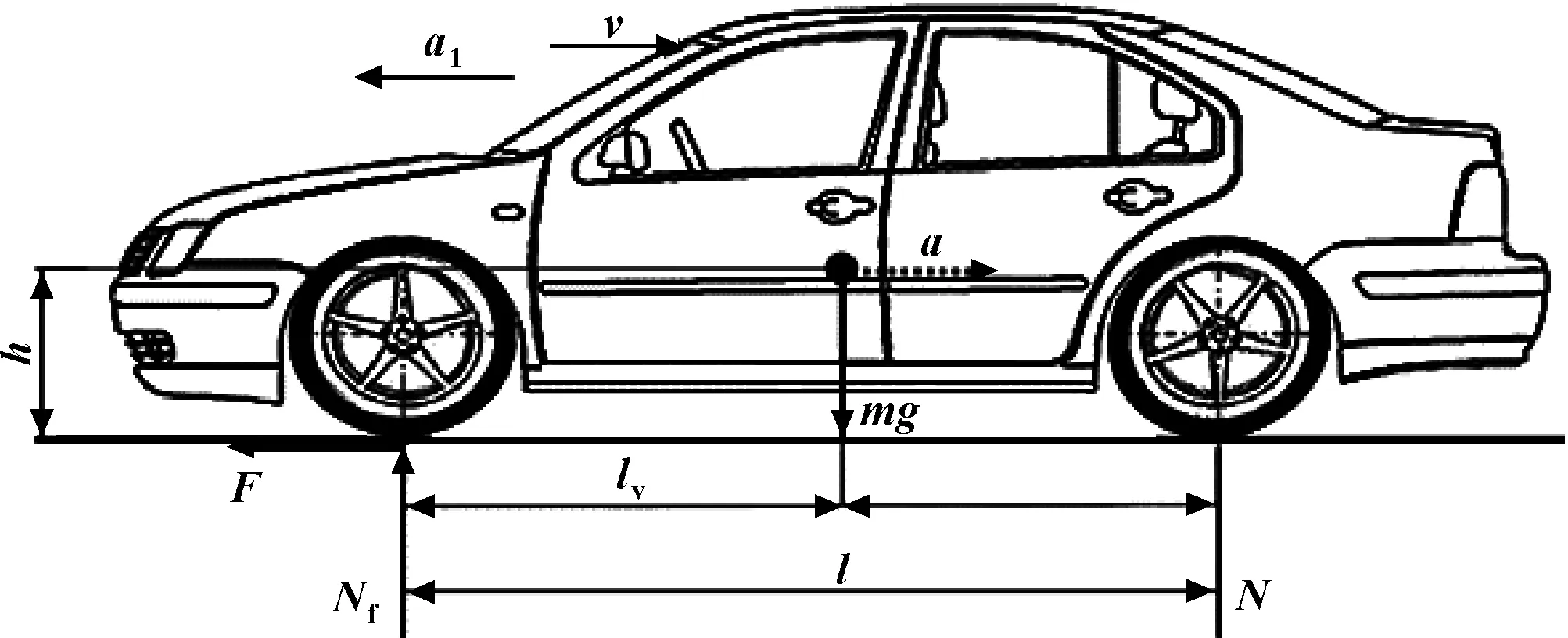
图4 平路倒车工况整车受力分析

2.3 坡道下坡工况

图5是坡度下坡工况的整车受力分析情况，则驻车齿轮受到动态载荷Tsf3：

(17)

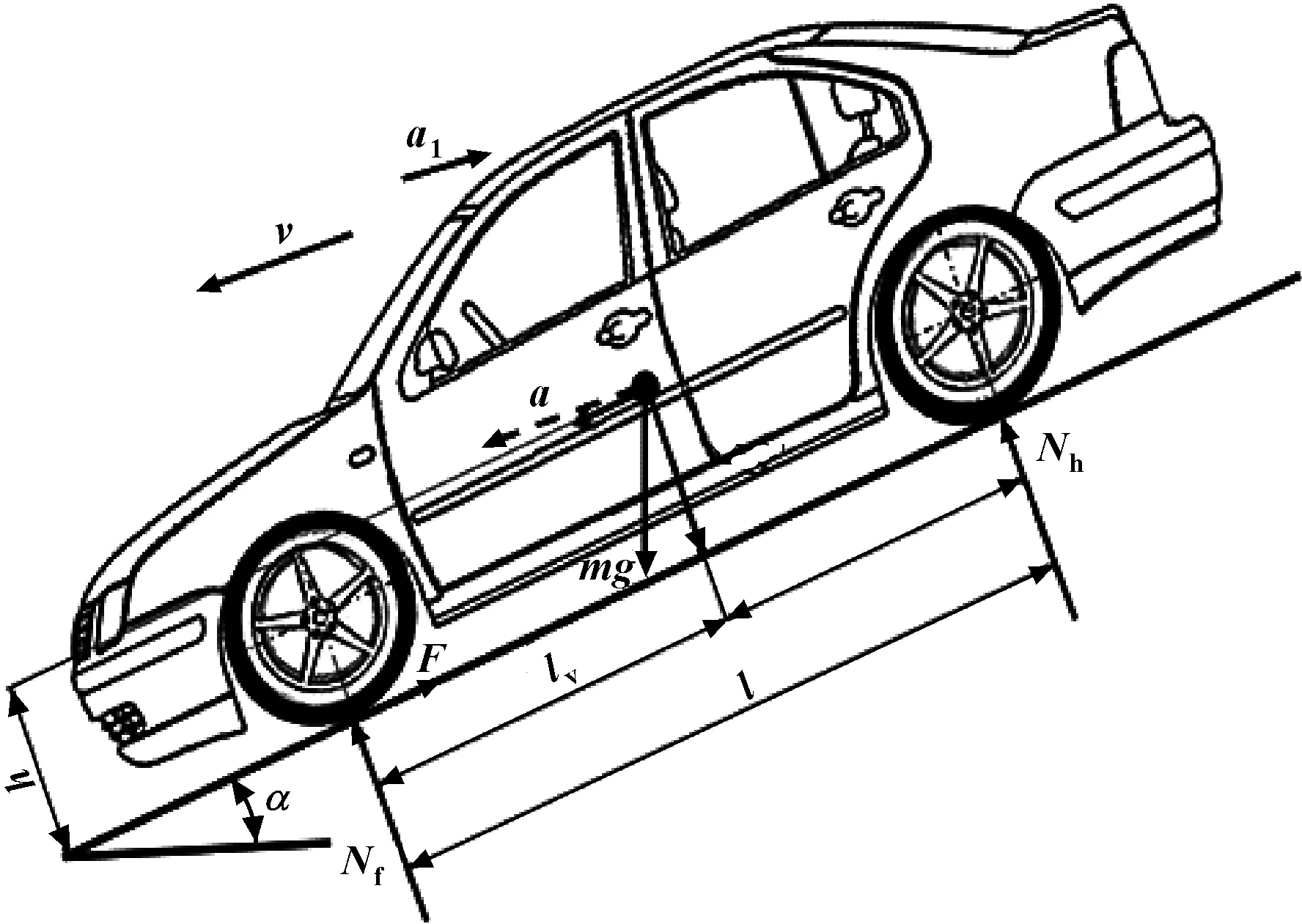
图5 坡度下坡工况整车受力分析

同样，若整车在坡道上驻车振荡制动时，其振荡距离与振荡刚度计算公式与平路工况一致。

整车由滑行运动向静态振荡运动转变时临界速度vs：

(18)

则坡度下坡工况的驻车系统动态载荷Tsf3也可表示为

(19)

式中：α为动态最大坡道倾角(°)。

2.4 坡道上坡工况

图6是坡度上坡工况的整车受力分析情况，则驻车齿轮受到动态载荷Tsf4：

(20)

图6 坡道上坡工况整车受力分析

整车由滑行运动向静态振荡运动转变时临界速度vs：

(21)

则平路倒车工况的驻车系统动态载荷Tsf4也可表示为

(22)

3 坡道制动距离计算

当车辆挂入P挡停在最大坡度上，由于存在不利的“齿对齿”位置，棘爪和驻车齿轮齿顶接触，在坡道方向分力作用下，棘爪必须安全地啮入到下一个齿中，到齿轮下一个齿的旋转角度必须被设计或满足由车辆自身引起的瞬时驱动速度不会导致“拒绝需求”，若驻车锁止车速vp小于此驱动速度vd时，可能会发生车辆在坡度溜坡现象，致使车辆无法入P挡。因此要求驱动速度vd需不大于驻车锁止车速vp，此驱动速度vd即为“拒绝溜坡”车速或最小驻车锁止车速。

当整车在坡道上静态驻车制动时，若“拒绝溜坡”车速vd>vs时，整车运动状态分三个阶段：第一阶段，棘爪啮入驻车齿轮齿槽前，由于存在不利的“齿对齿”位置，整车滚动向前运动，此阶段整车移动距离为滚动行驶距离sro；第二阶段，棘爪啮入驻车齿轮齿槽中，整车滑行前行，此阶段整车移动距离为滑行行驶距离sslip；第三阶段，整车车轮停止运动，但整车车身会处于图3所示静态振荡运动，此阶段车身振荡位移如公式(7)所示。若“拒绝溜坡”车速vd≤vs时，整车运动仅有第一和第三阶段，无第二阶段滑行制动。

当vd>vs时，整车在第二、三阶段运动满足动能守恒定律：

(23)

由公式(7)(9)(23)可求得整车滑行距离：

(24)

由上述所知，若只考虑车轮制动距离s1：

(25)

另一方面，当整车驻车制动时，若需评估整车与前车安全距离s，则需要考虑第三阶段——整车静态振荡。

(26)

4 案例分析

某新能源整车总质量m=4 325 kg，轴距l=4 150 mm，质心距驱动轴距离lv=2 338 mm，质心高度h=760 mm，轮胎滑行摩擦因数μslip=0.85，制动频率f=1.4 Hz，轮胎半径R=354 mm，静态最大坡度为25%，动态最大坡度为11.6%，驻车系统至半轴速度i=9.99，计算此驻车系统静动态载荷和临界速度，并分析当驻车齿轮齿数z=6、7、8、9、10、11、12时，整车车轮最大制动距离s1和整车需求得最大安全距离s。

表1为动态工况的临界速度，图7为驻车系统载荷与锁止车速关系。

由表1和图7可得：

(1)当驻车锁止车速vp≥vs时，整车制动会出现先滑行再静态振荡制动，在4种工况中，最大动态冲击载荷出现在平路前行工况，最小动态冲击载荷出现在坡度上坡工况。

(2)当驻车锁止车速vp

(3)在4种工况下，坡度上坡临界速度vs最小，平路前行临界速度vs最大。

图8为驻车齿轮齿数与驻车制动距离的关系。

图8 驻车齿轮齿数与驻车制动距离的关系

由图8可得：

(1)驻车齿轮齿数z越大时，整车车轮最大制动距离和整车需求最大安全距离越小；

(2)坡道上坡制动距离大于坡道下坡制动距离，主要是由于坡道上坡临界速度vs小于坡道下坡临界速度，导致其滑行距离较大。

5 结束语

(1)当整车以一安全速度驻车制动时，整车会存在两种制动状态：滑行+静态振荡及静态振荡，据此引入临界速度vs(滑行运动向静态振荡运动转变时的速度)，分析了动态载荷、驻车锁止车速vp、临界速度vs之间关系。

(2)当整车挂入P挡在坡道上静态驻车时，根据“拒绝溜坡”车速vd与临界速度vs关系，整车存在两种运动状态：若vd>vs时，整车先滚动，再滑行，最后是静态振荡；若vd≤vs时，整车滚动+静态振荡。文中分析了制动距离、“拒绝溜坡”车速、临界速度之间的关系。并得出随着齿数越大，“拒绝溜坡”车速越小，制动距离及安全距离越小。