麦弗逊前悬架硬点布置分析

韦仲宁，林明，杨魏绮

(广西艾盛创制科技有限公司，广西柳州 545006)

0 引言

在汽车设计中，因麦弗逊悬架体积比较小，有利于紧凑的发动机舱布置。其中，麦弗逊式悬架的主要结构是由螺旋弹簧加上减振器以及A字下摆臂组成。麦弗逊悬架应用广泛，微型车、紧凑车、中级车以及SUV车型上都能见到麦弗逊悬架的身影。因而，未来汽车将采用整体模块化的研发设计思路。

其中，底盘平台的正向布置与模块化架构，将涉及到底盘基本参数的选择与确定：底盘悬架总成、子系统甚至零部件的模块化架构策略，底盘系统硬点的正向布置，底盘运动校核等方面内容。本文作者将以麦弗逊悬架的正向设计探讨底盘平台模块化架构及相关问题。

1 基准的确定

1.1 坐标确定

根据整车坐标系定义及前轮距Df，分别得到左前轮中心点TL坐标(0，-Df/2，0)、右前轮中心点TR坐标(0，Df/2，0)。根据车轮(轮胎、轮辋)、车轮偏距ET、制动盘厚度及驱动半轴等，大致确定摆臂外球销点G的YZ坐标，见图1。要求摆臂球销到驱动轴间隙s1在8 mm以上，制动盘到摆臂间隙s2在12 mm以上(如有制动防尘板，则制动器与防尘板之间间隙要求大于6 mm，防尘板与摆臂间隙要求大于7 mm)。在空间允许范围内，尽可能地将摆臂球销往外布置。

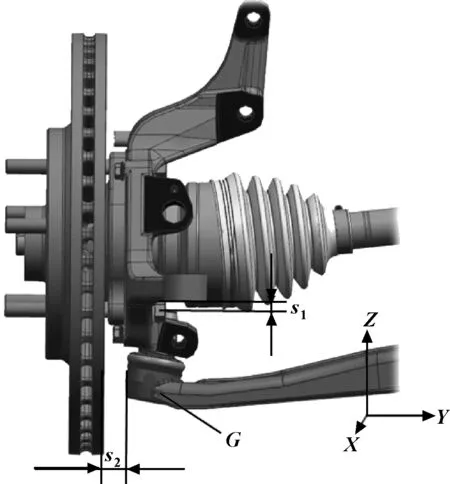
图1 左摆臂外点间隙

1.2 主销布置

1.2.1 主销内倾角

如图2(a)所示，在过车轮中心点TL的YZ平面上，作线段TLB(长度等于车轮静半径)，TLB与Z轴夹角为车轮外倾角(参考值-1°～1°)，点B即为车轮接地点，TLB为车轮中心平面与YZ平面交线。过点B作平行于Y轴线段BC，长度为在地面上的主销偏移距(参考值-18～+30 mm)，点C即为主销与地面交点在YZ平面的投影点。连接CG，CG与Z轴夹角即为主销内倾角(11°～15°)。轮心处的主销偏移距rw(参考值50～60 mm)，最大值不能超过75 mm。

1.2.2 主销后倾角

如图2(b)所示，在过车轮中心点TL的XZ平面上，做竖直向下线段BTL，BTL长度等于车轮静半径。以B为起点作平行于X轴直线BC，即为在地面上的主销后倾角偏距(参考值11～25 mm)，点A即为主销与地面交点在XZ平面的投影点。连接ATL，ATL与Z轴的夹角即为主销后倾角(参考值2°～6°)。主销后倾角应该考虑地面线的影响(轮心处的主销后倾角偏距很小，甚至为0)，ADAMS里面却没有考虑地面线。

图2 主销内倾角、主销后倾角

1.2.3 摆臂球销点G、减振器硬点确定

过GC做过X轴的拉伸平面、过GA做过Y轴的拉伸平面，两平面的交线L即为主销轴线。此时可以在直线L上选择摆臂外球销点G的位置，从而确定点G的坐标。减振器上点(Top_mount，简称点T)就落在主销轴轴线上，根据定义的轮心到减振器上点在Z轴方向距离，确定减振器上点位置(考虑空载时弹簧长度、满载时弹簧下座与轮胎间隙，该间隙要求在15 mm以上)。减振器在车辆的横向平面(YZ面)是倾斜的(主销内倾)，这对侧倾中心有影响，在减振器与轮胎的间隙要求15 mm以上时，将减振器尽量靠近车轮。减振器在车辆的纵向平面存在一定的倾角(主销后倾角)，这个倾角对车辆纵倾中心有影响，可以限制转向轴(倾角)在一定的位置上。在布置麦弗逊悬架时，在侧视图上要求减振器轴线、弹簧轴线与主销轴线重合，主销轴线尽可能靠近轮心点，如图3所示。

图3 减振器轴线、弹簧轴线与主销轴线侧视图

根据减振器与轮心的位移传动比i、减振器储油筒大小、减振器与轮胎间隙要求、驱动半轴包络，确定减振器下点位置。图4所示为麦弗逊悬架减振器传动比简图。

图4 减振器杠杆比

i=L/(Wcosσ)

(1)

式中：σ为减振器轴线与主销轴线夹角；W为减振器下安装点到极心的距离；L为轮心在地面垂直投影到极心的距离。

对于减振器传动比i的取值范围一般为0.85～0.98，精确值可以用ADAMS软件计算仿真得到。

1.3 整车中心

1.3.1 侧倾中心

根据侧倾中心高度确定等效摆臂内点D。侧倾中心是指通过车轮中心的横向垂直平面上的一点，在这点上给车身施加一个侧向力，可以不产生侧倾角运动。麦弗逊式悬架的侧倾中心可通过图解法获得(见图5)。在布置时，通过侧倾中心高度反推出等效摆臂内点，再根据纵倾中心确定摆臂前、后内点位置。

图5 麦弗逊悬架侧倾中心的确定

麦弗逊悬架的侧倾中心如图5所示，利用作图法得出：从悬架与车身的固定连接点T作减振器轴线TG的垂直线TP，并将等效摆臂线GD延长，两条直线的交点即为极心P。将点P与车轮接地点N连线，与左右中轴线的交点W，即为侧倾中心。

在布置时，已知减振器上点T、摆臂外点G，由图5可知摆臂前、后内点连线上的摆臂等效内点D落在直线GP上，则麦弗逊悬架侧倾中心的高度hw为

(2)

等效摆臂的长度受大梁、副车架等位置的限制。具体设计摆臂时，在满足布置要求的前提下，应尽可能加长摆臂长度。摆臂越长，轮距Df变化越平缓，即车轮跳动时轮距变化越小，越有利于提高轮胎寿命。同时主销内倾角、车轮外倾角和主销后倾角等的变化规律也都与轮距类似，前轮定位参数变化越小，将越有利于提高汽车的操纵稳定性。

图6为某车型前悬麦弗逊悬架实测参数输入的计算结果。图中的几组曲线是摆臂长度L取不同值的悬架运动特性。

图6 麦弗逊悬架运动特性

1.3.2 纵倾中心

麦弗逊的纵倾中心可由点T作减振器轴线垂直线。该垂线与摆臂前、后内点连线延长线的交点O即为纵倾中心(见图7)。

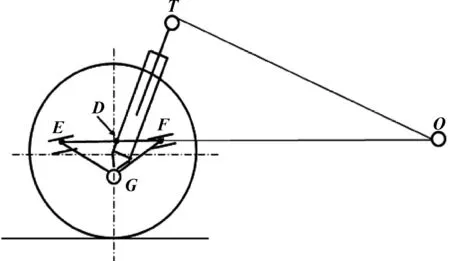
图7 麦弗逊的纵倾中心

在给定纵倾中心O位置时，结合已知的减振器上点T、摆臂外点G、等效摆臂内点D，可以通过图8方式确定摆臂前、后内点。

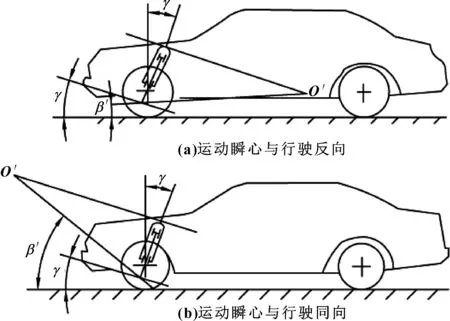
图8 运动瞬心

麦弗逊悬架的摆臂前、后内点连线与主销后倾角的匹配，影响汽车的纵倾稳定性。图8中，点O′为汽车纵向平面内悬架相对于车身跳动的运动瞬心。当摆臂前、后内点连线与地面形成的夹角-β′等于静平衡位置的主销后倾角γ时，摆臂前、后内点连线正好与主销轴线垂直，运动瞬心交于无穷远，主销轴线在悬架跳动时作平动。因此，γ值保持不变。

当β′与γ的匹配使运动瞬心O′交于前轮后方时[见图8(a)]，在悬架压缩行程中，γ有增大的趋势。当β′与γ的匹配使运动瞬心O′交于前轮前方时[见图8(b)]，在悬架压缩行程中，γ有减小的趋势。

为了减小汽车制动时的纵倾，一般希望在悬架压缩行程主销后倾角γ有增加的趋势。因此，在设计麦弗逊悬架摆臂前、后内点时，应选择参数β′能使运动瞬心O′交于前轮后方，并略为高于轮心，起到较好的抗点头作用，如果太高也不好，纵向舒适性会变差，冲击感会放大。

2 转向布置

2.1 转向断开点选定

麦弗逊悬架的转向梯形为断开式，它的优点是与前轮悬架配合，能够保证一侧车轮上、下跳动时，不会影响另一侧车轮。

转向拉杆外点可根据转向拉杆外球销与轮辋之间间隙确定(全转向时拉杆球销到轮辋、平衡块等距离在10 mm以上)，通过麦弗逊悬架图解法确定拉杆内点位置，如图9所示。

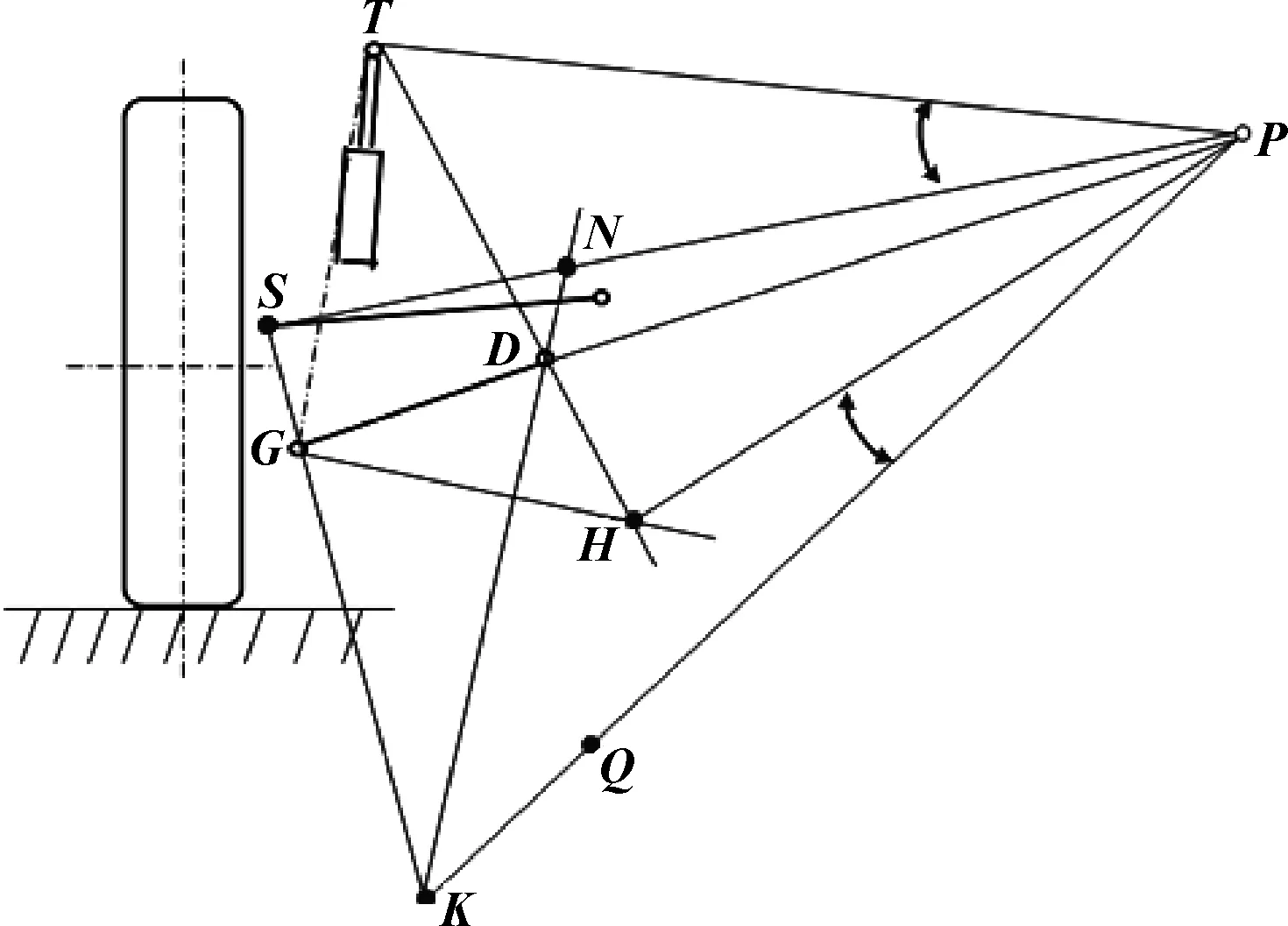
图9 转向断开点的确定

具体方法如下：

(1)作减振器轴线TG的垂直线TP，延长GD交TP于点P；

(2)过点G作GH平行于TP，连接TD并延长交GH于点H；

(3)作直线PQ，使夹角∠QPH=∠TPS；

(4)连接SG并延长交直线PQ于点K，连接KD并延长交直线SP于点N，点N便是转向横拉杆内点(断开点)的理想位置。

利用图解法能确定转向拉杆内点横向、高度(Y、Z)坐标值。转向拉杆内点的纵向(X)坐标，可通过转向拉杆轴线与转向器轴线，在全转向时所形成的锐角不小于5°来确定(考虑间隙要求，运动件与转向器间隙在15 mm以上)。转向拉杆内、外点的位置对阿克曼百分比的影响特别敏感，因此在布置转向拉杆内、外点时需要反复验证、校核。

2.2 转弯校核

汽车转弯时理论上要求4个车轮的平面垂线都相交于一点M(见图10)，这时在车身内外侧的前轮上出现不同的转向角δi和δAa。若已知内侧车轮转向角δi，即可以算出外侧车轮的理论值。

(3)

式中：L为轴距；J为两主销轴线延长线与地面交点之间的距离，J=bv-2rs，计算J时，注意主销偏移距rs有正负之分。

已知ΔδAa可通过公式算出理论转弯直径Ds，即外轮以最大的转向角转弯时经过的圆弧直径。在设计时汽车的转弯直径应尽可能的小，使得转弯及停车方便(转弯直径受轴长短距影响)。

(4)

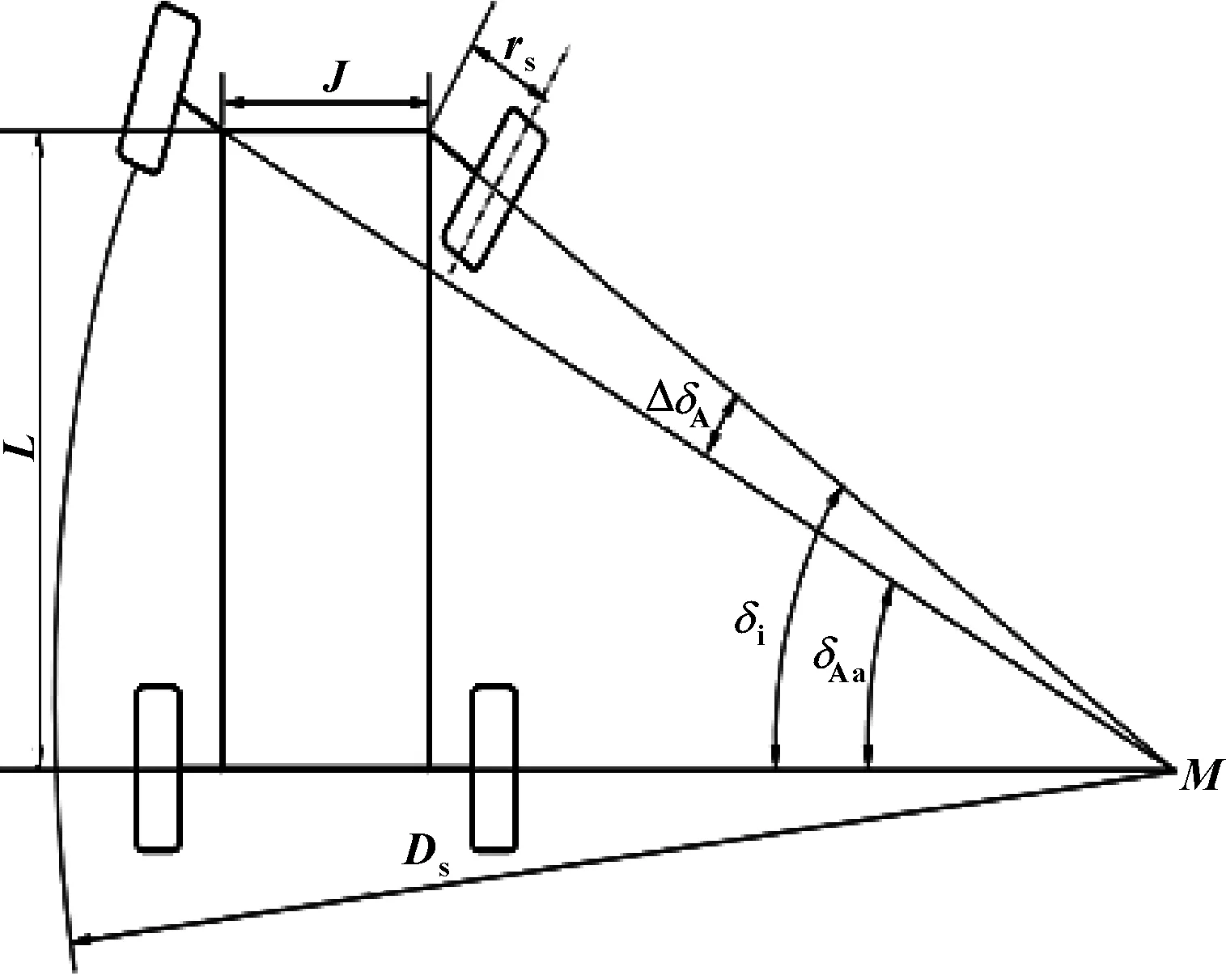
图10 车轮内、外转角之间的关系

以上公式计算出的结果均为理论值，实车计算的值都会比理论值大，因此有了阿克曼百分比Δδ

(5)

阿克曼百变比Δδ的范围一般为55%～70%，如果阿克曼百分比过小，将会导致车辆低速回正很差。

2.3 齿条行程

在确定转向拉杆内、外点，已知最大内、外轮转角的情况下可以通过作图方法(见图11)得出齿条行程大小。

图11 内外轮转角确定齿条行程

假设左右车轮转向时，转向拉杆SN与OM长度不变。齿条NM长度不变，只能左右移动。分别向右、向左全转向得出齿条位置N1M1与N2M2。则2倍N1N2或2倍M1M2的距离就是齿条行程。在实车中由于转向拉杆是空间倾斜且车轮是与主销轴线旋转，因此作图法得到的齿条行程与实际存在一定误差。在设计时可借用UG/Motion、ADAMS等软件来确定齿条行程。

3 螺旋弹簧布置

对于麦弗逊悬架来说，减振器上支点作用力方向与减振器轴线不重合，从而形成对减振器活塞杆的侧向弯曲载荷，引起减振器外筒与活塞杆导向套间的内部摩擦。当活塞改变运动方向时内部摩擦力的方向也将改变，这将导致力的突变，并将冲击传递到车身，从而影响了整车的平顺性能。

为解决减振器受力问题，弹簧的布置方式尤为重要。弹簧布置形式可以采用弹簧轴线与减振器轴线偏移一定距离、倾斜弹簧轴线与减振器轴线形成一定夹角的方法，削减及消除减振器活塞杆与导向套的摩擦。即布置弹簧时轴线尽量趋向减振器上支点作用力方向，尽可能使螺旋弹簧完全承受力。

在麦弗逊悬架中，弹簧上点一般在减振器轴线上，弹簧上点到减振器上支撑点T的距离由减振器上安装衬套及轴承大小等决定。确定弹簧上点后，根据给定空载时弹簧长度及悬架受力情况来确定弹簧下点，空载时弹簧长度一般为150～220 mm(空载弹簧长度不是弹簧自由长度)。

4 横向稳定杆布置

稳定杆布置时要求稳定杆结构形式尽可能简单化，原因是不同结构形式的稳定杆在计算扭转刚度时都是不一样的，且结构越复杂，理论计算出的扭转刚度与实际刚度相差越大。实车稳定杆为避让其他零件，通常做成比较复杂的结构形状。为简化计算，一般认为横向稳定杆是等臂梯形，且假定在车身侧倾时其力臂无变化。

麦弗逊悬架的稳定杆拉杆位置，会影响轮跳的悬架运动学特性，一般用UG/Motion、ADAMS进行拉杆运动包络分析。稳定杆具体的刚度计算用CAE进行模拟更加准确。

5 驱动轴布置

驱动轴内点主要由主减速器位置决定，驱动轴外点到车轮中心点在轮心平面的轴线距离要求为50～60 mm，最大不能超过75 mm(与轮心处的主销偏移距相关)。在布置驱动轴时，要求驱动轴内点在外点前，在俯视图中驱动轴与汽车横向轴线夹角一般在1°～2°之间，且驱动轴在空间上与整车横向轴线夹角小于6°。驱动轴工作角度过大主要影响：

(1)直接影响左右外球笼寿命(工作角度增加，球笼寿命减小)；

(2)导致内球笼轴向力增大，振动加大，NVH变差；

(3)夹角越大，三销节轴向滑移量越大，三销节磨损加剧，寿命降低、NVH越差。

6 布置校核

根据所得的硬点坐标值建立UG运动仿真模型，运用UG运动仿真模型可以检验轮心在X、Y方向的位移变化量(即轮距变化量)，及外倾角、前束角变化量是否在合理范围内。若达不到要求，需重新调整硬点直至达到要求。通过建立ADMAS动力学模型进一步验证动力性能，直至性能达到要求。

表1为麦弗逊悬架布置校核情况。

表1 麦弗逊悬架布置校核

基于布置硬点绘制零件结构，要求各零件间安装连接及拆装方便，并检查悬架上下跳及上下跳全转向时各部件间的间隙是否符合要求。若性能达到要求但间隙不符合，则可牺牲部分性能使间隙达到要求。

7 底盘模块化应用

底盘模块化设计是在一定范围内对底盘相同功能、不同性能、不同规格的零部件进行功能分析的基础上，划分并设计出一系列功能模块，通过功能模块的选择和组合构成不同的底盘产品，以满足市场的不同需求。文中以发动机横置布置的麦弗逊悬架为例，描述前悬系统模块化布置架构。

图12为某乘用车平台的前悬系统模块，该平台前悬系统采用模块化设计，适用于轿车、MPV、SUV等几款车型。该模块可以容纳1.0、1.2 L涡轮增压发动机，1.2、1.5 L发动机，并配备了4款普通变速器、2款手自一体变速器，适用4款不同型号车轮，以满足不同车型的要求。

图12 某乘用车前悬系统模块

该模块左右大梁之间用于容纳几款发动机，因此共用的前大梁主体必须按照尺寸最大的动力总成进行布置，并充分考虑其他几款动力总成的空间需求。由于该模块配备了不同型号车轮，在车轮转角相同的情况下，转向时车轮的运动空间需求不同，限制了大梁Y向间距，因此在Y向空间受限情况下，允许转向器采用不同的齿条行程，得到不同的车轮转角，满足车轮的运动空间要求。

图13为该麦弗逊悬架模块架构。

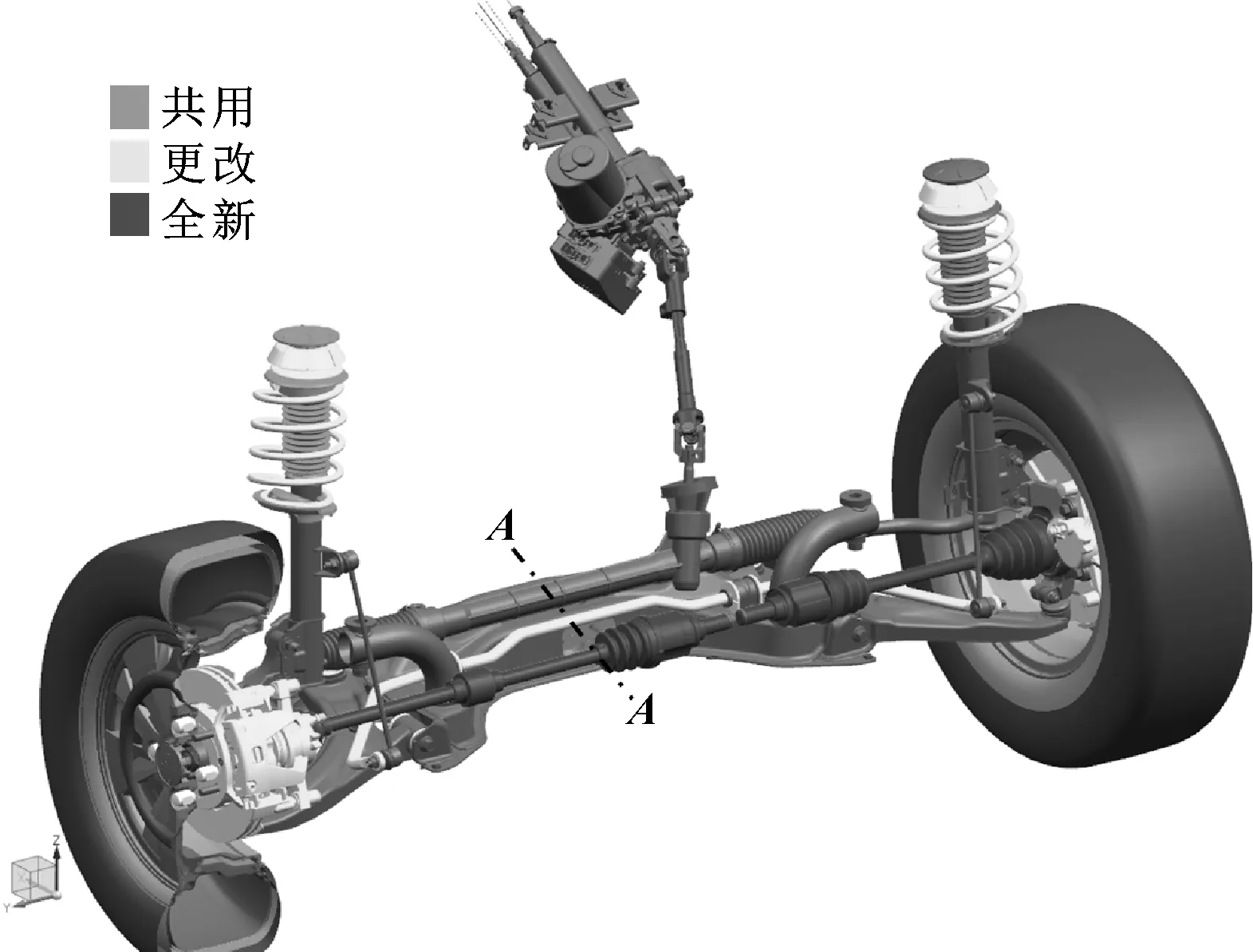
图13 前悬麦弗逊悬架系统

其主要特点为：

(1)车轮安装面相同，但采用了不同的车轮及车轮偏距ET(35～50 mm)，使得轮距也产生了变化，从而在一定程度上满足不同车型车宽的要求。但由于车轮偏距限制，这种架构方案的轮距变化范围不大，同时由于车轮宽度变化也不大，因此车宽的变化也受到限制，但为了使得轮距得到更大的变化，可以在A-A处截断拉开，但需要注意由此引起的侧倾中心的变化。

(2)该麦弗逊悬架模块采用了相同的轮毂轴承、转向节，因此制动器、车轮的安装尺寸需要保持一致，同时值得注意的是车轮中心与轮毂轴承中心之间的偏置距与轮毂轴承寿命之间的关系。

(3)制动器跟整车的制动匹配相关，稳定杆与整车的侧倾控制相关，弹簧与整车姿态、车辆轴荷相关，橡胶衬套等均需要做出相应的更改调整，但其安装尺寸尽量保持一致。

(4)驱动轴主要是由所配备的动力总成所决定。

(5)由于不同车型驾驶员位置及坐姿不同，造成方向盘的位置不相同，该模块通过转向传动轴巧妙的布置设计，实现了转向器及转向管柱共用，最大限度地实现了模块化设计。

8 结论

文中对麦弗逊悬架平台化进行研究与分析，提出开发车型采用整体模块化设计思路，并根据所搭建的不同底盘，满足整车设计的各种参数。同时在早期评估底盘设计的潜在风险，并制定相对应的解决方法。缩减了新车型的底盘开发周期，保证了资源。