某滑移门车门把手力研究

刘琳，赵宇馨，季晓丽

(泛亚汽车技术中心有限公司，上海 201201)

0 引言

汽车滑移门设计要进行虚拟耐久性试验[1]，即运用现代CAE技术搭建一个整车结构的混合多体动力学理论模型，把一些典型工况和路面特征作为输入载荷施加到虚拟试验模型上，结合各种材料的疲劳数据得到相应零部件理论疲劳损伤值，预测其疲劳寿命。

但该输入载荷具体多大，如何得到该载荷，本文作者通过特定工装，收集一批量客户的实际关门数据，并对数据进行分析处理，得到力的加载曲线，为更准确地进行CAE耐久分析提供依据。

1 测量工装

根据客户关门时把手的受力情况，设计了一个外观与车门外把手造型基本一致的工装来测作用力。在工装的前后方向和里外方向各布置了一个三向的传感器，可以精确地收集开关门时客户作用在把手上的力。测量工装如图1所示。

2 关门试验数据处理

试验共采集了31组关门数据，数据处理如下：

(1)对试验数据进行低通滤波，截止频率为100 Hz。

(2)取前、后传感器在Fx方向的绝对值进行相加作为门把手在Fx方向合力的大小，门把手在Fy和Fz向的合力也采用同样的方法处理，见图2。

图1 测量工装

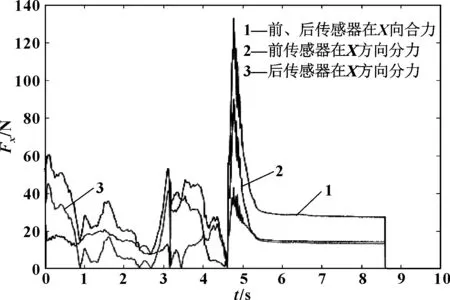
图2 前、后传感器的X向分力及合力

在MATLAB中对每组驱动力数据进行滤波降噪[2]处理，初步统计各组驱动力数据的持续加载时间、最大值、平均值，如表1所示。

表1 关闭驱动力初步统计结果

2.1 持续时间分布检验

(1)统计描述

利用spss[3]，对31个样本的持续时间进行统计描述，如表2所示。

表2 持续时间统计

可知，样本的平均持续时间为1.387 5 s，去掉两侧各5%的极端值后，截尾均数为2.002 9 s，中位数为1.418 s，从上述指标即可推测出数据不存在极端值且为对称分布。持续时间的方差为0.073，标准差为0.269 95 s。最短持续时间为0.77 s，最长持续时间为2.04 s。根据偏度及峰度系数可推断出常速关闭驱动力持续时间分布为正偏态，较陡峭；95%的人作用在门把手力持续时间为1.288 5～1.486 5 s。

(2)分布检验

分别采用Kolmogorov-Smirnov检验(柯尔莫可洛夫-斯米洛夫检验，K-S检验)[4]、Shapiro-Wilk检验(夏皮罗-威尔克检验，W检验)，判断样本是否服从正态分布，如表3所示。

表3 持续时间分布检验

注：a为里利氏显著性修正。

因样本含量较少，应以W检验结果为准。由表3可知，其显著性为0.805>0.05，因此持续时间服从正态分布。

(3)图示验证

绘制持续时间与频数的直方图，对结果进行验证，如图3所示。

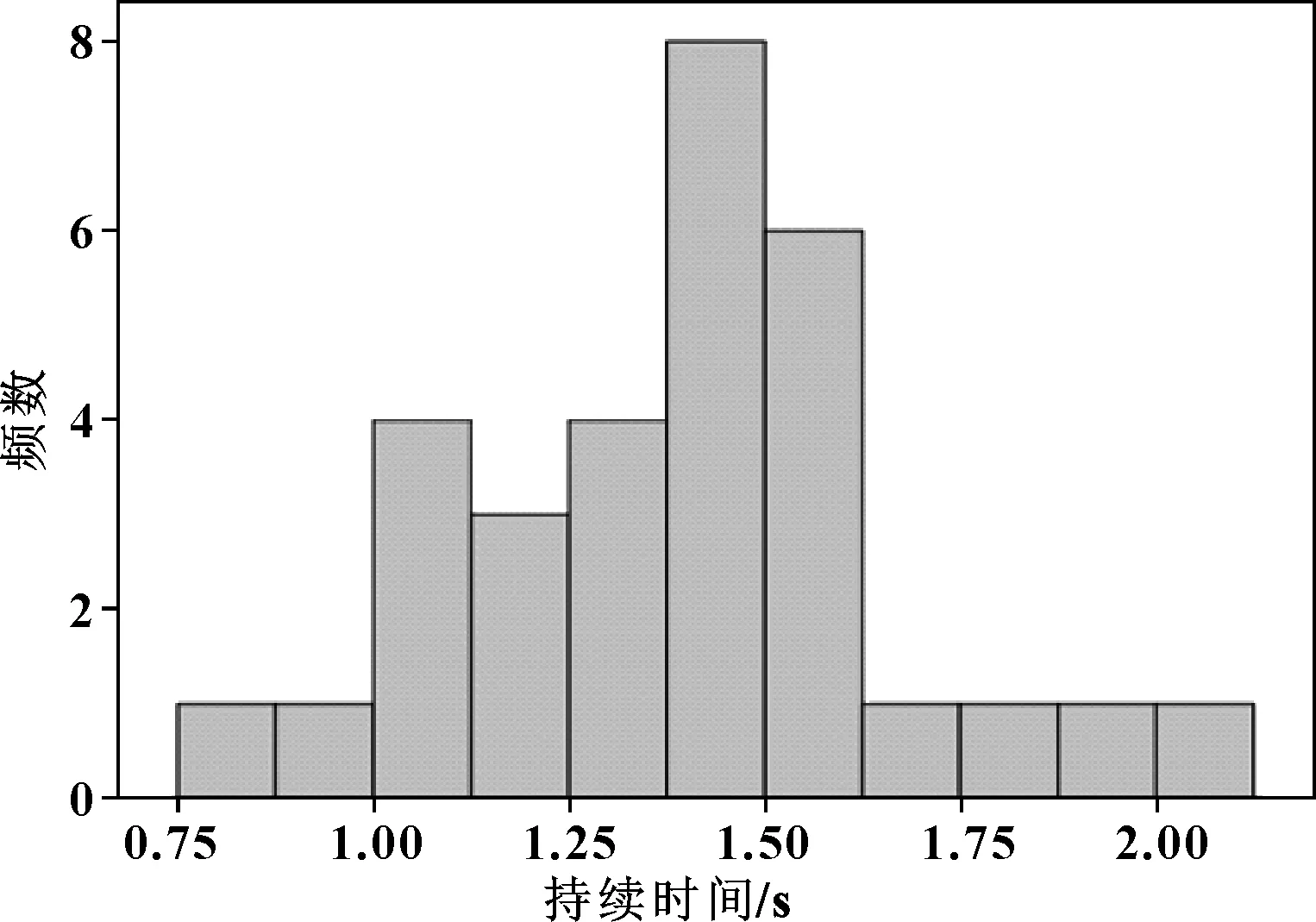
图3 持续时间与频数的直方图

可知，持续时间服从N(1.387 5,0.269 952)的正态分布。

2.2 驱动力最大值分布检验

由于客户在开关门过程中只在X方向做功，所以分析数据时只需考虑X方向的驱动力。根据X向驱动力的结果确认最具代表性的加载力，从而确认X/Y/Z方向的驱动力大小。

(1)统计描述

利用spss，对31个样本的驱动力最大值进行统计描述，如表4所示。

表4 X向驱动力最大值统计

可知，31个样本的X向驱动力Fx最大值的平均值为46.967 8 N，去掉两侧各5%的极端值后，截尾均数为46.111 5 N，中位数为46.090 6 N，从上述指标即可推测出数据不存在极端值且为对称分布。X向驱动力最大值的方差为205.698，标准差为14.342 16 N。最小的力最大值为25.87 N，最大为88.73 N。根据偏度及峰度系数可推断出X向驱动力Fx最大值分布为正偏态，较陡峭；95%的人作用在门把手X向驱动力Fx最大值为41.707～52.228 5 N。

(2)分布检验

分别采用Kolmogorov-Smirnov检验(K-S检验)、Shapiro-Wilk检验(W检验)，判断样本是否服从正态分布，如表5所示。

表5 X向驱动力最大值分布检验

注：a为里利氏显著性修正。

因样本含量较少，应以W检验结果为准。可知，其显著性为0.188>0.05，因此X向驱动力Fx最大值服从正态分布。

(3)图示验证

绘制X向驱动力最大值与频数的直方图对结果进行验证，如图4所示。

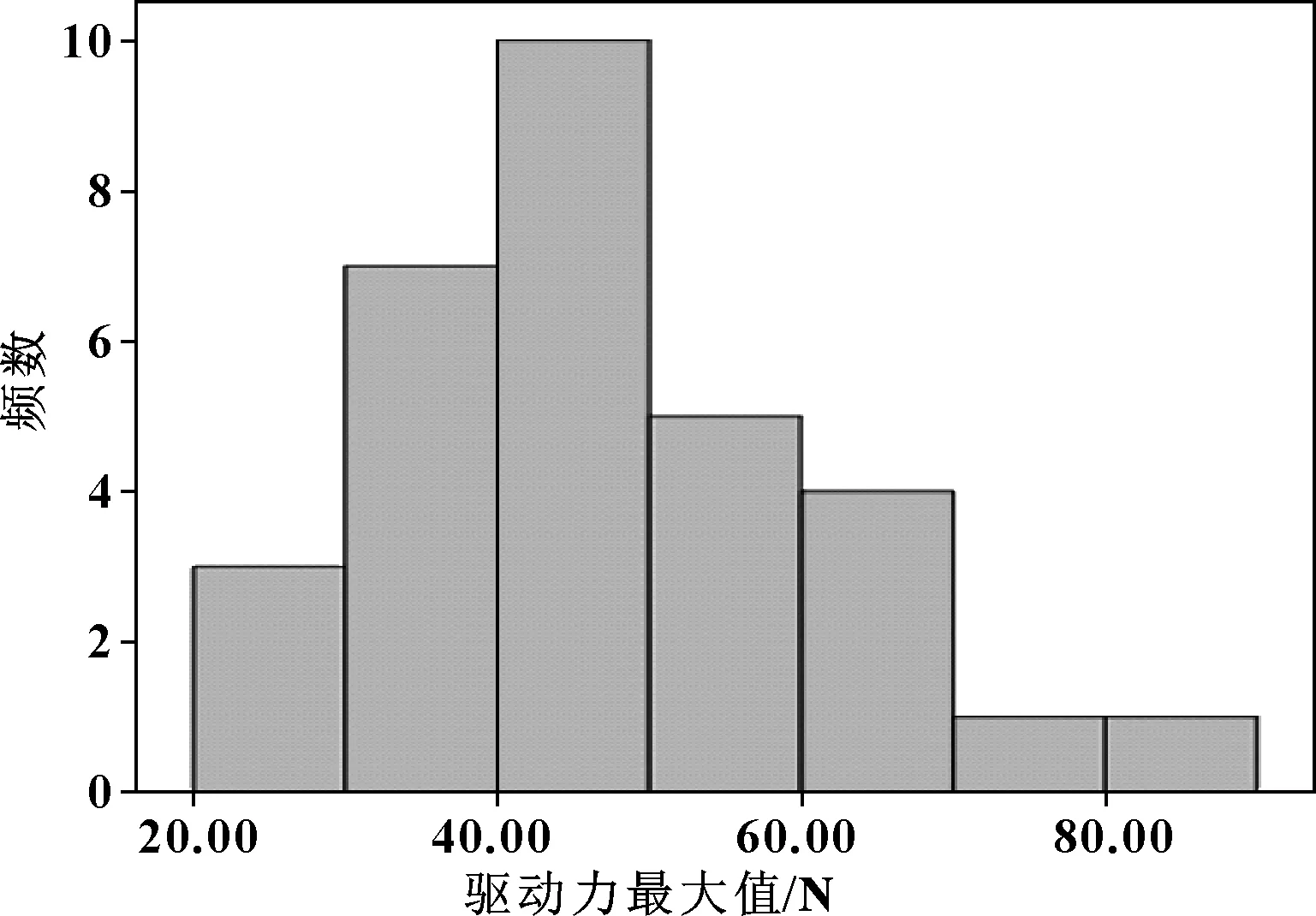
图4 X向驱动力最大值与频数的直方图

可知，驱动力最大值服从N(46.967 8, 14.342 162)的正态分布。

2.3 驱动力平均值分布检验

(1)统计描述

利用spss，对31个样本的驱动力平均值进行统计描述，如表6所示。

表6 X向驱动力平均值统计

可知，31个样本的X向驱动力Fx平均值的均值为28.072 1 N，去掉两侧各5%的极端值后，截尾均数为27.855 9 N，中位数为27.911 4 N，从上述指标即可推测出数据不存在极端值且为对称分布。X向驱动力平均值的方差为56.302，标准差为7.503 44 N。最小的力平均值为15.85 N，最大为43.65 N。根据偏度及峰度系数可推断出X向驱动力Fx平均值分布为正偏态，较平坦；95%的人作用在门把手X向驱动力Fx平均值为25.319 8～30.824 3 N。

(2)分布检验

分别采用Kolmogorov-Smirnov检验(K-S检验)、Shapiro-Wilk检验(W检验)，判断样本是否服从正态分布，如表7所示。

表7 X向驱动力平均值分布检验

注：a为里利氏显著性修正。

因样本含量较少，应以W检验结果为准。可知，其显著性为0.172>0.05，因此X向驱动力Fx平均值服从正态分布。

(3)图示验证

绘制X向驱动力平均值与频数的直方图对结果进行验证，如图5所示。

图5 X向驱动力平均值与频数的直方图

可知，驱动力平均值服从N(28.072 1, 7.503 442)的正态分布。

2.4 主成分分析

实际工作中，为了全面系统地反映问题，往往收集的变量较多，但这样就会经常出现所收集的变量间存在较强相关性的情况。这些变量间存在着较多的重复信息，直接用它们分析现实问题，不但模型复杂，还会因为变量间存在的多重共线性而引起极大的误差。

为了能够充分而有效地利用数据，通常希望用较少的新指标代替原来较多的旧变量，同时要求这些新指标尽可能地反映原变量的信息。主成分分析和因子分析正是解决此问题最有效的多元统计方法，它们能够提取信息，使变量简化降维，从而使问题更加简单直观。

主成分分析[5]是考察多个变量间相关性的一种多元统计方法。它是研究如何通过少数几个主分量来解释多个变量间的内部结构。也就是说，从原始变量中导出少数几个主分量，使它们尽可能多地保留原始变量的信息，且彼此间互不相关。主成分分析的应用目的可以被简单归结为：数据的压缩、数据的解释。它常被用来寻找判断某种事物或现象的综合指标，并且对综合指标所包含的信息给以适当的解释，从而更加深刻地揭示事物的内在规律。

对描述驱动力加载方式的3个变量进行主成分分析，得到各变量间的相关系数矩阵，如表8所示。

表8 驱动力描述变量相关性矩阵

可知，许多变量之间直接的相关性比较强，的确存在信息上的重叠。

表9是各成分的方差贡献率和累计贡献率。可知，只有前2个特征根大于1，因此只提取了前2个主成分。

表9 各成分的方差贡献率与累计贡献率

第一个主成分的方差占所有主成分方差的62.647%，超过一半，前两个主成分的方差贡献率达到96.217%，因此选前两个主成分已足够描述驱动力的普遍加载规律。

3 结论

根据前述各变量的分布检验结果及主成分提取结果，可以得出：某一速度下关门力的持续加载时间服从N(1.387 5,0.269 952)的正态分布，驱动力最大值服从N(46.97, 14.342 1)的正态分布。据此可从31组样本中选取最具代表性的驱动力加载方式，如图6所示(样本编号947.rsp)。

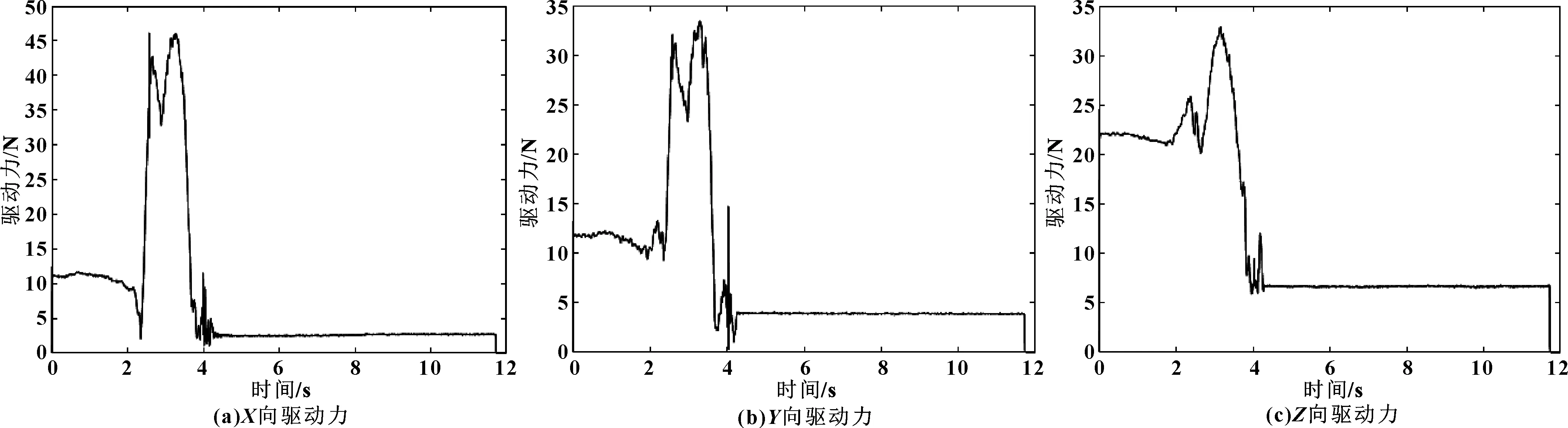
图6 样本编号947.rsp驱动力