Cn×P2的符号全控制数与符号全加强数
李宁,范英梅
(广西大学数学与信息科学学院, 广西南宁530004)
0 引言
自从ZELINKA[1]提出符号全控制数(signed total domination number)的概念以来,已经有很多学者对符号全控制数给出了深入的研究[2-5]。令G=(V(G),E(G))是一个无孤立点的简单无向图,其顶点集和边集分别用V(G)和E(G)表示。定义图G中的任意一个顶点v∈V(G)的开邻集为NG(v) = {u∈V(G)|uv∈E(G)},闭邻集为NG[v]=NG(v)∪{v}。顶v∈V(G)的度为dG(v)=|NG(v)|,最大度为Δ(G)=max{dG(v)|v∈V(G)},最小度为δ(G)=min{dG(v)|v∈V(G)}。如果Δ(G)=δ(G)=r,则称G是r-正则的。对于任意S⊆V(G),NG(S)=∪v∈SNG(v),NG[S]=NG(S)∪S。对图G的任意两个子集A,B⊆V(G), 定义E(A,B) = {e=xy|x∈A,y∈B}、e(A,B) = |E(A,B)|。
无向图G= (V,E),f:V→R是定义在顶点集V(G)上的实函数。f的权重定义为ω(f)=∑v∈Vf(v)。对于顶点集的任意一个子集S⊆V,定义f(S)=∑v∈Sf(v),那么,ω(f) =f(V) 。如果函数f:V(G)→{-1,1}可以让图G上任意顶点v∈V满足f(N(v))≥1,那么本文称这个函数f是定义在V(G)上的符号全控制函数 (signed total dominating function, STDF)。图G的符号全控制数定义为γst(G)=min{ω(f)|f是图G的一个STDF}。
作为研究图的稳定性的一个重要参数,图G的加强数是由 KOK等[6]首次提出来的, 并且得到了很多很好的结论。在文献[7]中,给出了图G的符号全加强数(signed total reinforcement number)的定义:对于Ec(G)中的任意一子集S, 使得不等式γst(G+S) <γst(G)成立的最小的集合S的势。使得γst(G+S)<γst(G)成立的最小的边集合S成为图G的符号全加强数集(signed total reinforcement set)。对符号全控制数和符号全加强数,学者们已经给出了很多成果[5,8-10]:
引理1定义在图G的顶点集上的符号全控制函数f是极小的当且仅当对于顶点集上的任意一个满足f(v) = 1的顶点v∈V,均存在u∈N(v),使得f[u]=f(N[u])∈{1,2}[5]。
引理2r-正则图G的阶n≥3,则当r为奇数时γst(G)≥n/r;当r为偶数时γst(G)≥2n/r[5]。
引理3阶为n的图G,其最小度δ≥2,则[5]:
对于任意两个无孤立点的无向图G和H,它们的乘积图是以V(G)×V(H) 作为顶点集。两个顶点(u1,v1)和(u2,v2)之间若存在一条边当且仅当u1=u2且v1v2∈E(H)成立,或者v1=v2且u1u2∈E(G)成立。记G和H的乘积图为G×H。
本文给出Cn×P2(n≥3)符号全控制数和符号全加强数。以下章节中,下标中的加减运算均使用mod(n)运算规则。
1 Cn×P2 的符号全控制数
令f是定义在Cn×P2上的一个最小STDF且记P=f-1(1)、M=f-1(-1)。由Cn×P2是3-正则图知:
性质1对任一顶点v,均成立|N(v)∩M|≤1。
证明本文记|N(v)∩M|=N-,|N(v)∩P|=N+,则由符号全控制数的定义可得:1≤f(N(v)) =N+-N-=deg(v)-2N-=3-2N-。因此N-≤1,故结论成立。
性质2Cn×P2中
证明由性质1可知:则对任一M集中的点v,均成立|N(v)∩M|≤1。故结论成立。
性质3如果存在M中的一个点v使得N(v)∩M=φ,则{u∈V|d(u,v)=1或2}⊆P。
证明对任意w∈{u∈V|d(u,v)=1或2},如果d(w,v)=1,则由N(v)∩M=Φ可知,w∈P。如果d(w,v)=2且f(w)=-1,则对于N(v)和N(w)的公共交点x,成立f(N(x))≤f(w)+f(v)+1<0。矛盾。故假设不成立,所以w∈P,结论成立。
性质4对于任意无孤立点的无向图G,如果存在图G的补图的子集A,使得不等式γst(G+A)<γst(G)成立,那么γst(G+A)≤γst(G)-2。
证明令函数f和函数g分别数图G+A和图G的最小符号控制函数, 并且分别记f-1(a)和g-1(a)为值a在函数f和函数g下的原像。因为γst(G+A)<γst(G),所以|f-1(1)|≤|g-1(1)|-1。 也就是说|f-1(-1)|≥|g-1(-1)|+1。因此:γst(G+A)=|f-1(1)|-|f-1(-1)|≤|g-1(1)|-|g-1(-1)|-2=γst(G)-2。

证明由定义知Cn×P2就是Petersen图P(n,1),故可令U= {u1,u2,…,un}和V={v1,v2,…,vn}是它的内外层点集,显然它们各自构成一个长n的圈。
情形1n=3k(k∈N+)或n=3k+1(k∈N+)。

由Cn×P2是3-正则图及引理2可知,γst(Cn×P2)≥|V(Cn×P2)|/3=2n/3。
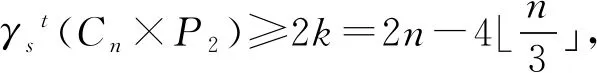


情形2n=6k+5(k∈N)。
在Cn×P2上定义一个函数f:当x∈{v1,v2,u4,u6,…v6k-5,v6k-4,u6k-2,u6k-1,v6k+1,v6k+2,u6k+4}时,f(x)=-1;否则f(x)=1。易验证对于任意一顶点x,均成立f(N(x))≥1。所以f是定义在Cn×P2上的STDF且γst(Cn×P2)≤f(V(Cn×P2))=4k+4。
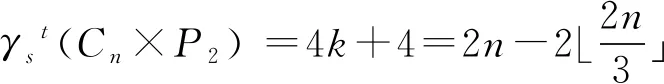
情形3n=6k+2(k∈N+)。
在Cn×P2的顶点集上定义一个函数f如下:当x∈{v1,u1,v4,u4,…v6k-5,u6k-5,v6k-2,u6k-2}时f(x)=-1,其余情况下f(x)=1。易验证对于任意一顶点x,均成立f(N(x))≥1。所以f是定义在Cn×P2上的STDF且γst(Cn×P2)≤f(V(Cn×P2))=4k+4。
由Cn×P2是3-正则图及引理2知,γst(Cn×P2)≥|V(Cn×P2)|/3=4k+1+1/3。因此,4k+4≥γst(Cn×P2)≥4k+2。同理情形 1,可以断言γst(Cn×P2)是偶数,所以γst(Cn×P2)= 4k+2或者4k+4。
假设γst(Cn×P2)= 4k+2。令g是定义在C6k+2×P2上的一个最小STDF且记P=g-1(1)、M=g-1(-1),则由γst(Cn×P2)= 2n-2|M|可得|M|=4k+1。

2 Cn×P2 的符号全加强数
引理4若n=3k+1(k∈N+),则Rst(Cn×P2)=3。
证明记G′=Cn×P2+vnvn-2+vnun-1+vn-2un-1,则在G′上定义一个函数g如下:当x∈{v1,u1,…v3k-2,u3k-2,v3k}时g(x)=-1,其余情况下g(x)=1。易验证g是定义在G′上的STDF且γst(G′)≤g(V(G′))=2k<2k+2=γst(Cn×P2)。故Rst(Cn×P2)≤3。本文只需证明Rst(Cn×P2)≥3即可得到结论。
反证假设存在不同的e1,e2∈Ec(Cn×P2)(记G′=Cn×P2+e1+e2)使得γst(G′)<γst(Cn×P2)。由性质4知γst(G′)≤2k。令φ是定义在V(Cn×P2+e1+e2)的一个最小STDF且记P=φ-1(1)、M=φ-1(-1),则由γst(G′)=ω(φ)=|P|-|M|≤2k及|P|+|M|=2(3k+1)可得:|P|≤4k+1,|M|≥2k+1。
情形1若e1和e2无交点,则δ(Cn×P2+e1+e2)=3且Δ(Cn×P2+e1+e2)=4,由引理3可知γst(Cn×P2+e1+e2)≥2(3k+1)/3=2k+2/3。所以γst(Cn×P2+e1+e2)≥2k+1。因为γst(Cn×P2+e1+e2)=2n-2|M|是偶数,所以γst(Cn×P2+e1+e2)≥2k+2。矛盾。
情形2若e1和e2有一个公共交点,本文记为x,则可以令e1=xy,e2=xz。
①x,y,z∈M,则e(M,P)≥2(|M|-3)+e(x,P)+e(y,P)+e(z,P)≥2(|M|-3)+3+3+3= 2|M|+3≥ 4k+5;e(P,M)≤|P|≤4k+1。矛盾。
②x,y,z中有且仅有2个在M中,本文仅需考虑两类:
若x,y∈M且z∈P(由对称性,和x,z∈M且y∈P一样),则e(M,P)≥2(|M|-2)+e(x,P) +e(y,P)≥2(|M|-2)+3+3=2|M|+2≥4k+4;e(P,M)≤|P|≤4k+1。矛盾。
若y,z∈M且x∈P,则e(M,P)≥2(|M|-2)+e(y,P)+e(z,P)≥2(|M|-2)+3+3=2|M|+2≥4k+4;e(P,M)≤(|P|-1)+e(x,M)=(|P|-1)+2≤4k+2。矛盾。
③x,y,z中有且仅有1个在M中。由对称性,本文仅需考虑以下两种情况
若x∈M且y,z∈P,则e(M,P)≥2(|M|-1)+e(x,P)≥2(|M|-1)+3=2|M|+1≥4k+3;e(P,M)≤ (|P|-2)+e(y,M)+e(z,M)≤|P|-2+1+1=|P|≤4k+1。矛盾。
若y∈M且x,z∈P(由对称性,和z∈M且x,y∈P一样),则e(M,P)≥2(|M|-1)+e(y,P)≥2(|M|-1)+3=2|M|+1≥4k+3;e(P,M)≤(|P|-2)+e(x,M)+e(z,M)≤|P|-2+2+1=|P|+1≤4k+2。矛盾。

综上所示,假设不成立。故结论成立。

证明 情形1若k为偶数,则本文可以令n=6t+2。
此时γst(Cn×P2)=4t+4。记G′=Cn×P2+vnvn-2+vnun-1,则在G′上定义一个函数φ如下:
下面来着重说一下我的这幅《乐园》的具体创作过程,主要包括构图、色彩、线条、肌理效果、展出方式。这幅作品的尺寸为100cm*200cm,采用的是毛毡材料拼贴的方式。

易验证对φ是定义在G′上的STDF且γst(G′)≤φ(V(G′))=4k+2<4k+4=γst(Cn×P2)。故Rst(Cn×P2)≤2。本文仅需证明Rst(Cn×P2)≥2即可得结论。
反证假设存在e∈Ec(Cn×P2)使得γst(Cn×P2+e) <γst(Cn×P2)= 4t+4,则由性质4可知γst(Cn×P2+e)≤4t+2。
由引理3及δ(Cn×P2+e)=3<4=Δ(Cn×P2+e)可得γst(Cn×P2+e)≥2(6t+2)/3=4t+1+1/3,也即γst(Cn×P2+e)≥4t+2,所以γst(Cn×P2+e)=4t+2。令φ是定义在Cn×P2+e上的一个最小STDF且记P=φ-1(1)、M=φ-1(-1),则由γst(Cn×P2+e)=ω(φ)=|P|-|M|=4t+2及|P|+|M|=2(6t+2)可得:|P|=8t+3,|M|=4t+1。
记e=xy,则在Cn×P2+e中,由Δ(Cn×P2+e)=4可知:对于任一点v∈V(Cn×P2+e),为保证φ(N(v))≥1,必有|N[v]∩M|≤2。由性质2可知
① 若x,y∈M,则e(M,P)≥2(|M|-2)+e(x,P)+e(y,P)=2(|M|-2)+3+3=8t+4,e(P,M)≤|P|=8t+3。矛盾。
② 若x,y中有一个点属于M,则由对称性我们可以令x∈M且y∈P。
若x在

综上所示,假设不成立。故结论成立。
情形2若k为奇数,令n=6t+5,则γst(Cn×P2)=4t+4。
记G′=Cn×P2+u1vn+u2vn+u1vn-1,则在G′上定义一个函数φ如下:
易验证φ是定义在G′上的STDF且γst(G′)≤φ(V(G′))=4k+2<4k+4=γst(Cn×P2)。故Rst(Cn×P2)≤3。现在仅需证明Rst(Cn×P2)≥3即可得结论。
反证假设存在不同的e1,e2∈Ec(Cn×P2)使得γst(Cn×P2+e1+e2)<γst(Cn×P2)=4t+4,记G0=Cn×P2+e1+e2,则由性质4知γst(G0)≤4t+2。
若e1和e2无交点,则δ(G0)=3且Δ(G0)=4,由引理3可知γst(G0)≥2(6t+5)/3=4t+3+1/3,也即γst(G0)≥4t+4。矛盾于γst(G0)≤4t+2。
若e1和e2有一个公共交点,本文记为x,则令e1=xy,e2=xz。令φ是定义在G0上的一个最小STDF且记P=φ-1(1)、M=φ-1(-1),则由γst(G0)=ω(φ)=|P|-|M|≤4t+2及|P|+|M| =2(6t+5)可得:|P|≤8t+6,|M|≥4t+4。
①x,y,z∈M,则e(M,P)≥2(|M|-3)+e(x,P)+e(y,P)+e(z,P)≥2(|M|-3)+3+3+3= 2|M|+3≥ 8t+11;e(P,M)≤ |P|≤8t+6。矛盾。
②x,y,z中有且仅有2个在M中。由对称性,可以考虑以下两种情况:
若x,y∈M且z∈P(与x,z∈M且y∈P对称),则e(M,P)≥2(|M|-2) +e(x,P) +e(y,P)≥2(|M|-2) +3 +3 =2|M|+2≥8t+10且e(P,M)≤(|P|-1)+e(z,M)=|P|-1+1≤8t+6。矛盾。
若y,z∈M且x∈P,则e(M,P)≥2(|M|-2)+e(y,P)+e(z,P)≥2(|M|-2)+3+3=2|M|+2≥8t+10且e(P,M)≤(|P|-1)+e(x,M)=(|P|-1)+2≤8t+7。矛盾。
③x,y,z中有且仅有1个在M中。由对称性,可以考虑以下两种情况:
若y∈M且x,z∈P(与z∈M且x,y∈P对称),则e(M,P)≥2(|M|-1) +e(y,P)≥2(|M|-1) +3 =2|M|+1≥8t+9且e(P,M)≤(|P|-2)+e(x,M)+e(z,M)=|P|-2+2+1≤8t+7。矛盾。
若x∈M且y,z∈P,则e(M,P)≥2(|M|-1)+e(x,P)≥2(|M|-1)+3=2|M|+1≥8t+9且e(P,M)≤(|P|-2)+e(y,M)+e(z,M)=(|P|-2)+1+1≤8t+6。矛盾。

综上所示,假设不成立。故结论成立。
引理6若n=3k(k≥2,k∈N+),则Rst(Cn×P2)=5。
证明记G′=Cn×P2+v1u2+v1v3+v3vn-1+vn-1un+unu2,则在G′上定义函数φ:

易验证对φ是定义在G′上的STDF且γst(G′)≤φ(V(G′))=2k-2<2k=γst(Cn×P2)。故Rst(Cn×P2)≤5。现在仅需证明Rst(Cn×P2)≥5即可得结论。
反证假设存在不同的e1,e2,e3,e4∈Ec(Cn×P2) (记G0=Cn×P2+e1+e2+e3+e4)使得γst(G0)<γst(Cn×P2)=2k,则由性质4知γst(G0)≤2k-2。令φ是定义在G0上的一个最小STDF且记P=φ-1(1)、M=φ-1(-1),则由γst(G0)=ω(φ)=|P|-|M|≤2k-2及|P|+|M|=2×3k可得:|P|≤4k-1,|M|≥2k+1。
情形1若e1,e2,e3,e4两两不交,则δ(G0)=3且Δ(G0)=4,由引理3可知γst(G0)≥2×3k/3=2k。矛盾于γst(G0)≤2k-2。
情形2若e1,e2,e3,e4有一个交点,则:
①e1,e2,e3,e4有一个公共交点,记为x,本文断言x∈P。否则,由定义可知e(P,M)≤|P|≤4k-1;e(M,P)≥2(|M|-1)+4≥ 4k+4。矛盾。所以对于任意v∈V(G0),必有|N[v]∩M|≤2。故|M|≤2×3k/3=2k,矛盾于|M|≥2k+1。
② 若三条交于一点,一条独立,则可记e1=xa,e2=xb,e3=xc,e4=yz。为保证f(N(x))≥1,则a,b,c中至少有一个点在P中。记A={x,y,z,a,b,c},则|A∩M|≤5。
若|A∩M|=5,由对称性讨论a∈P即可。e(P,M)≤|P|-1+e(a,M)≤4k-1;e(M,P)≥2(|M|-5) +e(x,P)+e(b,P)+e(c,P)+e(y,P)+e(z,P)≥ 4k+8。矛盾。若|A∩M|=4,由对称性讨论c,z∈P;b,c∈P;x,c∈P即可。前两者成立e(P,M)≤|P|-2+1+1≤4k-1和e(M,P)≥2(|M|-4)+4+3×3≥4k+7。x,c∈P成立e(P,M)≤|P|-2+2+1≤ 4k;e(M,P)≥2 (|M|-4) +3×4≥ 4k+6。矛盾。若|A∩M|=3。由对称性,仅需讨论x,a,b∈M;x,a,y∈M;x,y,z∈M;a,b,y∈M;a,y,z∈M。前三种情况均成立e(P,M)≤|P|-3+1+1+1≤4k-1和e(M,P)≥2(|M|-3)+4+3+3≥ 4k+6。矛盾。后二种情况均成立e(P,M)≤|P|-3+2+1+1≤4k;e(M,P)≥ 2(|M|-3)+3×3≥ 4k+5。矛盾。若|A∩M|=2。由对称性,仅需讨论y,z∈M;a,y∈M;a,b∈M;x,y∈M;x,a∈M。易验证,前三种时成立e(P,M)≤|P|-4+1+1+1+2≤4k和e(M,P)≥2(|M|-2)+3+3≥ 4k+4,矛盾。后两个成立e(P,M)≤|P|-4+4×1≤4k-1和e(M,P)≥ 2(|M|-2)+4+3≥ 4k+5。矛盾。若|A∩M|=1。由对称性,仅需讨论x∈M;a∈M;y∈M。易验证,第一种成立e(P,M)≤|P|-5+1×5≤4k-1和e(M,P)≥2(|M|-1)+4≥4k+4,矛盾。后两种成立e(P,M)≤ |P|-5+2+4×1≤4和e(M,P)≥ 2(|M|-1)+3≥ 4k+3,矛盾。若|A∩M|=0。则对任意v∈V(G0),有|N[v]∩M|≤2。故|M|≤2×3k/3=2k,矛盾于|M|≥2k+1。
③ 两条有一个公共交点,其余两条边各自独立,可以记e1=ab,e2=bc,e3=df,e4=gh。记A={a,b,c,d,f,g,h},则A⊆M不成立。否则,e(P,M)≤|P|≤4k-1和e(M,P)≥2(|M|-7)+3×7≥ 4k+9相矛盾,A⊆P也不成立。否则,对任意v∈V(G0),必有|N[v]∩M|≤2,故|M|≤2×3k/3=2k,矛盾于|M|≥2k+1。
若|A∩M|=6,由对称性知讨论a∈P;d∈P;b∈P即可。前两种时成立e(P,M)≤ |P|-1+1≤ 4k-1和e(M,P)≥2(|M|-6)+3×6≥4k+8,矛盾。最后一种成立e(P,M)≤|P|-1+2≤4k和e(M,P)≥ 2(|M|-6) +3×6≥ 4k+8。矛盾。若|A∩M|=5。由对称性仅需讨论d,g∈P;a,c∈P;a,d∈P;d,f∈P;a,b∈P;b,d∈P即可。前四种情形下成立e(P,M)≤|P|-2+1+1≤4k-1和e(M,P)≥ 2(|M|-5) +3×5≥4k+7,矛盾。后两种下成立e(P,M)≤ |P|-2+2+1≤4k和e(M,P)≥2(|M|-5)+3×5≥ 4k+7。矛盾。若|A∩M|=4,由对称性仅需讨论a,b,c∈P;a,b,d∈P;b,d,f∈P;b,d,g∈P;a,c,d∈P;a,d,f∈P;a,d,g∈P;d后四种时成立e(P,M)≤ |P|-3+1+1+1≤4k-1和e(M,P)≥2(|M|-4)+3×4≥ 4k+6,矛盾。若|A∩M|=3。由对称性仅需讨论a,b,c∈M;a,b,d∈M;b,d,f∈M;b,d,g∈M;a,c,d∈M;a,d,f∈M;a,d,g∈M;d,f,g∈M。前四种成立e(P,M)≤ |P|-4+1×4≤4k-1和e(M,P)≥2(|M|-3)+3×3≥ 4k+5,矛盾。后4种成立e(P,M)≤ |P|-4+1×3+2≤4k和e(M,P)≥2(|M|-3)+3×3≥ 4k+5,矛盾。若|A∩M|=2,由对称性仅需讨论d,g∈P;a,c∈P;a,d∈Pd,f∈P;a,b∈P;b,d∈P即可。前四种成立e(P,M)≤|P|-5+1×4+2≤4k和e(M,P)≥2(|M|-2)+3×2≥ 4k+4,矛盾。其余时成立e(P,M)≤|P|-5+5×1≤4k-1和e(M,P)≥2(|M|-2)+3×2≥ 4k+4。矛盾。若|A∩M|=1,由对称性仅需讨论a∈M;d∈M;b∈M。前2种成立e(P,M)≤|P|-6+1×5+2≤4k和e(M,P)≥ 2(|M|-1)+3×1≥4k+3,矛盾。其余成立e(P,M)≤ |P|-6+1×6≤4k-1和e(M,P)≥2(|M|-1)+3×1≥ 4k+3,矛盾。
情形 3若e1,e2,e3,e4有2个交点,则:
① 若三条交于2点,另一条独立,可以记e1=ab,e2=bc,e3=cd,e4=fg。记A={a,b,c,d,f,g}。则A⊆M不成立。否则,e(P,M)≤|P|≤4k-1且e(M,P)≥2(|M|-6)+3×6≥ 4k+8。矛盾。A⊆P也不成立,否则对任意v∈V(G0),有|N[v]∩M|≤2。故|M|≤2×3k/3=2k,矛盾于|M|≥2k+1。
若|A∩M|=5,由对称性仅需讨论a∈P;g∈P;b∈P即可。前2种成立e(P,M)≤|P-1+1≤4k-1和e(M,P)≥2(|M|-5)+3×5≥4k+7,矛盾。其余成立e(P,M)≤|P|-1+1≤4k-1和e(M,P)≥ 2(|M|-5)+3×5≥ 4k+7。矛盾。若|A∩M|=4,由对称性仅需讨论g,f∈P;d,f∈P;a,d∈P;b,c∈P;c,f∈P;c,d∈P;b,d∈P。均成立e(M,P)≥2(|M|-4)+3×4≥ 4k+6。且前三种时e(P,M)≤|P|-2+1+1≤4k-1后三种时e(P,M)≤|P|-2+1+1≤4k,其余成立e(P,M)≤|P|-2+2+2≤4k+1,均矛盾。若|A∩M|=3。由对称性d,f,g∈M;a,d,f∈M;c,f,g∈M;d,f,c∈Mb,d,f∈M;a,c,d∈M;b,c,f∈M;b,c,d∈M。这些情况下均成立e(M,P)≥2(|M|-3)+3×3≥ 4k+5。前两种时e(P,M)≤|P|-2+2+2≤4k+1;后2种时e(P,M)≤|P|-3+1+1+1≤4k-1;其余时e(P,M)≤|P|-3+1+2+1≤4k。均矛盾。若|A∩M|=2。由对称性仅需讨论g,f∈M;d,f∈M;a,d∈M;c,f∈M;c,d∈M;b,d∈M;b,c∈M即可。这些情况下均成立e(M,P)≥2(|M|-2)+3×2≥ 4k+4。讨论e(P,M):前三种时e(P,M)≤|P|-4+1+2+2+1≤4k+1;后1种时e(P,M)≤ |P|-4+1×4≤4k-1;其余成立e(P,M)≤ |P|-4+1+2+1+1≤4k。均矛盾。若|A∩M|=1,由对称性仅需讨论a∈M;g∈M;b∈M即可。前两种有e(P,M)≤|P|-5+1×3+2×2≤4k+1和e(M,P)≥2(|M|-1)+3≥ 4k+3,矛盾。其余成立e(P,M)≤|P|-5+ 1×4+5≤4k和e(M,P)≥2(|M|-1)+3≥ 4k+3,矛盾。
② 若两条边交于1点,可以记e1=ab,e2=bc,e3=fg,e4=gh。令A={a,b,c,f,g,h},则A⊆M不成立。否则e(P,M)≤|P|≤4k-1和e(M,P)≥2(|M|-6)+3×6≥ 4k+8相矛盾,A⊆P也不成立。否则,对任意v∈V(G0),必有|N[v]∩M|≤2,故|M|≤2×3k/3=2k,矛盾于|M|≥2k+1。
若|A∩M|=5,由对称性仅需讨论a∈P和b∈P。二者均成立e(M,P)≥ (|M|-5) +3×5≥ 4k+7。前者有e(P,M)≤|P|-1+1≤4k-1,后者有e(P,M)≤ |P|-1+2≤4k。均矛盾。若|A∩M|=4,由对称性仅需讨论a,b∈P;a,g∈P;②a,c∈P;③a,f∈P;b,g∈P。均成立e(M,P)≥2(|M|-4)+3×4≥4k+6。且前2种有e(P,M)≤|P|-2+1+2≤4k;后1种有e(P,M)≤ |P|-2+1+1≤4k-1;其余成立e(P,M)≤ |P|-2+2+2≤4k+1。均矛盾。若|A∩M|=3,由对称性仅需讨论a,b,c∈M;a,b,f∈M;a,c,g∈M;a,b,g∈M;a,c,f∈M。这些情况下均成立e(M,P)≥2(|M|-3)+3×3≥ 4k+5。且前3种有e(P,M)≤|P|-3+1+2+1≤4k;后1种有e(P,M)≤ |P|-3+2+2+1≤4k+1;其余成立e(P,M)≤|P|-3+1×3≤4k-1。均矛盾。若|A∩M|=2,由对称性讨论a,b∈M;a,g∈M;b,g∈M;a,c∈M;a,f∈M。这些情况下均成立e(M,P)≥2(|M|-2)+3×2≥ 4k+4。讨论e(P,M):前2种有e(P,M)≤|P|-4+1×3+2≤4k;后2种有e(P,M)≤ |P|-4+2×2+1×2≤4k+1;其余成立e(P,M)≤ |P|-4+1×4≤4k-1。均矛盾。若|A∩M|=1。由对称性仅需讨论a∈M和b∈M。均成立e(M,P)≥2(|M|-1)+3≥4k+3。且前者有e(P,M)≤|P|-5+1×3+2×2≤4k+1,后者有e(P,M)≤ |P|-5+1×4+2≤4k。均矛盾。
情形4若e1,e2,e3,e4有3个交点。
① 4条边依次相连。可以记e1=ab,e2=bc,e3=cd,e4=df。令A={a,b,c,d,f}。则A⊆M不成立。否则e(P,M)≤|P|≤4k-1和e(M,P)≥2(|M|-5)+3×5≥ 4k+7相矛盾。A⊆P也不成立,否则对任意v∈V(G0),必有|N[v]∩M|≤2。故|M|≤2×3k/3=2k,矛盾于|M|≥2k+1。
若|A∩M|=4,由对称性仅需讨论a∈P;b∈P;c∈P即可。均成立e(M,P)≥2(|M|-4)+3×4≥ 4k+6。且前1种有e(P,M)≤|P|-1+1≤4k-1;其余成立e(P,M)≤ |P|-1+2≤4k。均矛盾。若|A∩M|=3,由对称性仅需讨论d,f∈P;c,f∈P;a,f∈P;c,d∈P;b,d∈P。均成立e(M,P)≥2(|M|-3)+3×3≥ 4k+5。且前3种有e(P,M)≤|P|-2+1+2≤4k;后2种有e(P,M)≤|P|-2+2+2≤4k+1;其余成立e(P,M)≤ |P|-2+1+1≤4k-1。均矛盾。若|A∩M|=2。由对称性仅需讨论d,f∈M;c,f∈M;a,d∈M;a,f∈M;c,d∈M;b,d∈M即可。这些情况下均成立e(M,P)≥2(|M|-2)+3×2≥ 4k+4。讨论e(P,M):前3种有e(P,M)≤|P|-3+1+2+2≤4k+1;后2种有e(P,M)≤|P|-3+1+2+1≤4k;其余成立e(P,M)≤ |P|-3+3×2≤4k+2。均矛盾。若|A∩M|=1,由对称性仅需讨论b∈M;c∈M;a∈M。前2种有e(P,M)≤|P|-4+1×2+2×2≤4k+1和e(M,P)≥2(|M|-1)+3≥ 4k+3,矛盾。其余有e(P,M)≤ |P|-4+2×3 +1≤4k+2和e(M,P)≥2(|M|-1)+3≥4k+3,矛盾。
② 若3条边首尾相连,1条边独立。可以记e1=ab,e2=bc,e3=ca,e4=df。记A={a,b,c,d,f}。重复4.1的情形,可得A⊆M和A⊆P均不成立。
若|A∩M|=4,由对称性仅需讨论a∈P;d∈P。均成立e(M,P)≥ 2(|M|-4)+3×4≥ 4k+6且前者成立e(P,M)≤|P|-1+2≤4k;后者成立e(P,M)≤|P|-1+1≤ 4k-1。均矛盾。若|A∩M|=3。由对称性仅需讨论a,b∈P;d,f∈P;a,d∈P。均成立e(M,P)≥2(|M|-3)+3×3≥4k+5。且第1种有e(P,M)≤ |P|-2+2+2≤4k+1;第2种有e(P,M)≤ |P|-2+1+1≤4k-1;其余成立e(P,M)≤ |P|-2+2+1≤4k。均矛盾。若|A∩M|=2,由对称性仅需讨论a,b∈M;d,f∈M;a,d∈M。均成立e(M,P)≥ 2(|M|-2) +3×2≥4k+4。且第1种有e(P,M)≤|P|-3+1+1+2≤4k;第2种有e(P,M)≤ |P|-3+2×3≤4k+2;其余成立e(P,M)≤ |P|-3+2+2+1≤4k+1。均矛盾。若|A∩M|=1,由对称性仅需讨论a∈M;d∈M。前者成立e(P,M)≤ |P|-4+2×2+1×2≤4k+1和e(M,P)≥2(|M|-1)+3≥ 4k+3,矛盾。后者成立e(P,M)≤ |P|-4+1+2×3≤4k+2和e(M,P)≥2(|M|-1)+3≥ 4k+3,矛盾。
情形5若e1,e2,e3,e4有4个交点,则可以记e1=xy,e2=yz,e3=zt,e4=tx。记A={x,y,z,t}。则A⊆M不成立。否则e(P,M)≤|P|≤4k-1和e(M,P)≥2(|M|-4)+3×4≥ 4k+6相矛盾。A⊆P也不成立,否则对任意v∈V(G0),必有|N[v]∩M|≤2。故|M|≤2×3k/3=2k,矛盾于|M|≥2k+1。
若|A∩M|=3,由对称性可知,仅需讨论x,y,z∈M且t∈P。则e(M,P)≥2(|M|-3)+3×3≥ 4k+5,e(P,M)≤|P|-1+2≤4k。矛盾。若|A∩M|=2。由对称性知,仅需讨论x,y∈M;x,t∈M。均成立e(M,P)≥2(|M|-2)+3×2≥ 4k+4和e(P,M)≤|P|-2+2+2≤4k+1。矛盾。若|A∩M|=1,由对称性仅需讨论x∈M。此时,e(P,M)≤|P|-3+2×3≤4k+2,e(M,P)≥ 2(|M|-1)+3≥ 4k+3。矛盾。
综上所示,假设不成立。故结论成立。
综上,本文可以得到以下Cn×P2的符号全加强数的结论:


