矩形阈值函数神经场方程解的存在性与稳定性

禹磊，秦子雁，唐白雪，金德泉

(广西大学数学与信息科学院， 广西南宁530004)

0 引言

Amari 动力神经场最早由日本神经网络专家甘利俊一于20世纪70年代末提出，用于在大尺度上描述神经元活动规律。该模型不同于传统神经网络模型，它不关注微观的个体神经元活性变化情况，而是从宏观的角度整体上考虑神经活性分布，其结果更符合于目前fMRI等技术手段所获得的人脑活性分布的特点，能够更好地描述人在认知行为中脑区的活动，并能够较好说明工作记忆和短期记忆等在内的记忆现象，解释一些复杂的认知现象。

在Amari动力神经场模型中，对动力神经场性质起到决定性作用的部分是该模型的阈值函数和相互作用核[1-2]。在大部分研究中，阈值函数一般选择为传统的阶跃函数或Sigmoid型函数。这一类函数更接近神经元的激活函数，具有较好的神经生理学背景。但在实际应用中，这一类阈值函数主要描述兴奋型神经元的作用，没有考虑抑制性神经元的作用,这就造成了动力神经场的层向抑制作用只能通过正活性神经元依据相互作用核对其邻域内的神经元产生，与实际中抑制型神经元也能产生层向相互作用的情况并不十分符合。本文主要在n维欧氏空间Rn中，讨论当阈值函数为矩形函数，相互作用核为DoG (differential of guassin function)函数时[3-4]，Amari动力神经场方程静态解的存在性和稳定性[5]。Amari动力神经场方程是一个典型的非线性微分积分方程[6]，具有复杂的动力学性质，在高维空间中的情况更为复杂[7-8]，一直是该领域研究的热点[9-10]。对于其动力学性质的研究，可以为动力神经场在认知科学和机器学习等领域，如图像处理、场景分割[11-12]等方面的应用提供理论依据。

1 预备知识

Amari模型为：

(1)

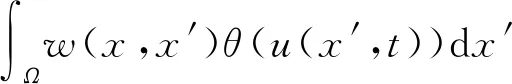
w(x)=Ag(z,σ)-Bg(z,γσ),γ>1，

(2)

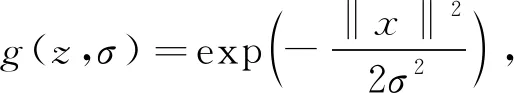
为了能够使得抑制型神经元也产生与兴奋型神经元类似的层向相互作用，同时因为神经元具有激活保护的性质，即神经元对过高的神经活性输入具有保护性低通作用，令θ(u)为矩形函数，即:

在讨论神经场方程的静态解时，一般假定S(x,t)是时不变的，即对所有t≥0，都有S(x,t)=S(x)。令Ω为Rn，此时得到:

(3)

令∂u/∂t=0，所有静态解都满足：

在关于生理心理学，神经心理学，机器械视觉与认知这些神经场的运用中，φ解，∞解，球形解是关注的重点，这些解的定义如下：

定义1当u*(x)≤0,∀x∈Rn,u*(x)称为φ解；当u*(x)>0,∀x∈Rn,u*(x)称为∞解；当u*(x)>0,∀x∈D,并且u*(x)≤0,∀x∈{RnD},其中，D为球形领域，称为球形解。

令wmax(x)=max{0,w(x)}，wmin(x)=min{0,w(x)}，假设相互作用核满足以下条件：

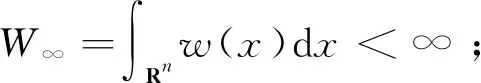
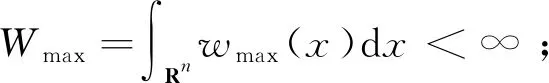
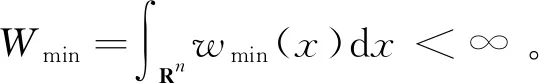
且S(x)有界时，即:

s0≤S(x)≤S0,∀x∈Rn。

(4)

2 主要结果

命题1当w(x)为式(2)所示的DoG函数时,S(x)有界，如式(4)所示, 则:

① 当Wmin+s0+h>0时，系统(3)所有静态解都是∞解；

② 当系统(3)存在∞解，则Wmax+S0+h>0。

证明由于阈值函数θ(u):R→{0,1}，当Wmin+s0+h>0,∀x∈Rn时，有:

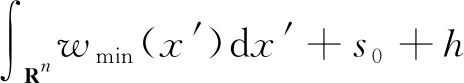
从而所有解都是∞解。

当存在解是∞解,u*(x)>0,∀x∈Rn，有:

=Wmax+S0+h,

即Wmax+S0+h≥u*(x)>0,证毕。

命题2当w(x)满足式(2),S(x)满足式(4),则:

① 当Wmax+S0+h≤0，系统(3)所有静态解都是φ解；

② 若存在φ解u*(x)≤0，则Wmin+s0+h≤0。

证明由于阈值函数θ(u):R→{0,1}，当Wmax+S0+h<0，有:

=Wmax+S0+h<0。

由定义1可得系统(3)的静态解都是φ解。

当存在φ解u*(x)=hφ≤0,∀x∈Rn,有:

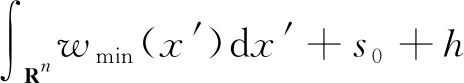
即Wmin+s0+h≤0,证毕。

命题3当w(x)满足式(2),S(x)满足式(4),当系统(3)存在球形解时，有：

①Wmax+S0+h>0;

②Wmin+s0+h≤0。

证明若u*(x)为球形解，当u*(x)>0,∀x∈D时，有：

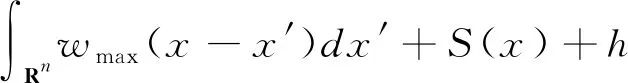
即Wmax+S0+h>0。

当u*(x)≤0,∀x∈{RnD}时，有：

即Wmin+s0+h≤0,证毕。

3 结论

本文讨论了n维欧氏空间Rn中Amari动力神经场方程的动力学性质。在假定阈值函数为矩形函数，相互作用核为DoG函数时，得到了一些关于动力神经场静态解的存在性和稳定性的结论，并对这些静态解的稳定性情况进行了讨论和分析。这些研究成果对于神经场的动力学性质的研究具有较高的理论价值，并可以为动力神经场在认知科学和机器学习等领域的应用提供理论依据。