大学数学考试不及格率估计及其影响因素统计分析

黄敢基，欧诗德，李琼

(1.广西大学数学与信息科学学院， 广西南宁530004；2.玉林师范学院数学与统计学院， 广西玉林537000；3.玉林师范学院物理与电信工程学院， 广西玉林537000)

0 引言

教育部高度重视全面提升本科人才培养质量，本科高校除了要做好一流学科建设外，还要以本科为本，建设一流本科专业。本科高校要充分认识到本科教育是建设高等教育强国的根基，要意识到“本科不牢，地动山摇”。 教师要通过课堂教学改革提升教学质量，树立优良的教风和学风，激发学生的学习兴趣和创新能力[1]。 现在许多本科高校已采取实际行动，通过教学管理和教学模式、方法、课堂、课外学习等方面的改革促进本科教育发展。学生学习成绩是教学评估指标，可作为本科教学质量的代理变量，成绩的提高能体现教育质量的改进[2]。为了制订合理的管理制度，管理者需要了解学生总体对课程的学习情况和评估课程教学效果。因此对学生考试成绩的研究对教学管理者和教师有积极的意义。

关于大学本科生的学习情况研究很受学者关注。例如，文献[3]研究大学数学不及格现象及其影响因素，运用Logistic模型分析学生本科考试不及格与高考成绩、性别、生源地和学生评教关系，发现高考成绩对本科数学考试不及格率有一定影响，但不是影响的主要因素。此外，针对高考成绩与本科考试是否有显著关系问题，文献[4-7]也做了研究。例如文献[5]运用Pearson相关系数统计研究高考数学成绩与大学数学专业课成绩相关性，发现高考数学成绩与大学专业课成绩关系无显著相关性。文献[6]发现高考成绩与大学阶段学习成绩相关度很低。什么因素显著地影响学生的本科考试？如何改进教学管理和教学方式和方法，文献[8-10]做了调查研究与分析。 例如文献[8]对大学数学教学现状进行了调查，发现学生学习大学数学的目的和态度不正确，学习兴趣不大，认为数学对本专业学习作用不大，不需要学习过多的数学知识。

本文从某本科高校的高等数学公共课期末考试成绩中抽取样本，以班为抽样单元抽取6个班，运用抽样技术理论，估计该门公共课不及格率。 比较不同班级不及格率和平均分的内在差异，各班的学习成绩差异，揭示教师的教学水平与学生成绩的关系。此外，为了了解学生的本科期末考试成绩是否显著地受到学习基础影响，抽取期末考试成绩中等以上的学生和期末考试不及格考生样本，建立假设检验，比较这些学生的高考数学成绩，分析这科目高考成绩差异对期末考试成绩影响的显著性，讨论影响本科学习成绩的主要因素。

1 研究方法

1.1 总体比例估计

总体中具有某种特征的个数占总体总数的比例估计。设总体总数为N，设示性变量为：

若抽取了容量是n的样本，则样本均值为：

的置信水平为1-α的置信区间是

1.2 两总体比例差异分析

设两总体X与Y独立，分别从中抽取n1和n2个样本进行观察，发现其中各有m1和m2个具有某种特性。 这两个总体中具有该种特性的比例分别为p1和p2，其估计为：

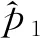
统计量为：

(1)

p1-p2的置信水平为1-α的置信区间为：

(2)

2 统计与讨论

2.1 总体不及格率估计

为了估计某本科院校全校学生对高等数学公共课期末考试不及格率，对该门课程考试情况进行调查。该门课程共有3 162人参加期末考试，全校有25个班选修，期末考试采用同一份试卷和同一评分标准。以班为抽样单元，做整群抽样。随机抽取了6个班，其统计特征见表1。

表1 考试情况Tab.1 Examination results

初级单元平均规模：

该总体不及格人数的比例为：

其估计的方差为：

所以其估计的标准差为：

由式(2)得，不及格率估计的95 %的置信区间为(0.287 307 8，0.509 084 0)。

以上数值结果表明，该门公共课期末考试不及格率估计为39.8 %，估计的标准差为0.056 6，95 %的置信区间为(0.287 307 8，0.509 084 0)。

2.2 不同班级不及格率的差异显著性检验

设不同班级的学生来自不同的总体，不及格率无显著差异。 建立假设：

H0∶p1=p2，H1∶p1≠p2。

选择Z统计量(1)，给定显著水平α=0.05，利用R统计软件编制程序，得到检验结果如表2所示。

表2 不及格率差异Tab.2 Failure rate difference

注1：表中的数据为检验的p值，“*”表明在显著水平为0.05下有显著差异。

表2说明在显著水平0.05下1班与2班不及格率无显著差异，1班、2班与其他班不及格率有显著差异。3班与4班、5班不及格率无显著差异，与6班有显著差异。 4班与5班不及格率无显著差异，与6班有显著差异。5班与6班不及格率有显著差异。 这是不同教师授课的6个班，学生的成绩在一定程度上反映了教师的教学水平。因此，从不及格率的角度看，有些教师的教学水平是有显著差异的。

2.3 学习成绩的影响因素

通过比较各班的平均分来说明教师教学水平因素是否影响学生的考试成绩。有关数据及学生对老师的主观评价见表3。

表3 平均分和教师的评价Tab.3 Average scores and teacher evaluations

建立假设：

H0∶μ1=μ2，H1∶μ1≠μ2，

选取T统计量：

分别从各总体中抽取容量是13的样本，做均值检验，检验的p值见表4。

结果表明，在显著水平为0.05下各班平均分无显著差异。 因此，从平均分角度看，教师的教学水平无显著差异。

表4 平均分差异Tab.4 Average score difference

注1：表中的数据是检验结果的p值。

对抽取的样本再做方差分析，结果如表5。

表5 教学水平因素方差分析Tab.5 Variance analysis of teaching level factors

方差分析结果说明，在0.05的显著水平下，教师的教学水平无显著差异。

学生因素分析。 通常来说，学生之前的学习基础对大学的学习有一定影响，这个因素是否显著地影响了学生期末考试成绩？本文分别从各班不及格的学生和成绩在70分以上的学生中抽取样本，观察他们的期末考试成绩和高考数学成绩。期末考试成绩中上水平的学生记为A组，期考不及格的学生记为B组，对比这些学生高考成绩，假设检验结果见表6。

表6 A组和B组高考成绩对比显著性检验Tab.6 Significance test of college entrance examination achievement between A and B

检验结果表明，在显著水平0.05下，期末考试在70分以上的学生，其高考数学成绩与不及格学生的高考成绩没有显著差异。 这说明高考数学成绩不是影响本科期考试成绩的主要原因。

实际上，个人的学习态度，学习习惯，学习兴趣，学习目的等因素对学习成绩影响很大。为什么一些高考成绩不错的学生到大学后没学好？不妨看看该校学工处对学生的问卷结果(表7)。

表7 调查问卷Tab.7 Questionnaire

由上述调查结果可见很多学生进入大学后学习目的很不明确，没有了学习目的，很难确保良好的学习态度，从而很难顺利通过期末考试。

3 结论

为了解本科生数学考试情况，本文采用抽样技术和统计推断理论和方法对某高校高等数学公共课期末考试进行了研究，抽取了不同教师授课的6个班估计了该门公共课不及格率，并运用假设检验技术，比较不同班级不及格率和平均分的差异。 数值结果表明，在显著水平为0.05下，部分班级不及格率有显著差异，这说明教师的教学水平对不及格率有显著影响。而对该组样本从平均分角度进行比较检验，数值结果表明，教师的教学水平在0.05水平下没有显著差异，这可能是由于部分班级存在学生成绩两极分化严重的原因。 为了了解学生的高考数学成绩是否显著地影响大学数学的考试成绩，从期末考试成绩中等以上的学生和期末考试不及格学生抽取样本，作假设检验，比较这些学生高考数学成绩，分析高考数学成绩对本科期末考试成绩影响的显著性。 数值结果表明，高考数学成绩对本科期末考试成绩没有显著影响。因此，学生考试不及格率不应该怀疑自己已有的基础，也不应该过多抱怨教师的教学水平不够好，更重要的是要明确学习目的，端正学习态度，养成良好的学习习惯。另一方面，大学数学教师需要不断提高教学水平，不断改进教学方式和方法，使课堂学习生动活跃有趣，培养学生的学习兴趣。同时，注意了解学生思想动态，管理好学生的学习纪律，营造良好的学风，切实提高课堂教学效率。