利用试探函数法求Burgers-Huxley方程的精确解

高忠社，彭聪明

（天水师范学院 数学与统计学院,甘肃 天水 741001）

1986年Satsuma首次提出了Burgers-Huxley方程，方程的形式为

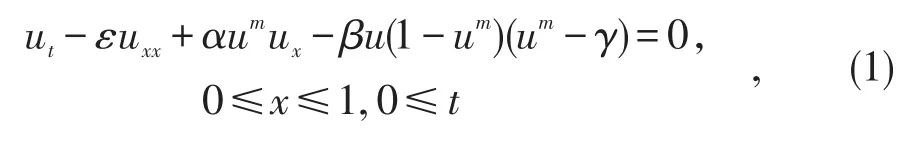
其中 ε,α,β,γ,m 为常数.上述方程为一个重要的非线性反应扩散方程，由于该非线性方程地描述了自然界许多的非线性现象，对于该问题的求解，无论是物理学界还是数学界的科学工作者都十分关注，先后出现了很多方法来求解非线性偏微分方程。如Backlund变换法，Darhoux变换法，Hirota方法，齐次平衡法，双曲函数展开法，辅助函数展开法等，文献[3]中使用试探函数方法讨论了非线性热传导方程的孤立波解，文献[4-7]使用试探函数方法对于不同类型的非线性偏微分方程进行了讨论，文献[8-10]对于Burgers-Huxley方程用数值方法进行了求解，本文将尝试使用试探函数方法对于Burgers-Huxley方程进行求解.

1 试探函数方法

试探函数法是基于Cole-Hopf变换的基本思想，该方法的基本过程来源于Cole-Hopf变换，并选取适当的试探函数，求出相应的偏导数，代入原非线性微分方程，就可将非线性偏微分方程化为一个代数方程组，然后利用待定系数法确定相应的系数，即可得到非线性偏微分方程的解析解．

引入如下试探函数，设

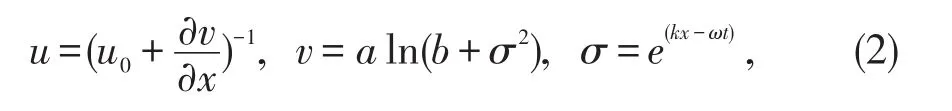
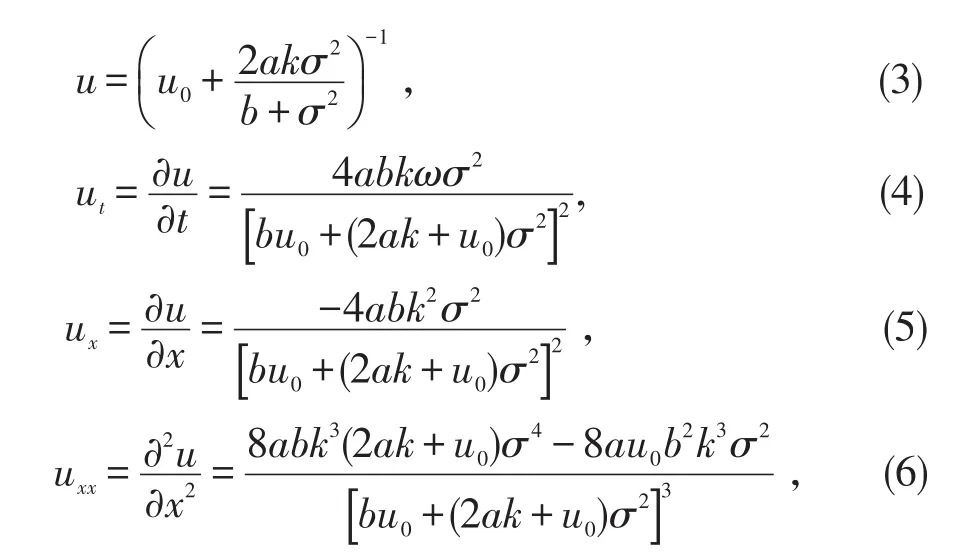
将上述(3)-(6)式代入微分方程(1)可得相应的代数方程组.

2 非线性Burgers-Huxley方程的求解

下面考虑如下Burgers-Huxley方程

其中p,q为常数.

将(3)-(6)式代入(7)可得下列代数方程

为了使得上式(8)对任意的实数σ都成立，必有下列代数方程组成立

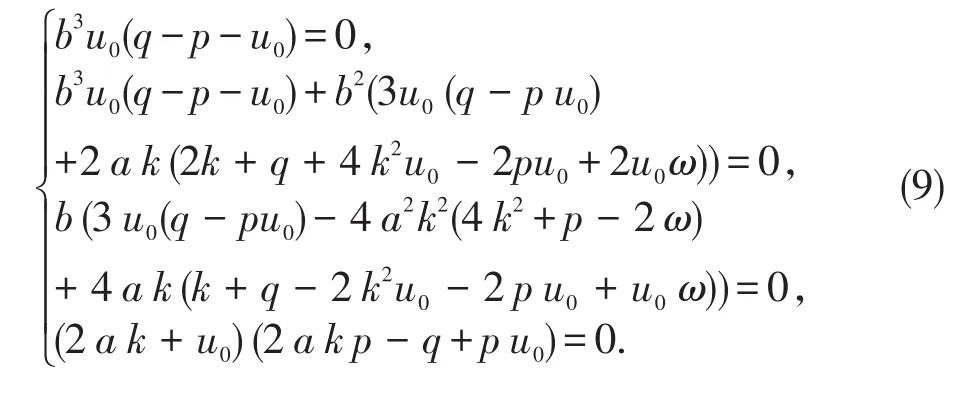
其中b为任意的常数，求解上式(9)得到方程组关于p,q的一组解

先将u0,a,k,ω代入(3)式可得

(11)式为非线性Burgers-Huxley方程的一般形式的行波解，由于b取不同的值，可以得到(7)式多个不同的特解.

下面讨论b取不同的值时，非线性Burgers-Hux⁃ley方程解的情形：

情形1b=1，由(11)式可得该方程的扭状孤波解

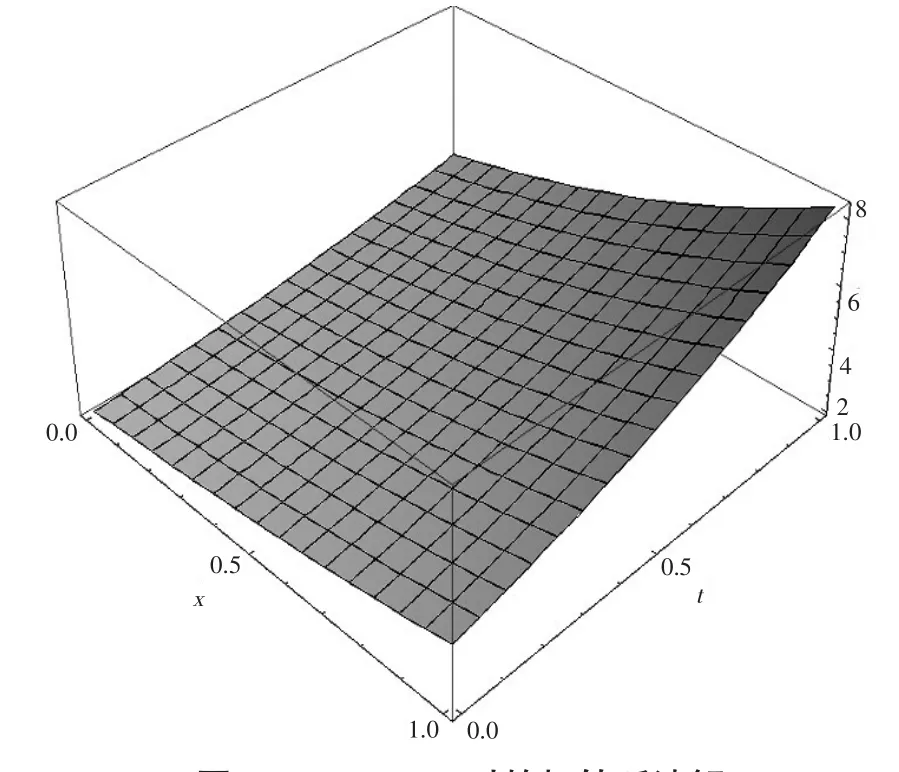
图1 b=1,p=q=1时的扭转孤波解

情形2b=-1，由(11)式可得该方程的奇异行波解

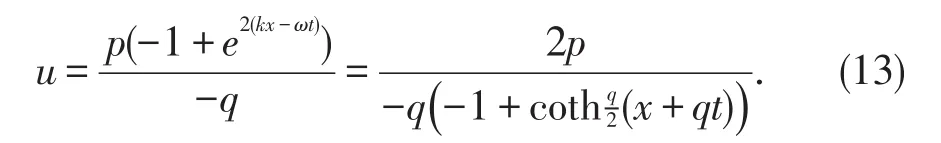
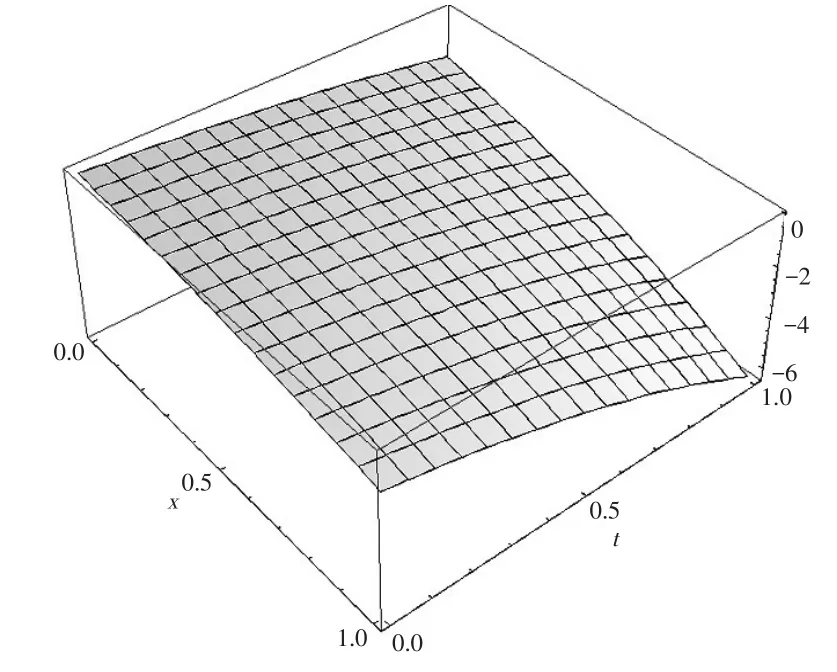
图2 b=-1,p=q=1时的奇异行波解

情形3b=2，由(11)式可得该方程的扭状孤波解

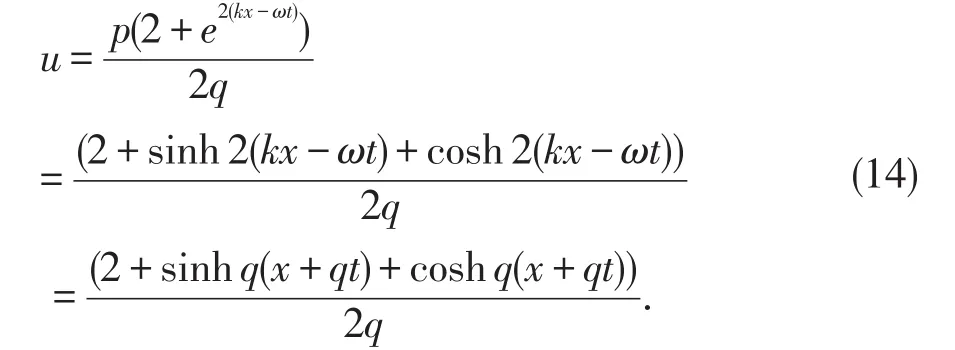
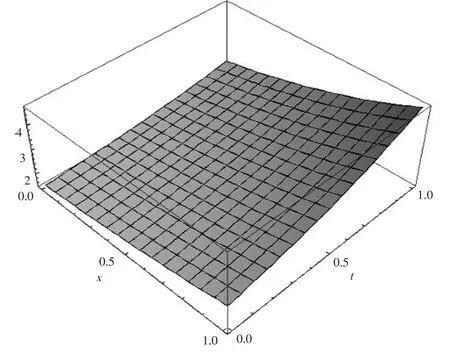
图3 b=2,p=q=1时的扭转孤波解

情形4b=-2，由(11)式可得该方程的扭状孤波解

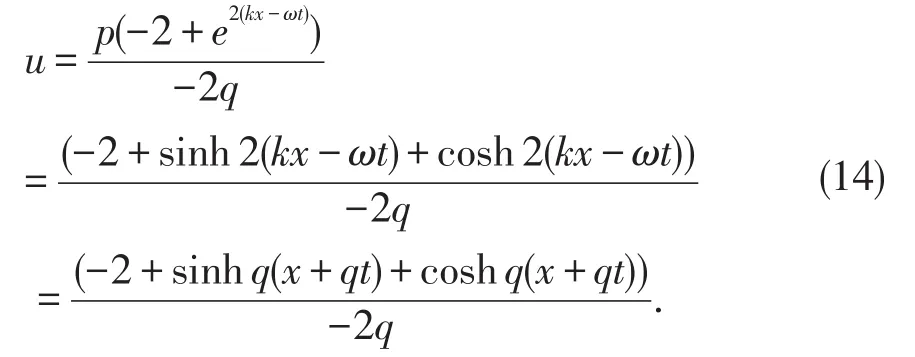
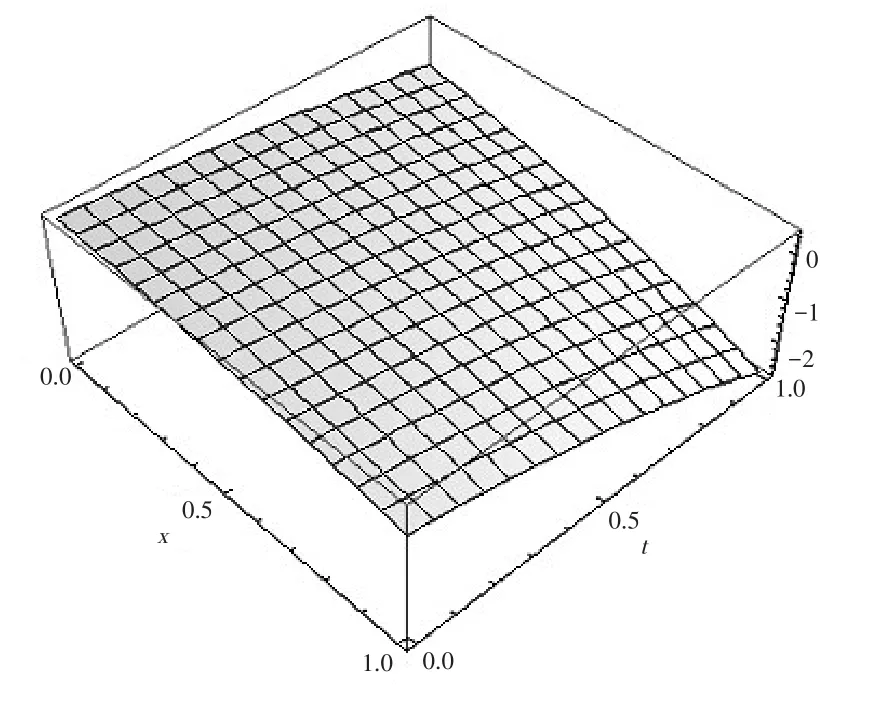
图4 b=-2,p=q=1时的奇异行波解

3 分析讨论

通过引入试探函数的方法，将试探函数的方法应用于非线性Burgers-Huxley方程，由于引入的试探函数比较适合，根据试探函数的方法，将非线性Burgers-Huxley方程的各个偏导数项通过试探函数来表示，其中各个的偏导数项带有参数，再将其代入Burgers-Huxley方程，得到一个关于参数的代数方程组，通过求解代数方程组，确定参数，从而得到Burg⁃ers-Huxley方程的一组行波解，当选取相应的参数以后，可以将行波解转化为扭状孤波解，和奇异行波解，文中只讨论了b=±1，±2时的孤波解，和奇异行波解，对于其他类型可以类似讨论，并使用数学软件Mathematica进行了模拟，得到了不同情形的解的图形.从Burgers-Huxley方程求解过程可以发现，使用试探函数方法求解非线性偏微分方程的时，首要问题是给定相应的试探函数的形式，只要试探函数的形式给定的恰当，该方法求解方程的过程比较直观.该方法也应用于其他类型的非线性偏微分方程.