分数阶Schrödinger方程守恒律的一个注

彭聪明，马草川，高忠社

（天水师范学院 数学与统计学院，甘肃 天水 741001）

1 引言和预备知识

Schrödinger方程是量子力学中的基本方程，近50年来已经被众多数学工作者进行了深入的研究.对于经典Schrödinger方程，人们一般是在称为能量空间的空间中进行研究，更一般的，也可以在空间中进行研究.这种空间的一般性质是它们是基于空间的，而基于空间的优点是线性群在空间中是有界的.经典Schrödinger方程解的适定性问题一般可分为两步来处理，第一步，是对问题所对应的积分方程利用压缩映像原理来证明解的局部存在唯一性.在时间区间上的局部解是积分方程在函数空间中的一个闭球上压缩映像的不动点.基本的工具是著名的Strichartz估计，利用该估计可知当时间取得足够小时，相应的压缩因子可以充分小.第二步，是利用解的先验估计将解的存在时间进行延拓，这些先验估计大都和质量及能量守恒有关.而一般情况下质量守恒及能量守恒的证明都和解的正则性有关，具体来说，一般有两种证法.其一，是基于解对初值的连续依赖性，利用Hj+1解逼近Hj解（其中 j=0,1），使得形式上的计算可以通过逼近序列证明.其二,是基于一个正则化了的方程序列进行逼近，而该正则化了的方程具有形式计算所需要的正则性，最后再通过一个极限过程得到质量守恒和能量守恒.在文献[5]中，Ozawa没有借助逼近过程，直接证明了经典Schrödinger方程解的质量守恒和能量守恒，只用到了算子在Hilbert空间中的自反性.

分数阶非线性Schrödinger方程

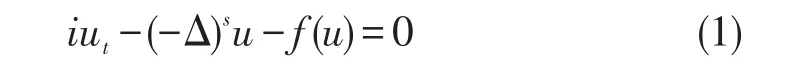
受这些文献的启发，我们利用文献[5]的方法，不借助于解的逼近，直接利用方程解的积分形式证明质量及其能量守恒.

2 主要结果

首先假设非线性项 f(u)满足条件：

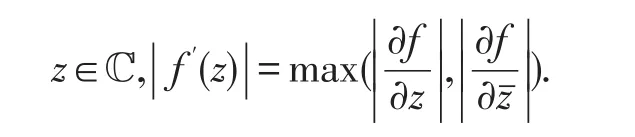
方程(1)所对应的积分形式解，即Duhamel公式为：

定义数对(q,r)称为允许对当且仅当

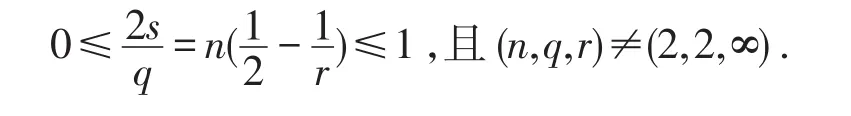
下面我们回顾分数阶Schrödinger方程的Strich⁃artz估计.设，定义Strichartz范数如下

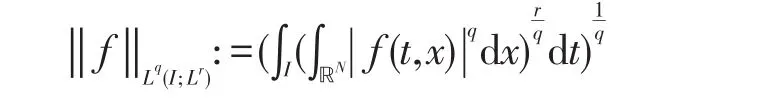
其中(q,r)为允许对.本文中用如下的Strichartz估计：

（1）解的质量及能量守恒.

定理1若 f满足条件1)-3)，设，则对任意，则

证明重写Duhamel公式如下：

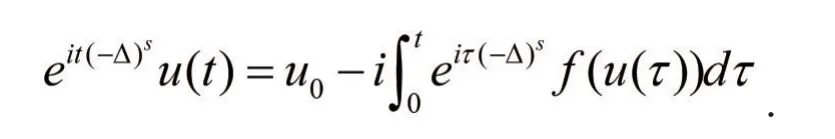
利用自由分数阶Schrödinger算子的性质，我们有

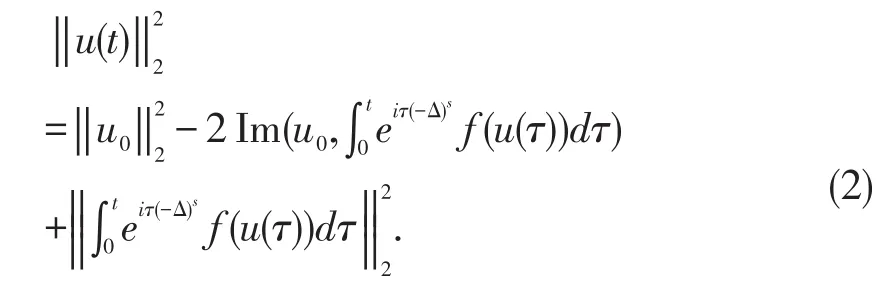
(2)式中间项等于

而最后一项等于

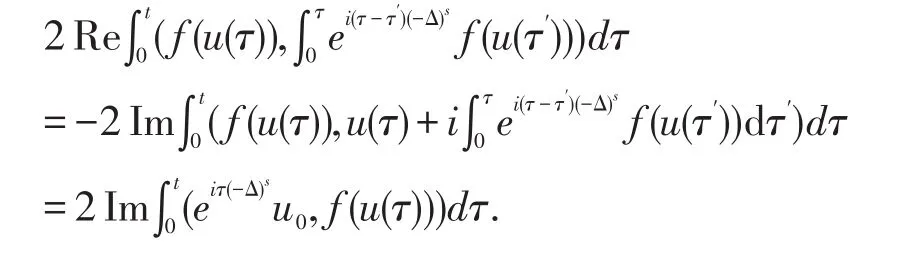
这里用到了非线性项应该满足的条件，故质量中的后两项将会抵消，定理得证.

定理2设 f满足条件1)-3)，为问题的解，其中(q,r)为允许对.则对任意 t∈(-T,T)，则

证明重写Duhamel公式如下：

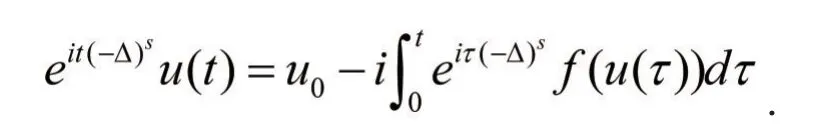
利用自由分数阶Schrödinger算子的性质，我们有

其中(3)式的来源如下：

故定理得证.