基于描述函数法的典型结构非线性识别方法研究

赵中阁，刘杨

（中国航空综合技术研究所，北京 100028）

目前传统的动力学分析中，主要应用的是线性振动理论。在实际工程应用中，其将振动系统线性化后进行数学求解，在大部分情况下都能给出比较满意的结果。正是因为线性振动理论的种种优点，在工程实践中，研究人员总是把所研究的动力学系统尽可能地线性化。在实际的工程环境中，大部分的振动实际上都是非线性的，因而将系统线性化会直接忽略其非线性特性，导致得到的理论结果与实际的振动响应有一定的误差，甚至有时会引发严重的后果[2]。所谓线性振动只是系统在运动较小时的一种近似，并不足以完整描述系统的振动特性。由于对产品动力学环境关注越来越高，特别是在航空航天和兵器等工程领域中的重要性日益突出，线性振动理论和方法已不能满足要求，大量的重要实际问题迫切需要用非线性动力学理论和方法加以研究分析。

有关非线性结构动力学的研究已经进行了相当长的时间，直到 20世纪后半叶，Ibanez[1]和 Masri等[2]。首先提出了关于非线性动力学系统模型的参数识别问题。由于不同的非线性系统具有各自的特性，所以非线性的识别方法也是多种多样的。总体来说，可分为两类，即时域法和频域法。直接提取动力学系统随时间响应的方法称为时域法，将时域数据进行转化，在频域内进行分析的方法叫频域法。

时域法的识别是对动力学系统随时间的响应进行识别，这类方法的优点在于实验数据易于获取，无需对数据进行过多的后处理。频率法通常是通过频率响应函数或频谱分析对非线性加以识别。目前比较主流的非线性识别方法都是频域法。较早研究频域法作系统识别是通过釆用沃尔特拉和维纳级数（Volterra and Wiener series），由 Schetzen提出[3]。Gifford最先把这个方法应用于非线性识别[4]，而后Storer等人在这方面进行了扩展[5]。Khan等[7]人通过高阶频响函数研究了单自由度系统参数的识别，他们继而研究了关于多自由度动力学系统的参数识别问题[8]。Bendat[9]采用高阶频谱的方法研究了系统识别问题。Roberts等人[10]发展了此频谱识别法。其他较早使用频域法作系统参数识别的还有 Yasuda和他的合作者[13-14]，他们把谐波平衡法应用到参数识别过程中。

基于系统的频响函数以及一阶谐波平衡下描述函数的定义，Omer Tanrikulu提出了描述函数法（Describing Functions）识别非线性的方法[15]。Mehmet Bulent Özer在此基础上提出了确定非线性位置的方法，并提出使用Sherman-Morrison求逆法近似求解描述函数的方法[16]。Arslan和 Aykan提出了计算非线性频响函数的方法[17]，之后 Aykan提出了通过部分激励点的频响函数计算完整频响函数矩阵的方法，以及将描述函数变换回恢复力的计算方法[18]。描述函数法识别非线性计算速度快、精度高，是一种实用有效的结构非线性识别方法。

1 描述函数法识别非线性

1.1 原理

谐波激励下的多自由度非线性系统的运动方程可写为：

式中： [M]、[C]、[K]分别为线性系统的质量、阻尼和刚度矩阵；{f}为系统外部激励力（向量）；{x}为系统响应位移（向量）；{N( x,x˙)}为系统的非线性力，其根据非线性的类型表征为位移或速度的函数。

对于谐波激励{f} = {F }eiωt，系统的响应也为谐波{x} = { X }eiωt。由于系统的响应为谐波，则非线性力也为谐波，其可写成：

式中：[Δ(x, x˙)]为与响应相关的“非线性特性矩阵”，其由表征非线性力的描述函数组成[16]：

式中：v为非线性描述函数，其为激励幅值的函数。根据非线性类型不同，具有不同的函数表达形式，且目前主要的无记忆非线性类型的描述函数皆为已知。

从方程(1)可以得到：

非线性频率响应函数（FRF）为：

与之对应的潜在线性频响函数为：

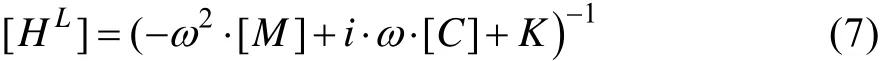
需要注意的是，对于不同的激励量级，由于响应的不同，非线性矩阵一般不同。由此可知，不同激励量级下，非线性频响函数矩阵一般不同。

包含描述函数的非线性矩阵可写为：

其中线性频响函数矩阵[HL]可通过小激励幅值下进行计算近似得到，而非线性频响函数矩阵[HN]却十分难以计算，得到完整准确的非线性频响矩阵所需工作量过大。因此这里对方程(11)进行变形，使得可以通过非线性频响函数矩阵的一列来计算描述函数。

方程(8)两边右乘[HN]有：

式中：

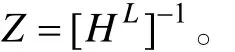
取方程(9)的第i列可以得到：

取方程(10)的第r行可以得到：

则用于非线性位置识别的“非线性指标（NLN）”可写为[16]：

方程(12)中，若在r自由度存在着非线性，则其[Δr]不为0，则NLNr亦不为0，其表明第r自由度存在非线性。NLNr可以通过方程(11)的右边计算得到：

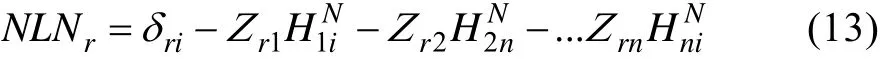
其中，线性频率响应函数已知。非线性频响函数的第i列可以通过仅对多自由度系统的第i自由度进行激励测量全部自由度响应的方法得到。 NLNr为频率依赖，所以可以将计算的所有频率的 NLNr求和来识别非线性位置。

在通过NLN对非线性位置识别后，由于方程(11)中仅存未知量为[Δr]，而在非线性位置已知的情况下，该矩阵的非0元素位置已知，且均可用描述函数表示。即可通过方程（11）计算出不同频率下的描述函数，进而拟合出非线性描述函数在不同位移下的图形，然后通过曲线拟合识别出非线性的类型和参数，以实现对结构非线性的完全识别。

1.2 优点

所有非线性识别方法的共同点是它们都试图去探测、定位和识别非线性。非线性的强弱决定了不同方法的适用性。然而，非线性的级别是很难定义的，并且无法确定是否有一种方法能适用于所有情况的非线性。

目前在工程实际中进行非线性识别时，普遍需要讨论的是两个方面：激励类型和先验数据。激励类型可应用于非线性模态试验。目前普遍用于非线性系统识别的激励类型为步进正弦、正弦扫频和随机三种。其中步进正弦长试验时间的要求通常无法满足工业的需求[21-22]。随机振动试验的主要障碍是其不受控制的本质，全随机信号有些情况下甚至无法成功激发出系统的非线性[24]。正弦扫频试验将扫频试验的速率和正弦试验可控制的本质结合起来，保证了高速和可控性[23]。而描述函数法识别非线性正是适用正弦扫频激励，即其工程可行性较高。

除了激励类型外，现有的非线性识别方法的另一个特点是通常都需要一定数量的先验数据。大多数可用的方法需要系统的一些已知数据，一些方法需要全部或部分质量、刚度和阻尼值[25]，而一些方法需要所分析结构的线性频率响应函数（FRF）以及非线性的类型[26-27]。与上述方法相比，描述函数法识别非线性对先验数据的需求程度较低，仅需要结构的线性FRF即可对非线性完成识别。

在当前的非线性研究领域，描述函数法由于有着上述的优点使得其工程可实现性较高，有着很大的研究价值。

2 案例分析

非线性系统包括单自由度系统和多自由度系统两种。非线性单元的位置包括在自由度与地之间和在两个自由度之间两种。笔者对常见非线性分别进行了单自由度系统非线性位于该自由度与地之间、多自由度非线性在某两个自由度之间、多自由度系统包含多种非线性并位于不同位置的仿真，通过仿真结果验证了描述函数法识别非线性的能力。

2.1 单自由度系统

某单自由度系统，线性系统的数值参数为：m=1 kg，c=1.25 N·s/m，k=500 N/m。由于单自由度非线性系统的非线性单元一定位于该自由度和地之间，所以对于单自由度系统，位置辨识没有意义，可以直接进行类型和参数的识别。

通过 Matlab使用滤波器法求得系统的时域强迫响应[20]。仿真的输入是步进为0.05 Hz的正弦信号，其频率范围为3～8 Hz，输入的正弦信号中混有Matlab生成的均值为 0、标准差为输入信号最大幅值 5%的正态分布的随机信号作为噪声。

非线性系统中的非线性单元类型为符号二次刚度，其描述函数为，其中，p（p=2.3×103）为非线性参数。

通过Matlab仿真，激励信号分别为10、0.1 N，将激励为0.1 N时的频响函数作为线性频响函数，可以得到该单自由度系统的频响函数和不同响应位移下的描述函数如图1所示。对得到的描述函数进行曲线拟合，可以得到该描述函数类型为v=，参数 p=2286。由此可以看出，描述函数法对于单自由度非线性系统的类型识别准确，参数识别精度较高。

图1 符号二次刚度非线性的单自由度系统的频响函数和描述函数

2.2 多自由度系统

与单自由度系统相比，多自由度非线性系统的情况更为复杂。多自由度系统通常可以分为非线性单元仅在两个自由度之间（存在一种或多种）或多种非线性单元分别存在于不同自由度之间的情况。

对于第一种情况，多自由度系统如图2所示，非线性仅位于自由度1和自由度2之间，此时自由度3和4之间没有非线性（k3′4不存在）。对于第二种情况，如图2表示（k3′4存在），此时两种非线性分别位于自由度1和2之间以及自由度3和4之间。多自由度线性 系 统 的 数 值 参 数 为 ： k1= k2= k3= k4= k5=1000 N/m，c1= c2= c3= c4= c5= 5 N·s/m，m1=1 kg, m2=3 kg, m3=4 kg, m4=5 kg

图2 含有非线性的多自由度系统

通过 Matlab使用滤波器法求得系统的时域强迫响应。仿真的输入是步进为0.05 Hz的正弦信号，其频率范围为1～8 Hz，输入的正弦信号中，混有Matlab生成的均值为 0、标准差为输入信号最大幅值 5%的正态分布的随机信号作为噪声。

2.1.1 多自由度系统非线性位于不同自由度之间

此多自由度系统自由度1和自由度2之间的非线性单元为间隙-饱和特性。间隙-饱和是一种混合非线性，其在同一位置包含间隙和饱和两种非线性，其中间隙为0.01 m，线性刚度为500 N/m，饱和值为5 N（饱和位移s=0.2 m）。

通过Matlab仿真，激励信号分别为10、0.1 N。将激励为0.1 N时的频响函数作为线性频响函数，可以得到该多自由度系统的频响函数如图3所示，计算得到的非线性指标如图4a所示。由此可知，非线性位于自由度1和2之间，得到不同响应位移下的描述函数如图4b所示。通过描述函数图形即可判断非线性类型为间隙-饱和，对该类型非线性描述函数

图3 间隙-饱和非线性的多自由度系统频响函数

进行曲线拟合，可知参数：a=0.0099 m，k=469.7 N/m，s=0.0210 m。由此可以看出，对于简单的多自由度非线性系统，描述函数法识别非线性单元的位置准确快速，类型正确，参数具有一定精度。

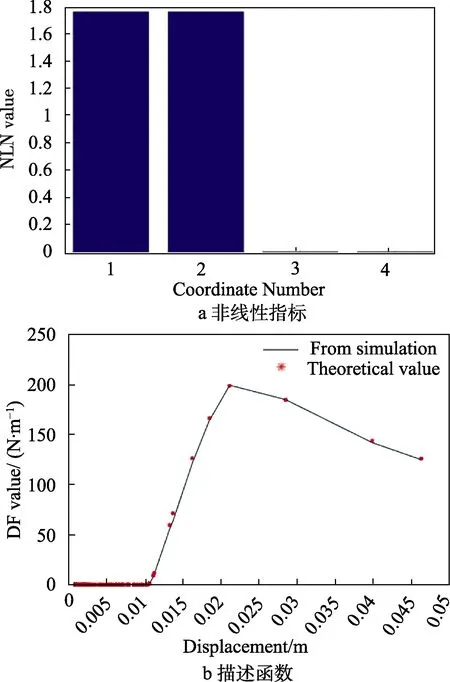
图4 间隙-饱和非线性的多自由度系统非线性指标和描述函数

2.1.2 多自由度系统多种非线性位于不同位置

此系统包含两个非线性单元，分别为三次刚度和间隙特性。其中间隙位于自由度1和2之间，间隙为0.01 m，线性刚度为100 N/m；三次刚度位于自由度3和4之间，非线性参数为1.7×106。

通过Matlab仿真，激励信号分别为10、0.1 N。将激励为0.1N时的频响函数作为线性频响函数，可以得到该多自由度系统的频响函数如图5a所示，计算得到的非线性指标如图5b所示。由此可知，该系统包含两个非线性单元，一种位于自由度1和2之间，另一种位于自由度3和4之间。得到的不同响应位移下的自由度1,2之间和自由度3,4之间的非线性的描述函数如图 6所示，可以看出，自由度 1,2之间的非线性类型为间隙，其非线性描述函数为

读图可得参数 a=0.0100 m，曲线拟合可以得到参数k=99.94 N/m；对自由度3,4之间的描述函数进行曲线拟合，可以得到自由度3和4之间的非线性描述函数为，参数p=1.774×106N/m3。由此可以看出，对于相对复杂的多自由度非线性系统，描述函数法识别的非线性单元的位置准确快速，类型正确，参数精度较高。

图5 三次刚度和间隙非线性位于不同位置的多自由度系统的频响函数和非线性指标

图6 三次刚度和间隙非线性位于不同位置的多自由度系统的非线性描述函数

3 结论

1）文中介绍了描述函数方法识别非线性的原理，并在此基础上，给出了基于频响函数矩阵的某一列计算描述函数的方法，简化了描述函数的计算过程。

2）通过Matlab仿真验证了描述函数识别非线性方法的有效性。

3）相较于其他非线性识别方法，应用描述函数法进行非线性识别计算速度快，对非线性位置和类型识别直观准确，非线性参数识别精度较高，适宜应用于工程实践。