关注几何函数,拓展问题模型
陈丽琴
[摘 要] 函数与几何压轴题是中考数学的重点题型,一般以压轴题的形式出现,该类问题的突破需要融合众多基础知识,采用适当的方法策略.文章对一道中考函数压轴题开展思路突破,拓展解题模型,并提出相应的教学建议.
[关键词] 函数;面积;几何;模型;思想方法
真题呈现
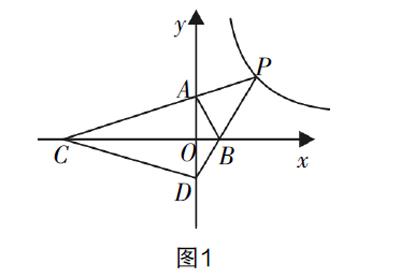
(2019年江苏省徐州市中考数学卷第28题)如图1所示,在平面直角坐标中,O为原点,点A和B分别在x轴、y轴的正半轴上,△AOB的两条外角平分线交于点P,P在反比例函数y= 的图像上.PA的延长线交x轴于点C,PB的延长线交y轴于点D,连接CD,回答下列问题:
(1)求∠P的度数及点P的坐标;
(2)求△OCD的面积;
(3)△AOB的面积是否存在最大值?若存在,请求出最大面积;若不存在,请说明理由.
思路突破
上述属于与几何相关的函数综合题,其中涉及反比例函数、角平分线、三角形性质和几何面积等知识,下面对其突破思路进行探索.
第一步:几何性质利用,突破点P特性
该问求角的度数和曲线上点的坐标,属于较为基础的问题. ∠P是由三角形的两个外角的角平分线相交形成的,因此只需要利用角平分线的性质及三角形外角和知识即可.
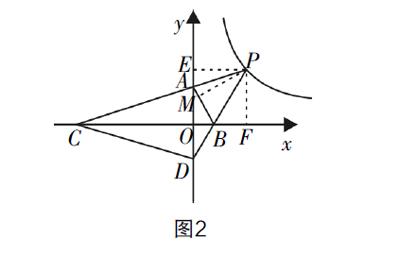
过点P作y轴的垂线,垂足为点E,再过点P作x轴的垂线,垂足为点F,过点P作AB上的垂线,垂足为点M,如图2. 根据角平分线的性质可知,∠PAM= ∠EAM,∠PBM= ∠FBM,则∠PAM+∠PBM= (∠EAM+∠FBM),由三角形的外角和可知∠EAM+∠FBM+∠AOC=360°,其中∠AOC=90°,则∠EAM+∠FBM=270°,∠PAM+∠PBM=135°,所以∠P=180°-135°=45°.
求点P的坐标,由于点P位于函数曲线上,因此只需要求得横坐标或纵坐标其中的一个即可.根据角平分线的性质可得PE=PM=PF,因此可将点P的坐标设为(m,m),代入反比例函数解析式可得m2=9,由于点P位于第一象限,则m>0,解得m=3,所以点P(3,3).
第二步:勾股相似合用,突破三角面积
该问求△OCD的面积,由于该三角形是由PA和PB的延长线以及坐标轴相交形成的,故△OCD为直角三角形,由面积公式可知只需要求得线段OC和OD的长即可.设点A(0,a),B(b,0),由△PEA≌△PMA,△PMB≌△PFB可得AM=AE,BM=BF,于是AB=AM+BM=AE+BF=6-a-b,在Rt△ABO中,由勾股定理可得AB2=OA2+OB2,代入后可解得b= .
分析可证△PEA∽△COA,△PBF∽△DBO,由相似三角形性质可得 = , = ,代入化简可得OC= ,OD= ,所以S△OCD= OC·OD= · · =9.
第三步:不等式性质借用,突破面积最值
该问分析△AOB是否存在最大面积,属于面积存在性问题,由OA+OB+AB=a+b+6-a-b=6可知a+b+ =6,所以2 + ≤6,解得 ≤3(2- ),所以ab≤54-36 ,所以S△AOB= ab≤27-18 ,最大面积为27-18 .
评析 本题目属于函数与几何相结合的综合题,求解时利用到了反比例函数知识、矩形和正方形的性质、全等三角形判定及性质、相似三角形的判定及性质、勾股定理等知识,几何与函数内容结合紧密,主要考查学生的知识应用和逻辑推理能力.问题的核心是第(2)和第(3)问的几何面积分析,相对而言面积模型的构建过程较为简单,难度主要集中在代换运算上,解析时巧妙利用几何性质实现了参数的代换和简化.
模型拓展
上述考题的后两问属于以函数曲线为背景的几何面积问题,其特殊之处在于所涉三角形依托两个坐标轴而构建,且为直角三角形,因此在构建面积模型时可以结合坐标上的点,利用面积公式直接获得. 实际上,求函数中的几何面积属于一类较为典型的问题,根据函数曲线不同、三角形的形状以及所知点坐标不同,其模型的构建过程也大不相同,下面对函数曲线背景下的三角形面积模型的构建方式进行拓展探究.
1. 巧用函数性质,直接构建模型
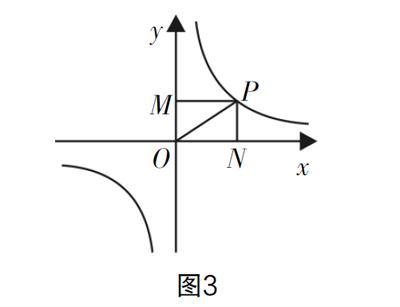
该方式指的是利用函数的几何性质,建立三角形的面积模型,适用于反比例函数背景下的几何面积问题. 如图3所示,设反比例函数的解析式为y= ,根据其性质特征可知常数k可表示为两个变量y和x的乘积,即k=xy,实际上对于该式存在一定的几何意义. 过曲线上任意一点P,分别作x轴和y轴的垂线,垂足分别为点M和N,如图3,连接OP,则k表示的就是矩形PMON的面积,即S矩形PMON=PM·PN=y ·x =k,而S△OPM=S△OPN= k.因此对于三角形的两个顶点分别为原点和反比例函数曲线上的点,以及一条边与坐标轴相重合的三角形,其面积可以表示为 k.
例1:点M为x轴正半轴上的任意一点,过点M作与y轴相平行的直线,与函数y= (x>0)和y= (x>0)的图像分别相交于点P和Q,如图4所示,连接OP和OQ,试求△OPQ的面积.
解析 x轴将△OPQ分割成兩部分,所以其面积可以表示为S△OPQ=S△OPM+S△OQM,而结合反比例函数的几何性质可得S△OPM= k1,S△OQM= k2,即S△OPQ= (k1+k2).
2. 巧作面积割补,构建“铅垂高—水平宽”模型
在函数背景中经常出现求一般三角形的面积问题,此时就无法直接利用面积公式来直接构建求解模型,实际上我们可以通过面积割补的方式借用“铅垂高—水平宽”模型,如图5所示,分别过△ABC的三个顶点作三条与水平方向垂直的垂线,则外侧两条垂线之间的距离称之为“水平宽”,记为a;而穿过三角形内部的直线长度称之为“铅垂高”,记为h,则S△ABC= ah.
证明过程如下 穿过三角形的垂线将△ABC分割为△ADB和△ADC两部分,则△ADB和△ADC可以视为是有共同底AD和不同顶点的三角形,即同底三角形. 设AD分别到点B和点C的距离为h1和h2,则S△ABC= S△ADB+S△ADC= a(h1+h2)= ah. 而在函数背景下使用该模型时就可以结合点的坐标来表示a和h,即a=xC-xB,h=yA-yD,则S△ABC= ·xC-xB·yA-yD,因此解析时只需要分析直角坐标系中关键点的坐标即可.
例2:如图6所示,在平面直角坐标系中,已知点A(-1,-1),B(3,-3),若抛物线经过A,B,O三点,连接OA,OB,AB,线段AB交y轴于点C,试回答下列问题:
(1)求抛物线的解析式.
(2)若点P是线段OB上的一个动点,直线PC与抛物线相交于点D和E,其中点D位于y轴的右侧,连接OD和BD.
①分析△OPC为等腰三角形时点P的坐标;
②试求△BOD面积的最大值以及此时点D的坐标.
解析 这里只分析第(2)问的第②小问,可求得抛物线的解析式y=- x2+ x,过点D作y轴的平行线,与OB相交于点Q,过点B作x轴的垂线,垂足为点H,则△BOD的“铅垂高”为DQ,“水平宽”为OH,所以S△BOD= DQ·OH. 设Q(x,-x),则Dx,- x2+ x,QD= - x2+ x,OH=3,所以S△BOD= ×- x2+ x×3=- x- 2+ ,分析可知x= ,S△BOD取得最大值 ,此时点D的坐标为 ,- .
教学思考
1. 聚焦问题重点,强化基础知識
上述属于中考常见的函数与几何图形相结合的考题,从问题突破的过程来看,充分把握问题重点,灵活使用性质定理是关键. 例如上述第(3)问分析面积最大值时,把握了构建面积模型、转化线段参数的解析重点,充分利用三角形的面积公式和基本不等式的性质等知识来加以突破. 因此在开展考题教学时,需要教师首先引导学生对问题结构进行拆解,挖掘问题实质,然后结合所涉内容来思考问题突破所需的定理定义、公式方法等,并进行系统的整理,帮助学生完成知识的强化.
2. 关注思路构建,拓展解题思维
函数背景中的几何面积问题是初中数学的代表性问题,因融合了几何与函数相关知识,具有极高的综合性,因此在问题突破时特别需要关注思路的构建过程,包括构建模型,转化策略,解析方法等. 例如上述在分析几何面积时由面积公式出发,将问题转化为代数问题,利用基本不等式的性质来分析最值. 另外在教学时还需要教师引导学生探究类型问题的突破策略,总结模型构建的方法,逐步提升学生的解题思维.
3. 渗透思想方法,提升综合素养
考题突破的过程中需要使用对应的思想方法来指导问题转化. 例如上述在分析面积问题时涉及了模型思想、化归转化思想和数形结合思想,这也是函数与几何综合题常用到的数学思想. 因此教学时需要教师适度渗透数学思想,合理引导思考,让学生经历思想方法指导解题的过程,在解题中逐步感知数学思想. 考题教学的最终目标是提升学生的综合素养,而渗透了数学思想的问题探究能够全方面地提高学生的素质,值得倡导.

