利用典型模型 提升核心素养——剖析一道典型解析几何题的错解

高中学生学习解析几何过程中一定会遇到这类题：被抛物线所截长为3的线段的中点到轴的距离的最小值为多少？这道题有些学生是这样解的，过程如下(如图所示)：

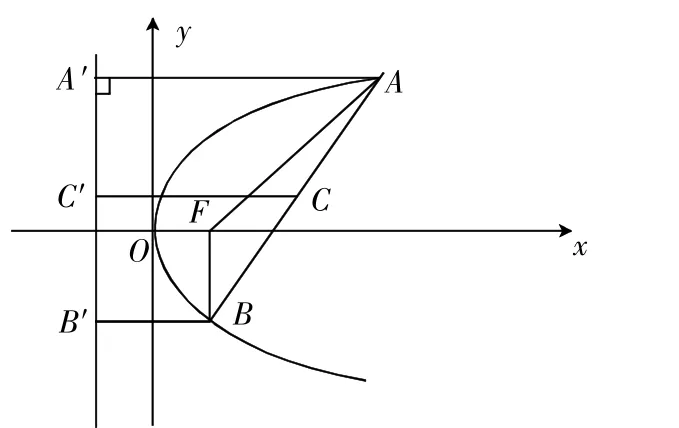
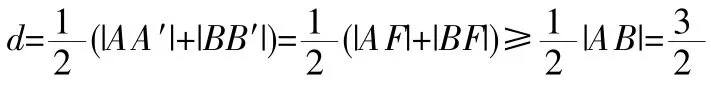
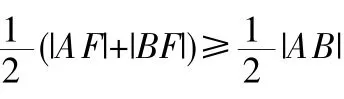
那么如何模型这类题呢？可见，这类题借助图形和简单的平面解析几何知识是不够的，必须从数的角度，建立合适的数学模型，进行严谨的逻辑推理和数学运算来解决问题。

下面从数的角度建立不同的函数与方程模型，借助函数与方程知识进行解决：(设|AB|=a)

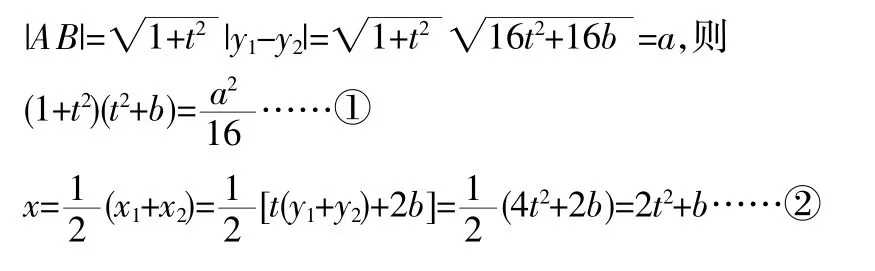
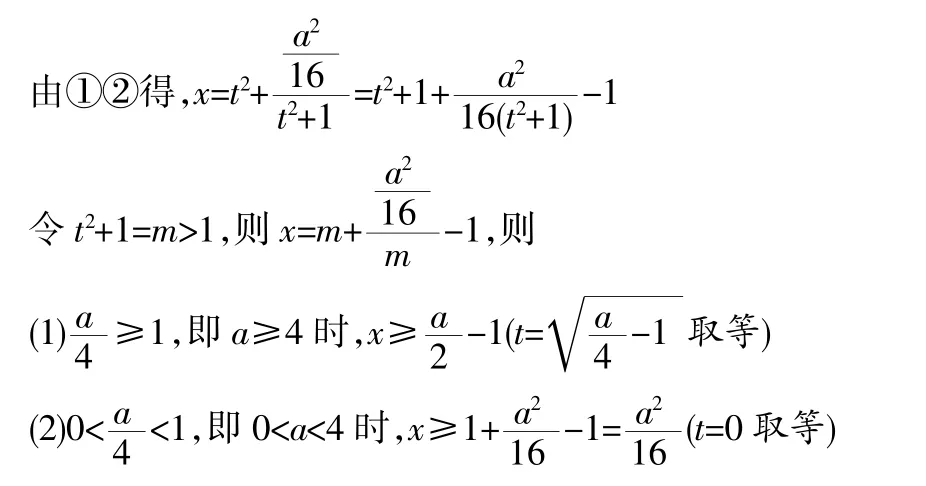
模型二：设中点 C(x0，y0)，设 A(x1，y1)，B(x2，y2)，直线的倾斜角为 α

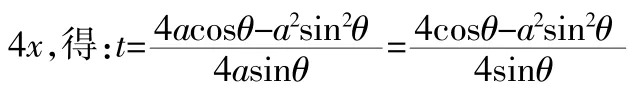
模型四：设 A(t12，2t1)，B(t22，2t2)，C(x，y)

分析点评：

1.上述前三种模型方法的不同之处在于对弦长|AB|的处理不同，模型一是最常规的弦长处理方式，最后将x的最值转化为关于t的函数最值，模型二、三则打破常规，变向使用弦长和点在曲线上，最后转化为关于倾角的三角函数的最值问题。引入参数的方式不一样，得到的代数形式也不一样，但归宿相同，这充分体现了代数本质的一致性和灵活性。

2.模型四与前三种模型的思路不同，不是正面求解，而是先求中点的轨迹方程，再用方程限制范围，此解法充分体现了函数、方程、不等式在解析几何中的应用。

3.由上述模型可得出此类题的一般结论：设抛物线方程为y2=2px(p＞0)，弦长|AB|=a，则AB中点C 到 y轴距离最小值dmin；

解析几何是用代数方法研究几何问题的数学分支，其中的题目可涉及到函数、三角、不等式等各种数学知识，这就决定了一个解析几何问题可能有多种不同的解法。解析几何的一题多解可以提高思维的灵活性，拓展学生的思路，进而可以提高解决数学综合问题的能力，从而提升学生的核心素养。