归纳演绎拓思路，怎样解题求自然——由阿基米德折弦定理说开去

☉浙江省台州市三门初级中学 李如军

让学生学会解题，更要让学生追寻试题的源头，学会自己编题才能提升解题境界.笔者有幸得知2018年台州市中考第24题源自阿基米德折弦定理，遂对该定理和中考题做了一番研究与整理，以飨读者.

一、定理呈现

1.阿基米德折弦定理

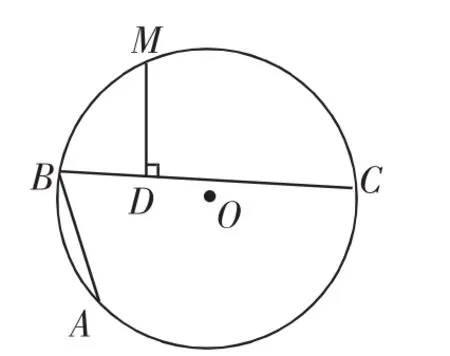
图1

图2

2.解法欣赏

（1）补短法.

解法1：如图2，延长DB至F，使BF=BA，连接AC.

由M、B、A、C、四点共圆，得∠1+∠MBA=180°.

又∠3+∠MBF=180°，则∠MBA=∠MBF.

又MB=MB，BF=BA，则△MBF △MBA.

则∠F=∠MAB=∠MCB，则MF=MC.

又MD⊥CF，则CD=DF=DB+BF=AB+BD.

解法2：如图3，延长CD至F，使FD=CD.

由BM为圆O的弦，得∠3=∠4=∠5.

则∠1-∠5=∠2-∠4.

图3

则BF=AB.

则CD=AB+BD.

解法3：如图4，作MH⊥射线AB，垂足为H.

由M是弧ABC的中点，得MA=MC.

由MD⊥BC，得∠MDC=90°=∠H.

又∠MAB=∠MCB，则△MHA △MDC.

则AH=CD，MH=MD.

又MB=MB，则Rt△MHBRt△MDB.

则HB=BD.

则CD=AH=AB+BH=AB+BD.

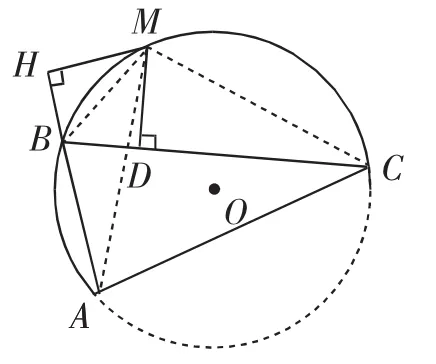
图4

图5

（2）截长法.

解法4：如图5，在CD上截取DG=DB.

由MD⊥BG，得MB=MG，∠MGB=∠MBC=∠MAC.

即∠MGB=∠MCB+∠BCA=∠MCB+∠BMA.

又∠MGB=∠MCB+∠GMC，则∠BMA=∠GMC.

又MA=MC，则△MBA △MGC，则AB=GC.

则CD=CG+GD=AB+BD.

点评：归纳是演绎的源泉！

（3）对称法.

解法5：如图6，连接AO、BO、OM.

图6

作OW⊥CB交BC于点F，交圆于点W，作点M关于OW的对称点P，作PH⊥BC交BC于点H，连接OP，OM分别交AC、BC于点E、G.

由∠OFG=∠CEM=90°，∠OGC=∠OGC，得∠ACB=∠FOG.

则∠AOB=∠MOP.

则△POM △BOA.

则PM=AB.

由PH⊥BC，MD⊥BC，得PM=HD.

则AB=PM=HD.

则CD=BH.

则BD+AB=CD.

点评：旋转变换使线段和差问题变得直观、体现对称美.

（4）托勒密定理证法.

解法6：如图7，由“托勒密定理”知AB·MC+BM·AC=AM·BC.

假设AM=MC=m.

AB·m+BM·2mcosα=BC·m.

AB+2BM·cosα=BC.

AB+2BD=CD+BD.

AB+BD=CD.

反思一种解法，归纳这种解法的原理以求类比演绎出同类解法，如补短法.及时归纳补短法自然就会产生另外一类解法——截长法.无论补短还是截长，无非是构造一对全等三角形，除了位置没有特殊要求的构造法，还有位置有特殊要求的对称法.在圆中还有很多定理，如托勒密定理，笔者发现借助托勒密定理可以证得阿基米德折弦定理.此种证法把公元前后不同国度的两位大师紧紧联系在一起！

图7

图8

二、中考题的诞生

如图8，△ABC是⊙O的内接三角形，点D在弧BC上，点E在弦AB上（点E不与A重合），且四边形BDCE是菱形.

（1）求证：AC=CE.

（2）求证：BC2-AC2=AB·AC.

（3）已知⊙O的半径为3.

1.解法欣赏

第（1）问，这里不再赘述.

下面解决第（2）问.

证法1：如图9，过点C作CF⊥AE于F.

点拨：①观察“BC2-AC2”的形式，联想到“勾股定理”，需要构造直角三角形；②由“AC=CE”联想到“等腰三角形三线合一”.

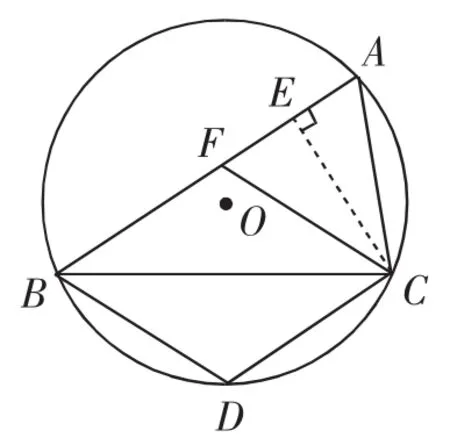
图9

图10

证法2：如图10，延长BA到G，使AG=AC.由∠ACG=∠G=∠ABC，构造△GCA △GBC.

如图11，延长CA到H，使AH=AB，构造△CAB△CBH.

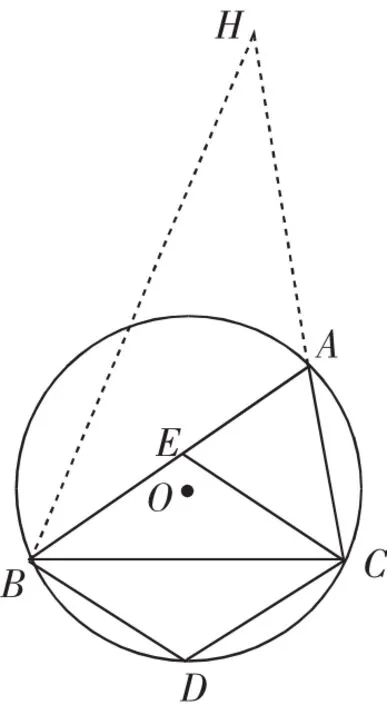
图11

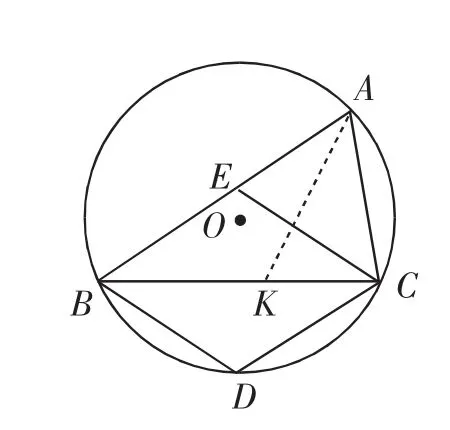
图12

如图12，作∠BAC的角平分线交BC于K，则∠BAK=∠CAK=∠BAC=∠AEC=∠ABC，构造△CAK△CBA.三种构造相似三角形的方法均可证得结论.

对于第（3）问的①，这里不再赘述.

下面解决第（3）问的②.

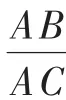
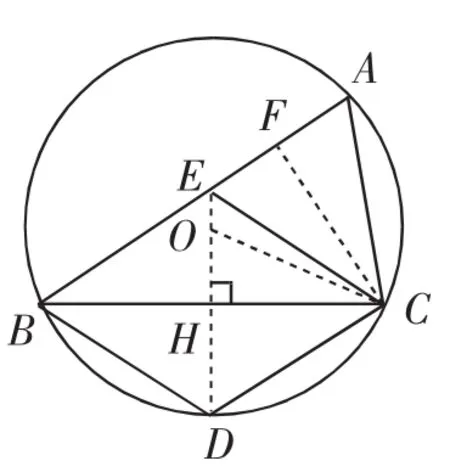
图13

由∠COD=∠A=∠ECD，得△COD △ECD.

所以CD2=OD·DE，即b2=3DE.

则b2=-9m+27，故AB·AC=mb2=-9m2+27m.

解法2：设OH=x，则AB·AC=BC2-AC2=4CH2-CD2=4（9-x2）-［（9-x2）+（3-x）2］=-4x2+6x+18，则当x=时，AB·AC取得最大值.

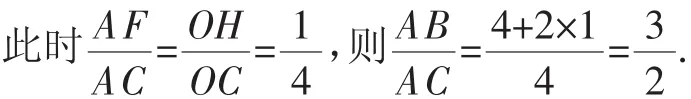
解法3：设cos∠COH=cos∠A==k，则OH=3k，则AB·AC=BC2-AC2=4CH2-CD2=4（9-9k2）-［（9-9k2）+（3-3k）2］=-36k2+18k+18.

2.试题评析

第（1）问主要考查对等腰三角形的判定、圆周角定理、圆内接四边形的性质及菱形的性质的掌握情况，知识内涵丰富，难度不大，在解决阿基米德折弦定理的过程中，构造了一个特殊的四边形——菱形，使本题结论丰富，为中考题的诞生创造条件.以圆为背景，使得弧、弦、角三者相互转化，为问题解决方法的多样性（一题多解）铺设了道路.

在第（2）问要证明的结论中，出现两条线段的平方差形式，学生可以根据学习勾股定理时积累的数学活动经验，把问题表征成：直角三角形中有关边之间关系的问题.这样如何构造直角三角形就成了第（2）问的突破口，这时第（1）问中证得的△ACE是等腰三角形可提供有益的启示，即通过添加等腰三角形中的常见辅助线（底边上的高）构造出所需的直角三角形.另外，学生也可以把所要证明的结论变形成“a2=bc”的形式，这样问题就可表征成：两个相似三角形中有关边的关系问题.如何构造相似三角形成为问题解决的突破口.因此，第（2）问能有效地测出学生能否自觉、合理地运用转化思想及相关的数学活动经验进行数学思考.问题：根据考生反馈，学生对于式子BC2-AC2=AB·AC的变形能力、认知能力、联想能力较弱.由BC2-AC2能联想到构造直角三角形，但是很难构造，将BC2-AC2=AB·AC变形为BC2=AB·AC+AC2=AC·（AB+AC）是比较困难的数感、符号感不强是导致此处思路出现障碍的重要原因.如果能够变形成式子“a2=bc”，受阿基米德原理折弦定理“截长补短法”启发构造相似三角形就是顺理成章的事了.

本题各小问层次分明，梯度合理，内在逻辑明显，有利于学生在各小问的相关启发下拾级而上，也有利于不同层次学生的发挥，具有较好的信度和区分度.另外，本题合理地兼顾了对基础知识、基本技能、基本数学思想方法和基本数学活动经验的考查，能有效地检测出数学抽象、数学推理、数学运算等关键能力的水平.若该题第（3）问将AC改为常量1，难度将下降不少，从而可以更好地考查学生利用函数模型分析问题的能力.

三、教学建议

1.用好教材，构建知识体系

教材是教学的蓝本，是课程标准的具体体现，是呈现数学知识的主要载体.在日常教学中，教师要认真研究教材，充分理解教材编写意图及教学要求，同时要加强与其他知识的横向联系，有意识地引导学生构建知识体系，辅助学生进行知识的高效内化，便于学生审题时站在宏观的角度分析问题、解决问题.要用好教材、用活教材，特别是对教材例题、习题，教师一定要进行充分挖掘，最好能进行多维变式，开阔学生的思路，培养学生的应用意识与创新意识.

2.注重过程，体现主体地位

数学的教学要指向核心素养，而数学学科核心素养的落实不能依赖“短平快”的记忆与模仿，要放慢教学节奏，让学生有充分的、真实的过程性体验.要真正体现学生的主体地位，让学生在经历知识生成的过程中巩固“四基”，在合作交流的过程中积累活动经验，在探究归纳的过程中领悟思想方法，并逐渐内化为自己的经验，形成问题解决的自觉意识.

3.深度教学，发展理性思维

理性思维是数学的核心思维能力，同时是人格素养的重要部分.发展理性思维、培养理性能力是数学学习的核心任务.教师要通过深度教学来发展学生思维的深度和广度，引导学生深入问题本质，提高学生的横向综合能力和纵向突破能力.教师要在理解数学、理解学生、理解教学的基础上发挥好主导作用，将数学知识、技能和数学思想方法有机结合在一起，给学生提供展示数学思维能力的平台，彰显数学教学对学生数学思维能力发展的价值.

4.注重归纳，探索自然解法

追溯中考题的来源，剖析归纳其解法可知：归纳是演绎的源泉.只有做好题后总结归纳，才能演绎出新的解题思路，做好演绎，才能锻炼我们的数学思维.可见归纳与演绎是相辅相成的，只有做到追根溯源，才能达到道法自然的解题境界.