例说“拼图法”在初中数学解题中的应用

☉山东省济南市莱芜区雪野镇中心中学 朱玉平

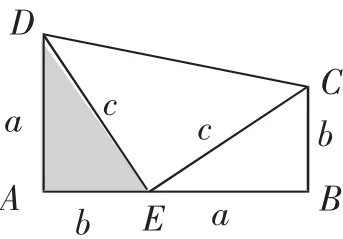
图1

图2

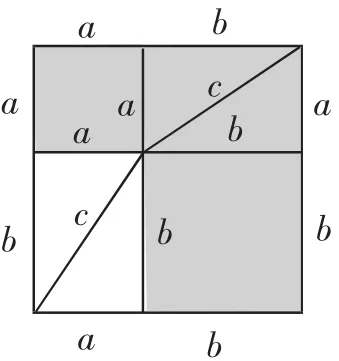
图3

图4

一、求代数式的值

例1已知一个长方形的长与宽的和为7，面积为10，求该长方形的长与宽的差的平方.

本题若按常规方法，可设长方形的长为a，宽为b.根据题意，得a+b=7，ab=10.而长与宽的差的平方为（a-b）2.要求（a-b）2的值，可将（a-b）2变形为含有a+b和ab的式子.即（a-b）2=a2+b2-2ab=（a2+b2+2ab）-4ab=（a+b）2-4ab=72-4×10=49-40=9.

除了上述解法，也可运用拼图法巧解.将四个大小一样的长方形按照图5所示的方式拼在一起，正好拼成一个大正方形，这个大正方形的边长正好是长方形的长与宽的和，它的中间是一个小正方形，其边长正好是长方形的长与宽的差.要求长方形的长与宽的差的平方，只要求出小正方形的面积即可.观察图5可以发现，大正方形的面积减去4个长方形的面积即为小正方形的面积.即S小正方形=S大正方形-4S长方形=72-4×10=49-40=9.所以长方形的长与宽的差的平方为9.这种解法显然是对常规解法的创新，展现了用“拼图法”解决数学问题的魅力.

牛刀小试：已知一个长方形的长与宽的差为2，面积为35，求该长方形的长与宽的和的平方.

图5

图6

二、求两角的和

例2三个大小一样的正方形按照图6所示的方式拼在一起，你能求出∠1+∠2的大小吗？

本题实际上是求直角边长分别为1个单位、2个单位的直角三角形中最小锐角与直角边长分别为1个单位、3个单位的直角三角形中最小锐角之和.显然tan∠1=，tan∠2=.如果利用两角和的正切公式，不难得到=1.而∠1+∠2＜180°，则∠1+∠2=45°.由于初中阶段我们没有学过两角和的正切公式，需要另辟蹊径.既然要求的是两角之和，我们可以将∠1、∠2按图7所示的方式拼在一起，则∠BAD=∠1+∠2，接下来只需求出∠BAD的大小即可.一时半会仍然找不到求∠BAD的办法.观察图7我们发现，如果连接BD，那么△BAD刚好构成一个等腰直角三角形.证明过程如下.由勾股定理易知AD2=12+22=5，BD2=12+22=5，AB2=12+32=10.则AD=BD，AD2+BD2=AB2，由勾股定理的逆定理知△BAD是直角三角形.则△BAD是等腰直角三角形.则∠BAD=45°，即∠1+∠2=45°.当然在证明△BAD是等腰直角三角形时，也可通过三角形全等证明，即先证△BCD △DEA，则∠BDC=∠1，BD=AD.则∠ADB=∠BDC+∠ADE=∠1+∠ADE=90°.则△BAD是等腰直角三角形.

牛刀小试：如图8，在Rt△ABC和Rt△DEF中，∠C=∠F=90°，AC=3cm，BC=4cm，DE=3cm，EF=2cm.求sin（∠E-∠B）的值.

图7

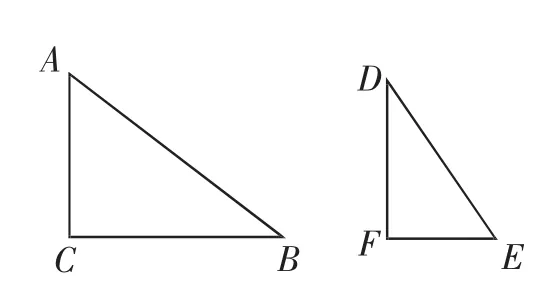
图8

三、证明几何命题

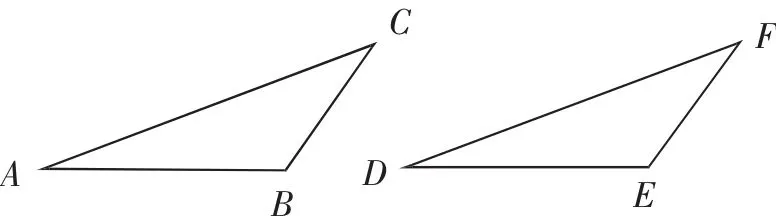
图9

图10

图11

上述证法是将钝角所对的相等的边AC与DF拼在一起，也可以将锐角所对的相等的边AB与DE拼在一起.如图11，将AB与DE拼在一起，使点A与点D重合，点B与点E重合，且使∠C与∠F分别在AB（或DE）的两侧.连接CF.证明过程留给读者完成.

事实上，满足“两边及其中一边的对角对应相等的两个三角形”，当其中一边的对角是钝角时，这两个三角形全等，当其中一边的对角是直角时，这两个三角形也全等.证明之时，既可将斜边拼在一起，也可将直角边拼在一起.

牛刀小试：如图12，在Rt△ABC和Rt△DEF中，∠C=∠F=90°，AB=DE，AB＞BC，DE＞EF，且AC-BC=DF-EF.那么Rt△ABC和Rt△DEF全等吗？请说明理由.

图12

“拼图法”在解决初中数学问题中的应用还有很多.再如，如图13，分别以△ABC的三边为边在△ABC外部作正方形ACDE、正方形ABMN、正方形BCPQ.如果这三个正方形的面积分别为370、74和116，试求△ABC的面积.由于△ABC的三边都为无理数（），直接求解比较困难.我们可以观察三个正方形的面积特征：74=52+72，116=42+102，370=92+172，由这些特殊的数正好可以拼合成图14，这样可以便捷求出△ABC的面积.

图13

图14

从以上几例不难看出，运用“拼图法”解决数学问题，确实可以起到化难为易、化繁为简、事半功倍之效，展现了用“拼图法”解决数学问题的魅力.希望大家认真领会“拼图法”，并在解决数学问题时尝试应用“拼图法”，让“拼图法”成为我们解决数学问题的一项技能.W