一道有关圆的试题的多种思路

☉湖北省武汉市左岭第一初级中学 王晓霞

波利亚在《数学的发现》序言中说：“中学数学教学的首要任务就是加强解题训练.”他还有一句脍炙人口的名言：“掌握数学就意味着善于解题.”解题教学在中学数学教学中占有极其重要的地位，一题多解是培养学生思维灵活性与创造性的重要途径.笔者对武汉市2017年元月调考第21题进行研究，有些心得，现整理如下：

一、原题呈现

（2017年武汉市元月调考第21题）如图1，在Rt△ABC中，∠BAC=90°，BD是∠ABC的角平分线，以点D为圆心，DA为半径的⊙D与AC相交于点E．

（1）求证：BC是⊙D的切线；

（2）若AB=5，BC=13，求CE的长．

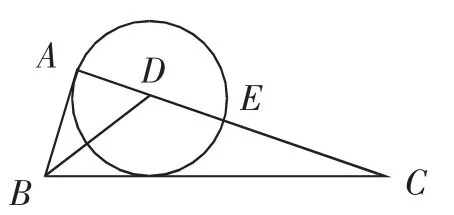
图1

二、试题总体评析

该题涉及的主要知识点有：角平分线的性质、直线与圆的位置关系、切线的判断方法、切线长定理、勾股定理、比例的计算等；涉及的基本方法有：线段、角之间的关系的转化，列表达式进行计算，考查学生对基础几何问题的逻辑推理、规范书写及简单计算的能力.本题的定位虽然是一道基础几何题，涉及的知识点也并不复杂，但是从最后的阅卷报告中发现，满分为8分的试题，实际平均分才4.82分，得分率仅为60.25%，满分率也只有44.57%.由此可见，学生对于此类几何逻辑推理题的掌握并不理想，部分学生的书写缺乏规范性，与此同时，也涌现出了不同的解题思路.

三、典型错误及成因分析

该题要求学生正确、完整地写出解答过程，考查学生的几何推理能力、简单计算能力及规范书写能力.笔者将典型错误归类如下：

1.第（1）题的典型错误及分析

错证1：如图2，过点D作DF⊥BC于点F，直接将∠ABC当成60°，然后DF=BD，同时ADBD，得到DF=AD，然后得到结论BC是⊙D的切线.

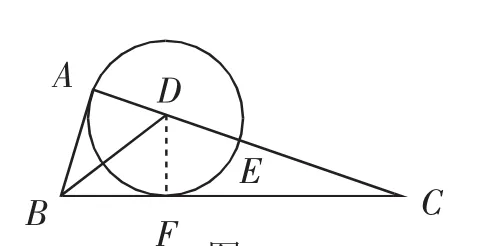
图2

【分析】这种错误主要是没有认真审题，仅依靠自己的主观感受，盲目判断造成的.题目中并未给出∠ABC=60°这个条件，出现这种错误的考生相当于把题目中的条件特殊化了，这种做法是不符合严格推理要求的.

错证2：如图2，过点D作DF⊥BC于点F，使DF=AD，得到结论BC是⊙D的切线.

【分析】这种错误属于人为造条件，过点D作DF⊥BC于点F，即线段DF的长度已经确定了，如何使DF=AD？这种错误就属于随意制造条件.

2.第（2）题的典型错误及分析

错解1：利用勾股定理进行计算时，解错方程，得到错误的结论.

错解2：利用相似处理时，三角形的对应顶点没有写对，导致对应边错位，得到错误的结论.

【分析】第（2）题的错解1是由于学生的计算功底不扎实，或者还没有熟练掌握初中阶段应该掌握的各种类型方程的解法，基本技能不过关.第（2）题的错解2是由于答题时缺乏规范性，导致得不到正确解而失分.这两种错误都属于比较低级的错误，但是在实际的考试中学生经常犯这样的错误，所以一定要抓好“双基”的落实，严格要求学生解题时要规范.

四、多种思路及其分析

笔者重点对第（2）题的求解进行分析.

思路1：如图2，设圆的半径为r，根据第（1）题的辅助线，在Rt△DFC中，CD=12-r，DF=r，CF=13-5=8，利用勾股定理建立方程82+r2=（12-r）2，解得r=，则CE=12-2r=

【分析】思路1是命题者在命制试题时的意图，也是学生解题时的自然思路.设未知数，利用勾股定理建立等量关系，解方程，这种解法是学生比较熟悉的方法，大部分学生都用到了该思路.

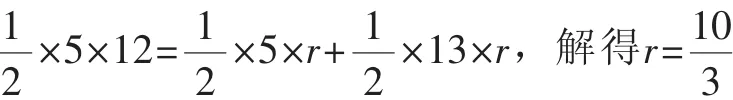
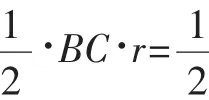
思路4：如图3，过点C作圆的切线与BA的延长线交于点H，连接DH，过点D作DG⊥CH于点G，则点G为切点.

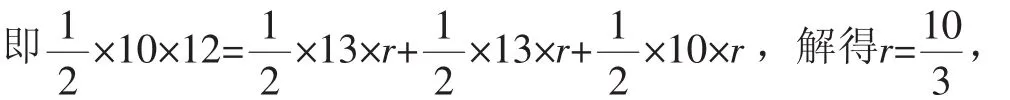
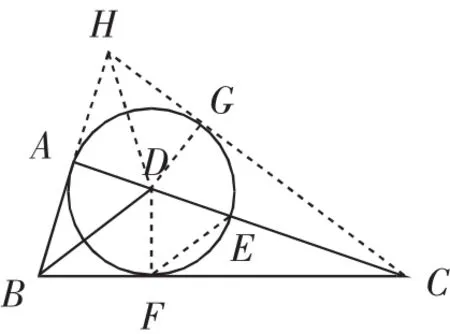
图3

【分析】思路2～4都利用了等积法，但是思路4较思路2和3稍显复杂，需要作的线太多，而且作了一条不经常用的辅助线，即作切线，暂且不论繁简程度，若推理过程严谨，也不失为一种好的解法，体现了殊途同归的解题思维本真.

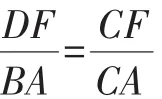
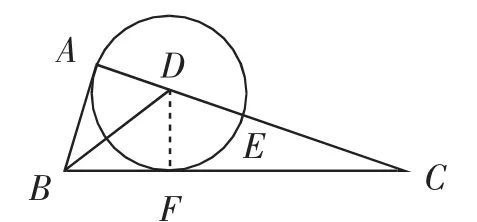
图4

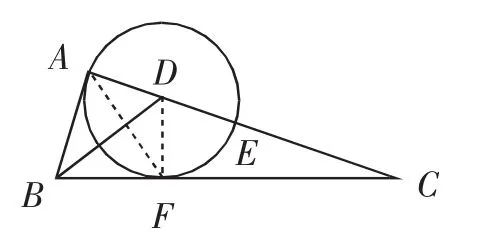
图5

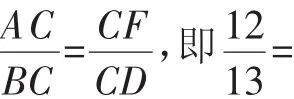
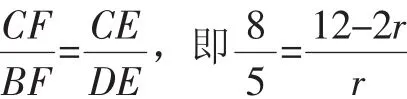
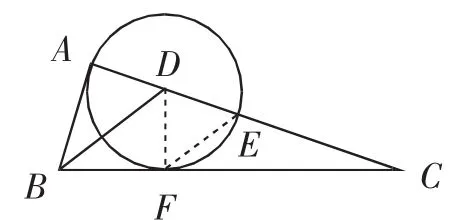
图6

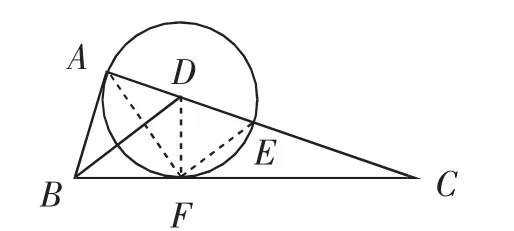
图7

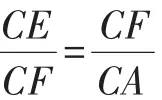
【分析】思路5、6、8均需添加辅助线，构造相似，利用相似得到比例线段，从而求出关键线段，达到解决问题的目的.思路7利用平行线分线段成比例定理计算圆的半径，从而解决问题.其中涉及四点共圆、同弧所对的圆周角相等、切线长定理、证两三角形相似的方法、平行线分线段成比例等基础知识储备.

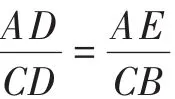
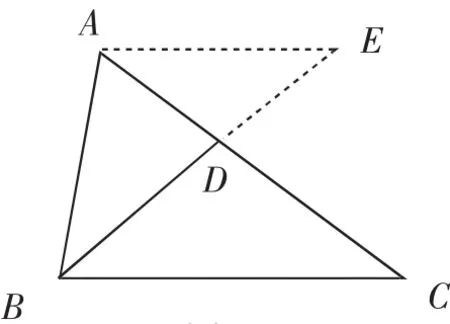
图8

【分析】思路9需要一定的知识储备，即要熟悉三角形的角平分线定理，对比前几种思路，不易想到.但仔细想来，仍然是作平行线构造相似，得到比例线段的关系.联系平时的教学，教师在教学中如能让学生多掌握一种思路，就能拓宽学生的思维，从而使学生能够高屋建瓴地理解问题、解决问题.

五、反思

一题多解的探寻可以拓宽学生的思维宽度，使学生思考问题的角度更多，发散学生的思维，同时激发学生的学习热情.本题作为一个比较基础的题目，仍然涉及转化、数形结合、方程、建模等思想，通过数学思想的培养，数学能力才会有大幅度的提高.掌握数学思想，就是掌握数学的精髓，促进学生思维的可持续发展.W