明辨主元防控错漏，积极践行“化错教学”——对一道期末把关题的阅卷与思考

☉江苏省海安市李堡镇丁所初级中学 张海华

本地区九上期末试卷最后一题是一道关于“好点”的新定义考题，笔者参加了该题的网上阅卷工作，对这道考题出现的不同解法有了较多的观察和评价，阅卷之后也对较难的小问进行了深入思考，本文先梳理出来，与大家分享、研讨.

一、考题及阅卷记录

考题：（江苏省海安市九上期末卷，第28题，全卷最后一题）如图1，点P在直线y=x-1上，设过点P的直线交抛物线y=x2于A（a，a2）、B（b，b2）两点，当满足PA=AB时，称点P为“优点”.

（1）当a+b=0时，求“优点”P的横坐标.

（2）若“优点”P的横坐标为3，求式子18a-9b的值.

（3）小安演算发现：直线y=x-1上的所有点都是“优点”.请判断小安的发现是否正确.如果正确，请说明理由；如果不正确，请举出反例.

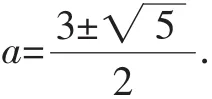
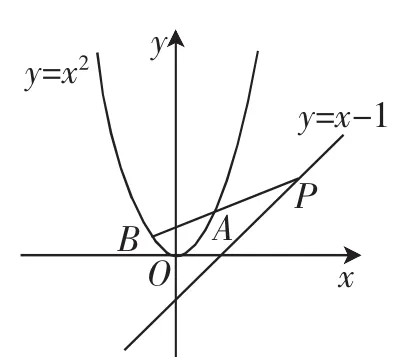
图1

对于第（2）问，学生的方法很多，以下提供比较简洁的思路.由点P在直线y=x-1上，得点P的坐标为（3，2）.由PA=AB，得3-a=a-b，整理得2a-b=3，所以18a-9b=9（2ab）=27.

从阅卷情况看，少数学生错误引用第（1）问的条件也可求出结果27，但根据评分组研讨的意见，这种情况不能得分，因为这说明考生没有弄清各小问之间的强化条件是不可以交叉引用的.

对于第（3）问，先给出命题组预设的参考答案.设点P的坐标为（k，k-1），结合点A的坐标（a，a2），当PA=AB时，分析出点B的坐标为（2a-k，2a2-k+1）.把点B的坐标代入抛物线的解析式y=x2中，得2a2-k+1=（2a-k）2，整理成关于a的一元二次方程（即视a为主元），得2a2-4ka+k2+k-1=0.Δ=（4k）2-4×2（k2+k-1）=8（ k-）2+6＞0.所以对于任意k，总有a使得PA=AB.即直线y=x-1上的点均为优点.

阅卷过程中，方法2也给了全分，记录如下：

方法2：设点P的坐标为（x，x-1），结合点A的坐标（a，a2），当PA=AB时，分析出点B的坐标为（2a-x，2a2-x+1）.把点B的坐标代入抛物线的解析式y=x2中，得2a2-x+1=（2ax）2，整理得x2-（4a-1）x+2a2-1=0.Δ=（4a-1）2-4（2a2-1）=8（ a-）2+3＞0.对于任意a，总有x使得PA=AB.故直线y=x-1上的点均为优点.

但是与方法2类似的方法3就没有得出最后结果，整理如下：

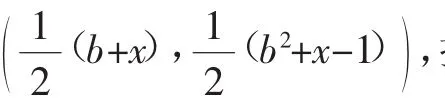
整理成关于x的一元二次方程（即视x为主元），得x2+（2b-2）x+2-b2=0.Δ=（2b-2）2-4（2-b）2=8（ b-）2-6＞0.对于任意b，并不能保证x一定有实数根，所以直线y=x-1上的点不一定都为优点.

究错：方法3与方法2本质上是一致的，为什么两种方法导致不同的判断呢？让我们先退回方法2，将其与方法1进行比对，就会发现，方法2、方法3的问题出在主元辨识不当.方法2只是运算下来，恰好也出现以x为主元的方程根的判别式大于0；但是若以点B的坐标表示点A，仍然运用方法2的思路，则会出现方法3中以x为主元的方程根的判别式并不一定大于0.比如Δ=8（ b-）2-6出现后，就会导致思路受阻，造成错误判断.

比如，我们可以对方法2做出改进，将其所得到的方程整理成关于a的一元二次方程，得2a2-4xa+x2+x-1=0.Δ=（4x）2-8（x2+x-1）=8（ x-）2+6＞0.所以对于任意x，总有x使得PA=AB.直线y=x-1上的点均为优点.

同样，我们对方法3做出改进，将其所得到的方程整理成关于b的一元二次方程，得b2-2xb-x2+2x-2=0.Δ=（2x）2-4（-x2+2x-2）=8（ x-）2+6＞0.所以对于任意x，总有x使得PA=AB，故直线y=x-1上的点均为优点.

这样，就看出三种方法中计算根的判别式，配方出非负形式的结果是一致的.

此外，还有个别考生有如下解法，也是可行的，只是运算量陷入繁杂处境，摘抄如下：

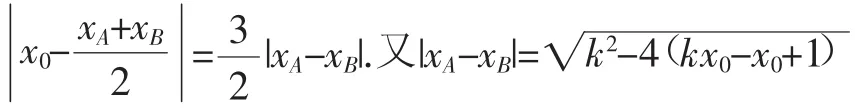
二、由考题批阅引发的教学思考

1.二次函数教学要重视“根的判别式”的价值

笔者结合多年毕业班教学经历，发现近些年二次函数教学受到有些不良试题（比如以抛物线为背景，实质上是探究平面几何的复杂构造，与二次函数及性质并不相关）的影响，训练的方向有些偏差.本文中这道考题以探求新定义“好点”为背景，本质上是设出参数，并转化为一元二次方程，根据题意准确选定主元后利用一元二次方程根的判别式来攻克难点.由于平时这方面的题型训练不足，或对根的判别式在二次函数中的重要性认识不足，使得一些复习训练出现薄弱环节，这也提醒我们，在二次函数教学过程中，对根的判别式要有更丰富、更深入的认识.

2.含参数的二次方程要注意引导学生明辨主元

含参数的二次方程关键在于明辨主元，选定主元后再计算根的判别式才能奏效.上文中提到的方法2、方法3，其不足就在于主元辨识不清，只是方法2中恰好任意的a值也满足方程x的解，相应的，也就是x可以取得任意实数解，也能实现判断，但这种主元辨识不清的思路对方法3就不灵了，因为并不是任意b的值都能满足关于x的方程.现在可回顾一下这问的本质就是：b=2a-x，而x、a需要满足关系式x2-（4a-1）x+2a2-1=0.尽管变量a、x的范围是任意实数，但是需要组合出现并代入b=2a-x中，从而就使得b的值域不是实数集.

3.开展究错教学要从简单纠正答案到探究错因

小学著名特级教师华应龙老师近年来倡导的“化错教学”，从纠错、究错走向融错、化错，也是值得我们初中老师在课堂教学中积极践行的.具体来说，当我们在讲评本文考题的几种典型错漏时，如何引导学生参与辨析上述方法2、方法3的不足，并指出它们的改进意见是基于问题条件中哪些关键信息得到的，这些都可以作为课前预设，在习题讲评过程中引导学生参与进来.对于特别优秀的学生，如果能让他们自主发现并诊评这些十分隐蔽的错漏，对于学生数学素养的提升是非常有好处的.

三、写在后面

教学即研究，阅卷即研究，用研究的眼光看待看似枯燥乏味的阅卷工作，收集素材并跟进解读、诊评，并把相关素材收集起来作为试卷讲评过程中的教学资源，都是值得开展研究的.需要说明的是，文中观点与阐释并不一定准确，更不一定正确，敬请同行批评指正.

致谢：本文中学生答题的素材整理、解法研讨、后期成文的全过程都得到海安市教师发展中心初中数学教研员刘东升老师的悉心指导，谨致谢意！