践行问题驱动教学：从习题走向“问题”

☉江苏省苏州工业园区星汇学校 李艳敏

从深刻理解初中数学知识来看，初中内容多属于几百年之前的数学内容，而且有很多数学习题的“历史”也很长，有老师提出数学教学中对于例、习题的选择不宜过分追所谓的“网红题”是有一定道理的.结合多年教学经验，笔者认为，“经典问题”（本文所提出的“经典问题”是指在不同时期教材上都曾出现过的一些例、习题）的教学研究是值得大家重视的.本文结合两则习题教学通过改编设计成“问题”教学的案例，展开对“经典问题”教学的思考，供研讨.

一、从习题走向“问题”的教学案例

案例1：平行与平分的组合图形教学.

习题1：如图1，已知∠ADE=70°，DF平分∠ADE，∠1=35°，求证：DF∥BE.

证明：∵DF平分∠ADE（已知），

∵∠ADE=70°（ ），

∴________=35°.

∵∠1=35（° ），

∴_____=_____（ ）.

∴_____（ ）.

图1

教学组织：如果安排学生练习之后核对答案，并弄清每一步的推理依据就完成该题的教学，则是典型的“入宝山而空返”（罗增儒 语）.教过多年七年级的老师（或者练习多本不同练习册也有此体会）会知道，这是一个经典图形，考查角度、变式设问多样.如何实现这个“经典图形”教学效益的最大化？有如下一些建议：

问题1：如图1，已知∠ADE=68°，DF平分∠ADE，∠1=34°，求证：DF∥BE.

先安排学生独立思考，学生贯通思路后，分别请两个学生上台讲解思路，再由各个学生书写过程，并投影批改.

接下来，跟进系列变式，促进学生深入思考、学深、学透、学活：

变式1：（一般化）如图1，已知∠ADE=2∠1，DF平分∠ADE，求证：DF∥BE.

教学组织：学生练习之后，教师指出原问题中的34°、68°只是揭示了∠ADE=2∠1，并无其他特别意义.

变式2：（条件、结论置换设问）如图1，已知∠ADE=2∠1，DF∥BE，求证：DF平分∠ADE.

变式3：（增加解题层次设问）如图1，已知∠ADE=2∠1，DF⊥AC，BE⊥AC，求证：DF平分∠ADE.

变式4：（增加解题层次设问）如图1，已知∠ADF=∠EBC，DF⊥AC，BE⊥AC，求证：BE平分∠ABC.

最后，还可安排班级前三分之一水平的学生由这个图形编拟一道几何证明题，其余学生整理上述问题及系列变式的解题思路、完善课堂笔记.

随想：“习题1”这样的填空题在很多教辅资料或习题单式的导学案中经常出现，如果我们在备课时，将其开发成问题串式的题组，以系列变式与追问的形式呈现（或成果扩大式的问题设计），就是真正用心在备课了，否则备课时只是选题填满一张8开纸的习题单式学案印发，教师本人也只是无趣的重复劳动，教学即研究终是一句空话.

案例2：正方形经典习题教学.

习题2：如图2，点E为正方形ABCD的边BC的中点，连接AE，作∠AEF=90°，交正方形的一个外角平分线于点F.求证AE=EF.

教学组织：这道习题不少教师讲评之后都会针对点E进行位置变式，达到一题多变的教学追求.事实上，除了一题多变，这道习题还有很多不同解法，即一题多解也应该在这道习题教学时得到体现.以下就围绕这道习题进行系列设计.

问题2：如图2，点E为正方形ABCD的边BC上任意一点，连接AE，作∠AEF=90°，交正方形的一个外角平分线于点F.求证AE=EF.

教学组织：独立思考后，很多学生容易想到一种思路，即如图3，在AB上截取BM=BE，构造等腰直角三角形BME，再证△AEM △ECF即可.这时可预设以下两种思路，“留白式”提供给学生完善思考.

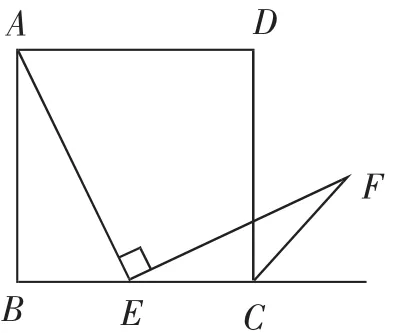
图2

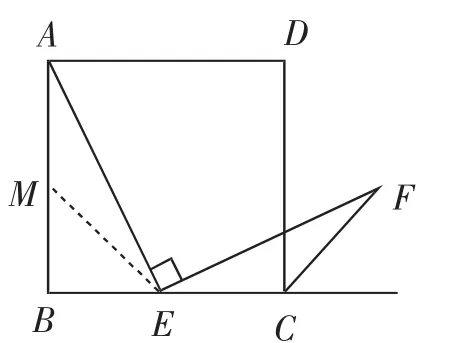
图3

小明的思路：如图4，在AB的延长线上截取BN=BE，构造等腰直角三角形BNE……进一步可以证明四边形CFEN是平行四边形……

小敏的思路：如图5，连接AC，作EG∥AB，交AC于G点……

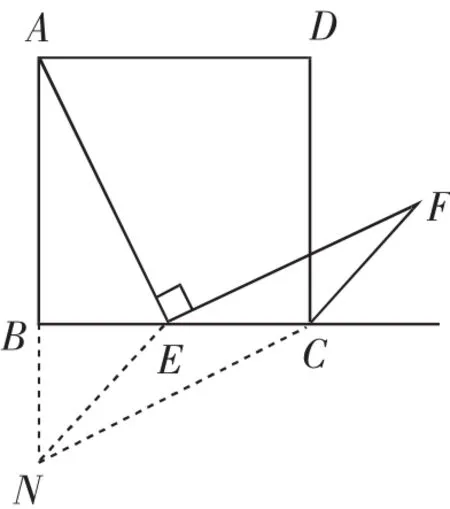
图4

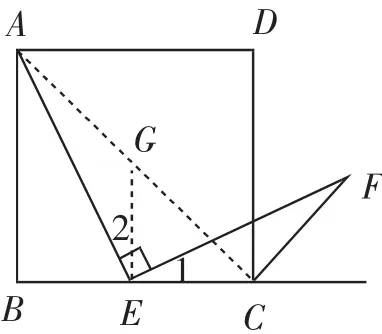
图5

教学组织：安排学生阅读理解之后，完善“小明的思路”“小敏的思路”，先在小组内交流，再由小组推荐一个学生代表在全班汇报展示他们对“小明的思路”“小敏的思路”的补充与完善.

问题变式：当点E在线段BC的延长线上时，其余条件不变，继续研究AE与EF的数量关系.

拓展问题：如图6，将正方形ABCD放在平面直角坐标系中进行研究，设点B与坐标原点重合，正方形的边长为2.点E（m，0），连接AE，以AE为一条直角边作等腰直角三角形AEF，使∠AEF=90°.设点F的坐标为（x，y），分析y与x之间的函数关系式.

设计意图：通过变式问题与拓展问题，使得该题的教学功能得到大大加强，学生对这类正方形问题的深层结构也有了更深的理解.

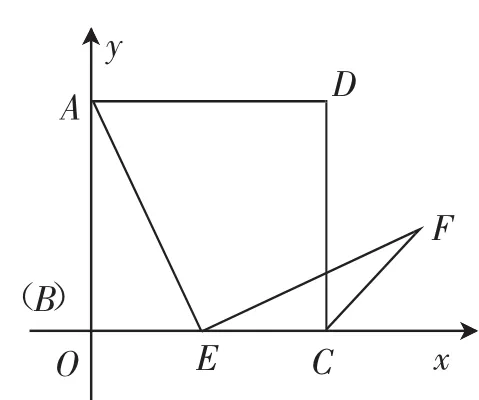
图6

二、关于经典问题教学的进一步思考

1.深刻理解教学内容，精准选取经典问题

当前不少数学教育研究者都积极倡导在深刻理解数学的基础上开展数学教学内容的选择和课堂教学设计，否则用力过多就有可能走偏方向，因为作为“教什么”的教学内容永远是第一位的.所以关于经典问题的选取，需要基于我们对初中数学教学内容的深刻理解，找准一些经典问题或经典图形，并从不同角度进行改编变式或生长拓展.上文“习题1”就是这样的经典问题，并且该题的图形也是一个经典图形.从这个意义上说，能精准识别（也即“看得出”）经典问题也是需要“眼力”的.

2.基于年级学情出发，精心预设变式问题

在选定“经典问题”之后，就需要针对这些问题进行变式改编与生长拓展.这里需要从学生已有解题经验出发，想清学生所在年级，已学习哪些章节，有了哪些知识基础，然后选定一个相对简单的问题，让绝大多数学生都能顺利解决.这一点非常关键，因为我们常常见到有些导入问题非常繁杂，多数学生在处理这类问题的初始阶段就被“拒之题外”，对后续变式改编、生长拓展的参与和研究非常不利.上文中“问题2”是学生在学习正方形之后非常熟悉的一类几何习题，在学习全等时就有相关辅助线构造的经验.所以选择从这个问题出发，学生分组讨论之后再开展变式改编就是基于学情而精心预设的.

3.从习题走向“问题”，践行问题驱动教学

从上文案例梳理可以看出，我们先呈现的是“习题”，然后改编设计成“问题”，一字之别，意义重大.从习题走向“问题”，背后是解题教学价值观的不同.具体来说，习题教学往往是浅层的，上一题讲评之后接着是下一题，属于应试教学的题海训练；而“问题”教学就是开展“问题驱动”教学，带有研究性味道，是引导学生从熟悉的问题背景出发，用“探索未知世界”的方式去研究新问题、不同视角的问题，就解题教学来说，实现了“成果扩大”的追求，教学品质显然更高一些.

三、写在后面

最近看到朋友圈一些同行转发的某知名教育学专家一句话“他们都往大处做，往高处走，我估计了一下自己的能力，觉得自己只能往小处做，往深处走”，深有同感.对于一线教师来说，每天面对最多的就是习题，解题、批改作业、选题、编题、讲评是教学常态，要把每天都在做的“习题”研究想深、想透，让我们选题的眼力再敏锐一些，然后从习题教学走向“问题”教学.想来，我们要修炼的专业基本功（比如，深刻理解数学、理解学情、理解教学、命题能力等）还有很多.