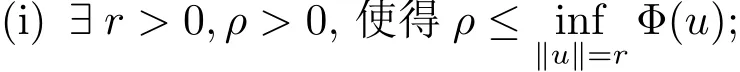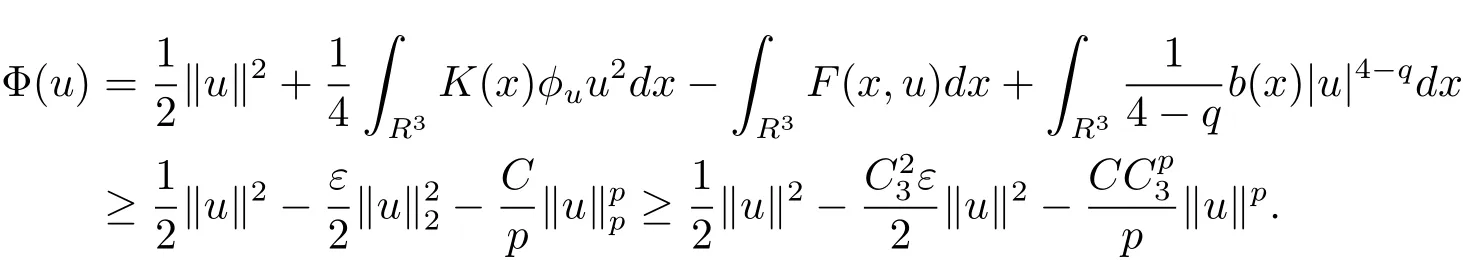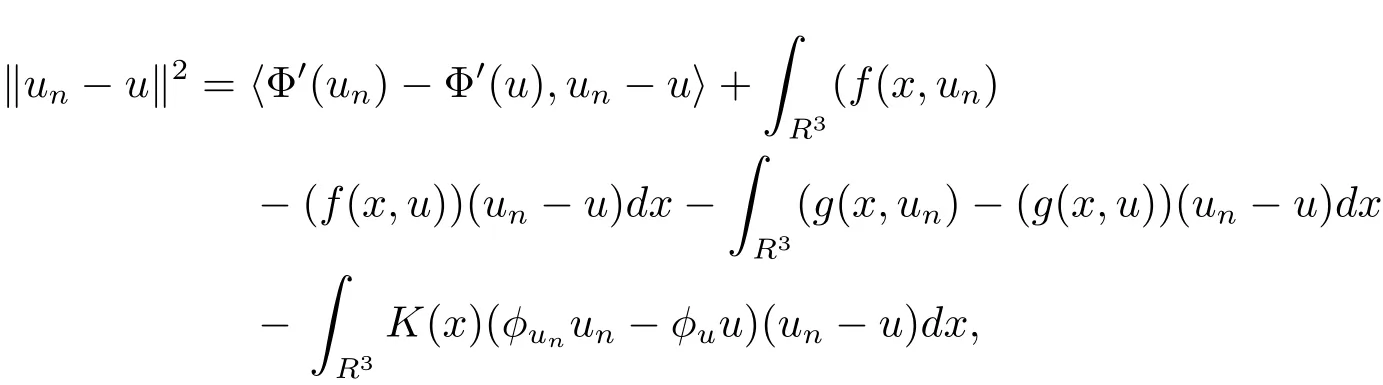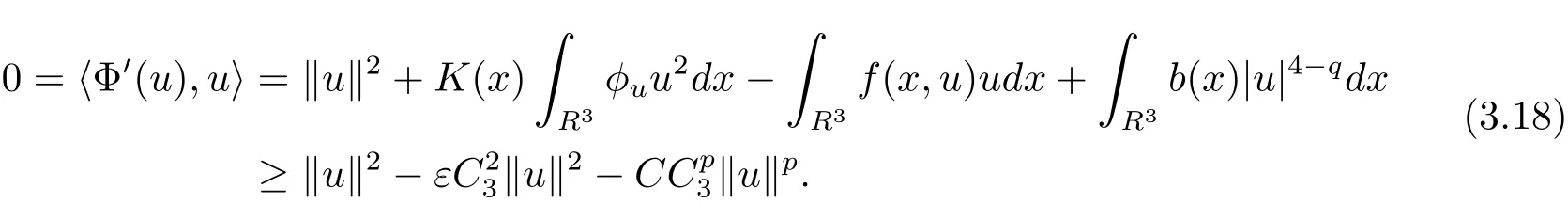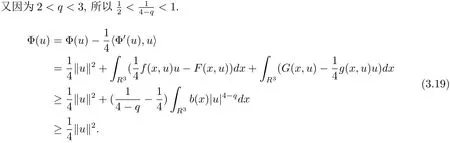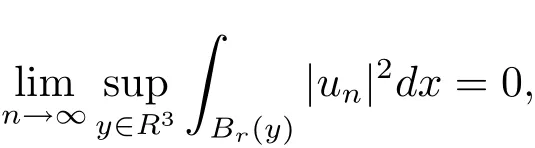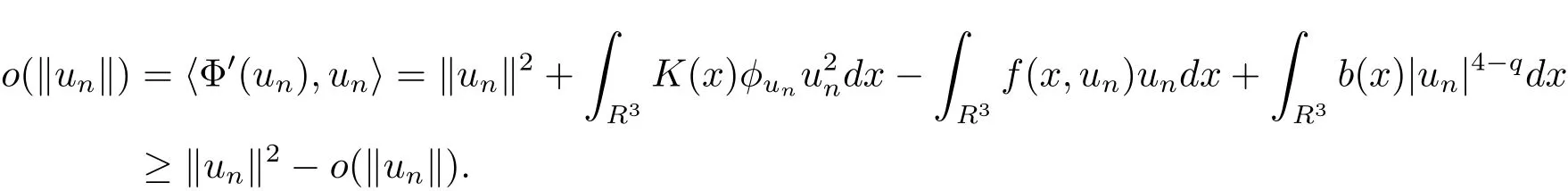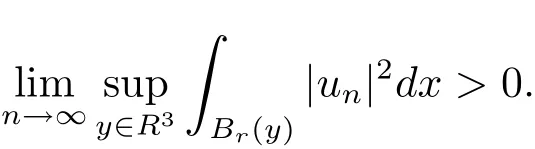非线性SCHRDINGER-MAXWELL方程的基态解
姜影星,黄文念
(广西师范大学数学与统计学院,广西桂林 541006)
1 引言
考虑下面非线性的schr¨odinger-Maxwell方程
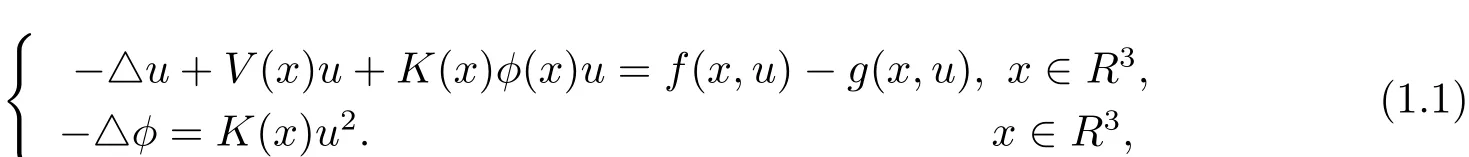
自从系统(1.1)在文献[3]中提出以后,很多学者对系统解的问题产生了兴趣并进行了研究.在文献[1]中,Sun用变化的喷泉定理得出了一类次线性项schr¨odinger-Maxwell方程的无限多个解.在文献[2]中,Li,Su,Wei用变化的喷泉定理得出了非线性schr¨odinger-Maxwell方程的无穷多个高能解的存在性.受文献[2]的启发,本文在文献[2]的非线性项f(x,u)(见本文定理1.1的(f1)–(f4)条件)的基础上,添加了一个次线性项g(x,u)(见定理1.1的(g)条件),将文献[1]中的次线性项0 定理1.1假设V,K和非线性项f,g满足如下条件: (V)V∈C(R3,R)且进一步地,∀M>0,有meas{x∈ R3:V(x)≤ (K)K ∈L∞(R3,R),且K(x)≥0,∀x∈R3. (f1)f∈C(R3×R,R)且存在a>0,p∈(2,6),使得|f(x,u)|≤ a(1+|u|p−1),∀(x,u)∈R3×R. 对于任意的1≤r<∞,Lr(R3)表示通常意义下的Lebesgue空间,其范数为 H1(R3)则表示通常意义下的Sobolev空间,其范数取为 定义如下空间 其范数取为 2∗=6为三维空间的临界Sobolev嵌入指数,则D1,2(R3),→L2∗(R3),C1是最佳嵌入正的常数,即 由Lax-Milgram定理(见文献[13]),∀u∈ H1(R3),∃唯一的φu∈D1,2(R3)使得 进一步地有 从而φu≥0.∀u∈H1(R3),由式(2.1),(2.2)和H¨older不等式知 令 和 在空间E×D1,2中定义一个泛函I, 则I是有意义的,且I∈C1(E×D1,2),同时,I的每个临界点就是系统(1.1)的一个解(这里是指弱解).由式(2.2)得出 易知Φ∈C1(E,R)且 由临界点理论及变分法知:当u∈E为泛函Φ的一个临界点,则(u,φu)为系统(1.1)的一组解.对应的Nehari流形为 定义2.1(见文[14])设E是Banach空间,Φ∈C1(E,R),c∈R.泛函Φ满足(PS)c条件是指:∀{un}⊂E使得 有一个收敛的子列. 定理2.2(见文[15])设E是Banach空间,E∗为其对偶空间,若Φ∈C1(E,R)且满足 其中 ρ>0,r>0,以及v∈E且kvk>r.令c≥ ρ 且是从 0 到v的连续曲线.其中Γ={γ∈C([0,1],E):γ(0)=0,γ(1)=v},则存在{un}⊂ E,使得Φ(un)→c>0且Φ0(un)→0,若Φ满足(PS)c条件,则c≥ρ是Φ的临界值. 引理3.1在定理1.1的假设条件下,则 (ii)∃v∈E,满足kvk>r,使得Φ(v)<0. 证 (i)由(f2)条件知∀ε>0,∃α>0,使得∀x∈R3,0≤|u|≤α,以进 一步得出 因此 结合式(3.2),(3.3),∀x∈R3,u∈R,有 结合式(3.1),(3.4),∀x∈R3,u∈R,有 结合(g)条件和式(2.6),有 (ii)由(f3)条件知∀M>0,∃δ>0,使得|u|≥δ时, 从而 由(f1)条件知∃M1>0,使得有 从而 结合式(3.7),(3.9),(3.11),∀M>0,∃M1>0使得∀有 由式(2.4),(2.6),2 取M充分大,则Φ(te)≤0,取v=te,当t充分大时,kvk>r,使得Φ(v)≤0. 引理3.2在定理1.1的条件下,Φ的(PS)c序列有界. 即{un}有界. 引理3.3在定理1.1的条件下,Φ的有界(PS)c序列收敛,即Φ(un)→c,Φ0(un)→0,则{un}存在一个收敛的子列. 证 因为{un}⊂E有界,所以∃u∈E,使得un*u,由(V)条件知,在Lt(R3),t∈[2,6)中,有 因为 显然,当n→∞时, 因为在Ls(R3),2≤s<6中,有H¨older 不等式, 所以 类似的 因此 则已证∀c,Φ的(PS)c条件成立.因此至少存在一个非零解u∈E,Φ(u)=c,Φ0(u)=0.由式(2.9)知,显然N 非空,∀u∈N,有 由N 的定义,显然u 6≡0,取ε充分小,则 引理3.4(见文[14])设r>0,如果{un}⊂H1(R3)有界,且 则∀s∈(2,6),在Ls(R3)中有un→0. 定理1.1的证明 设{un}⊂N 是Φ的一个极小化序列,则{un}有界,而且通过一个恰当的Z3变换,∃u∈N,使得
2 相关记号和准备工作

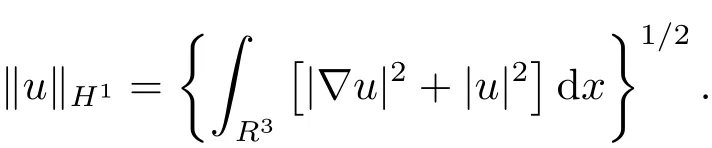
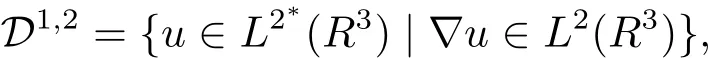
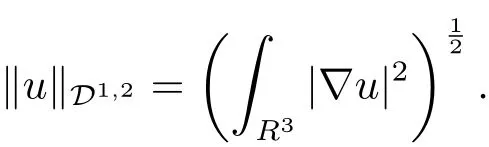


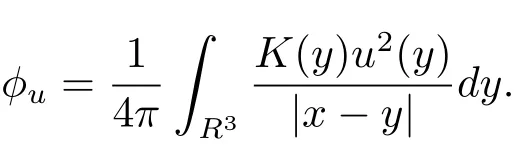
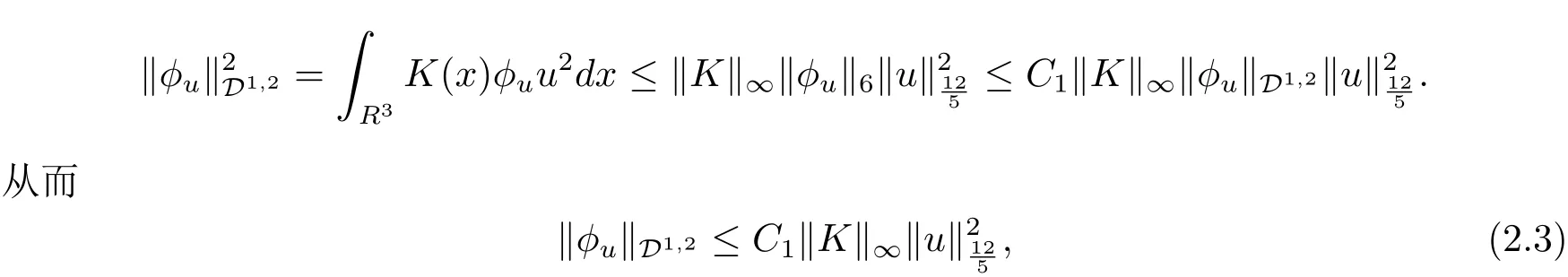
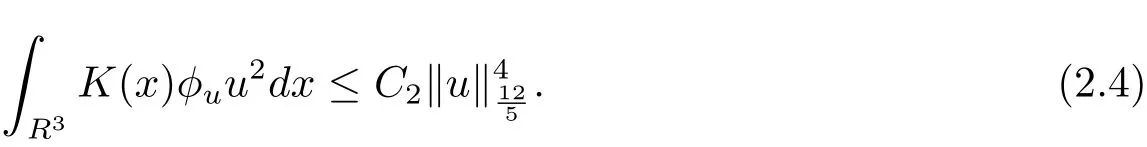


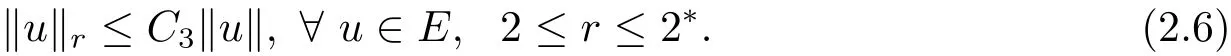
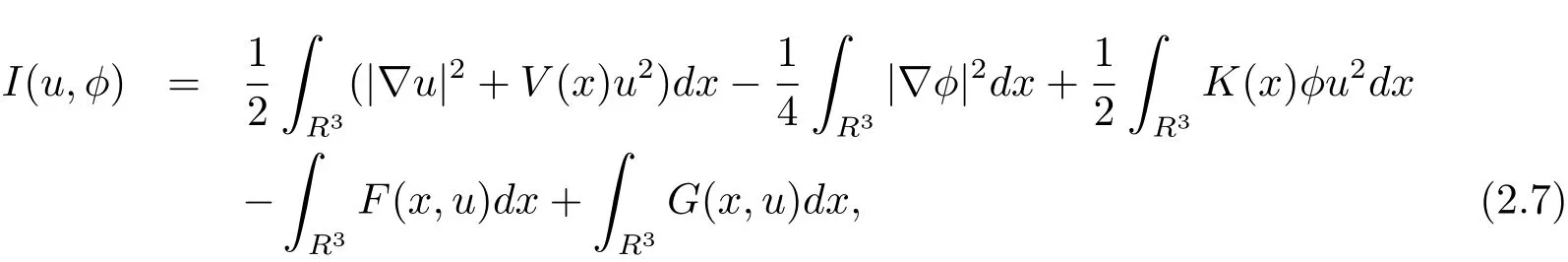

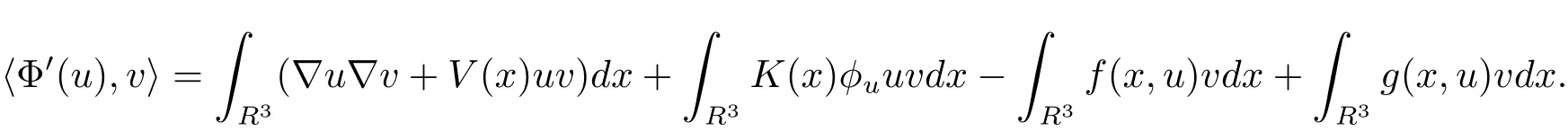

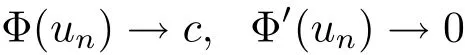
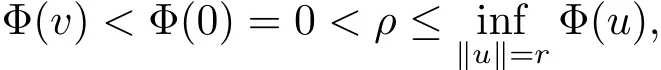
3 定理1.1的证明