CHARACTERIZATION OF A CLASS OF PROPER HOLOMORPHIC MAPS FROM BnTO BN
YANG Bi-tao,YIN Wan-ke
(School of Mathematics and Statistics,Wuhan University,Wuhan 430072,China)
Abstract: The paper is concerned with the study of rational proper holomorphic maps from the unit ball Bnto the unit ball BN.When the geometric rank of the maps are κ0andwe give a characterization of their normalized maps.
Keywords: proper holomorphic maps;holomorphic classi fication;geometric rank;degeneracy rank
1 Introduction
Let Bnbe the unit ball in CN,and denote by Rat(Bn,BN)the collection of all proper holomorphic rational maps from Bnto BN.Let Hn={(z,w)∈Cn−1×C|Im(w)>|z|2}be the Siegel upper half space and denote by Rat(Hn,HN)the collection of all proper holomorphic rational maps from Hnto HN.By the Cayley transform,we can identify Bnwith Hn,and identify Rat(Bn,BN)with Rat(Hn,HN).We say thatf,g∈Rat(Bn,BN)are spherically equivalent(or equivalent,for short)if there areσ∈Aut(Bn)andτ∈Aut(BN)such thatf=τ◦g◦σ.
The study of proper holomorphic maps can date back to the work of Poincar´e[17].Alexander[1]proved that for equal dimensional case,the map must be an automorphism.For the dif f erent dimensional case,by the combining ef f orts of[5,8,19],we know that forN∈(n,2n−1)withn≥2,any mapF∈Rat(Bn,BN)is spherically equivalent to the map(z,0).This is now called the first gap theorem.
For the second gap theorem,Huang-Ji-Xu[11]proved that any mapF∈Rat(Bn,BN)withN∈(2n,3n−3)andn≥4,must equivalent to a map of the form(G,0)withG∈Rat(Bn,B2n).Together with the classification theorems Huang-Ji[10]and Hamada[7],Rat(Bn,B2n)must equivalent to(z,0)or(G1,0)or(G2,0),whereG1∈Rat(Bn,B2n−1)is the Whitney map andG2∈Rat(Bn,B2n)is in the D’Angelo family.
In[12],Huang-Ji-Yin proved the third gap theorem.Namely,when N∈(3n,4n−7)and n≥8,any map F∈Rat(Bn,BN)must be equivalent to a map of the form(G,0)with G∈Rat(Bn,B3n).The classification problem for N=3n−3 is achieved by[2].When N≥3n−2,the map is no longer monomials and can be very complicated.In fact,[6]constructed a family of maps in Rat(Bn,B3n−2),which can not be equivalent to any polynomial maps.Recently,Gul-Ji-Yin[14]gave a characterization of maps in Rat(Bn,B3n−2).The interesting reader can refer to[3,4,9,12,15,16,18]for other related mapping problems between balls.
It seems to be quite less in known for N≥3n−2.The present paper is devoted to a characterization of proper holomorphic maps from Bnto BNwith geometric rank κ0andWe now state our main theorem,with some terminology to be defined in the next section.
Theorem 1.1(1)Let F ∈ Rat(Bn,BN)with the geometric rank of F being κ0andn and F is normalized,then it takes the following form
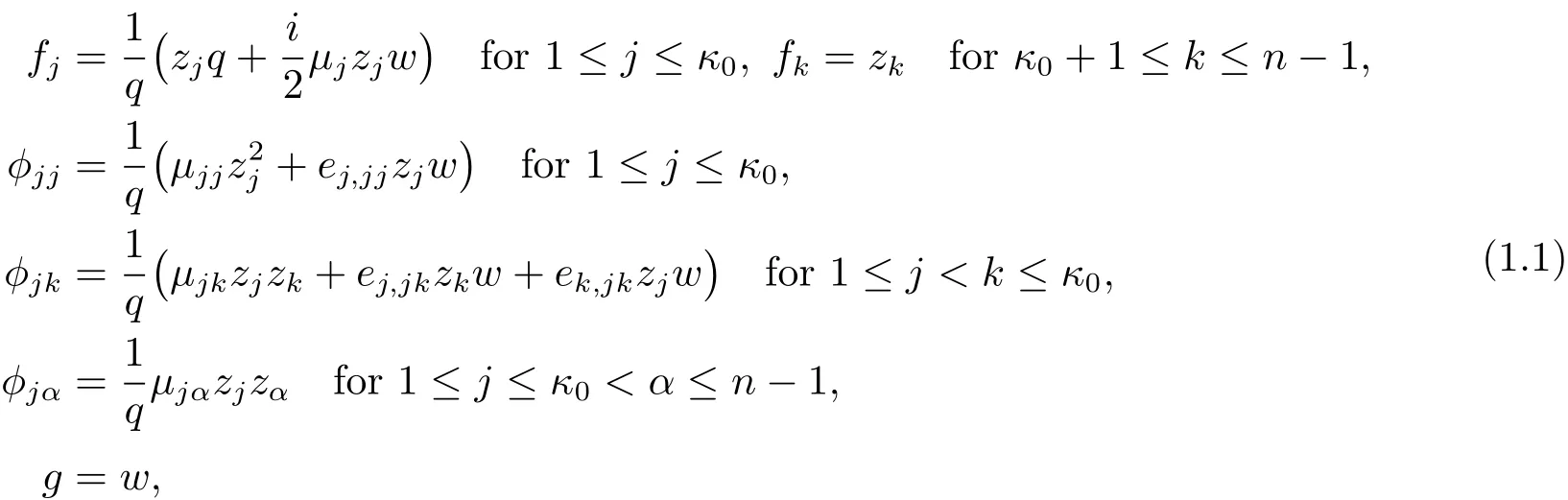
where
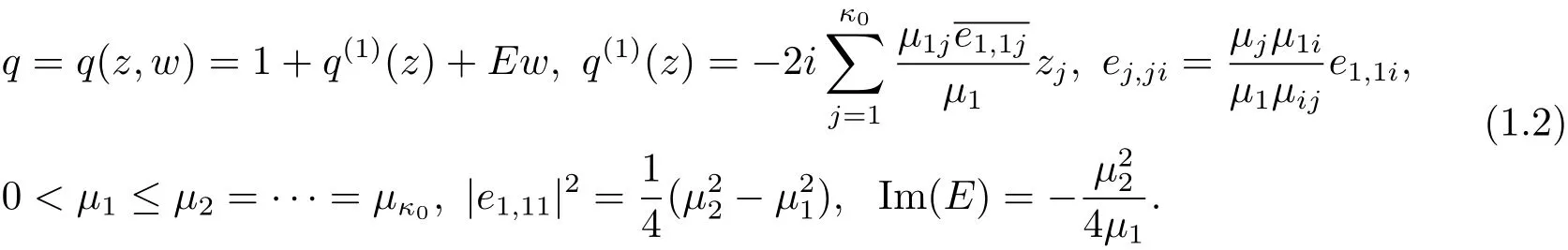
(2)Conversely,if F is defined by(1.1)and(1.2),then the map F is in Rat(Bn,BN)with
2 Preliminaries
Let F=(f,φ,g)=(fe,g)=(f1,···,fn−1,φ1,···,φN−n,g)be a non-constant rational CR map from an open subset M of∂Hninto∂HNwith F(0)=0.For each p∈ Mclose to 0,we write∈ Aut(Hn)for the map sending(z,w)toand writefor the map Then F is equivalent tNotice that F0=F and Fp(0)=0.The following theorem is important for understanding the geometric properties of Prop(Hn,HN).
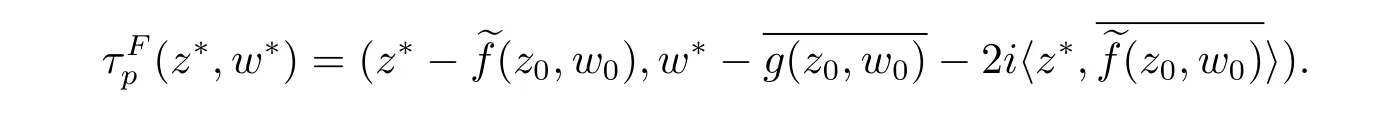
Lemma 2.1Let F∈Prop2(Hn,HN)with 2≤n≤N.For each p∈∂Hn,there is an automorphismsatis fies the following normalization
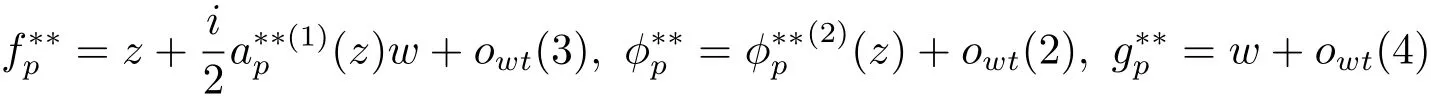
with
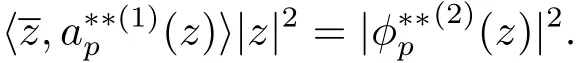
Here we use the notation h(k)(z)to denote a polynomial h which has degree k in z,and a functionis said to be quantity owt(m)if huniformly for(z,u)on any small compact subset of 0 as t(∈ R)→ 0.
Now,we are in a position to the de finition of the geometric rank.Write A(p):=Then the geometric rank of F at pis de fined to be the rank of the(n−1)×(n−1)matrix A(p),which is denoted by RkF(p).Notice that RkF(p)is a lower semi-continuous function on p,it is independent of the choice of τp∗∗(p),and depends only on p and F.De fine the geometric rank of F to beDe fine the geometric rank of F ∈ Prop2(Bn,BN)to be the one for the map
When 1≤κ0≤n−2,a nice normalization was achieved by[9]and[11].
Theorem 2.2Suppose that F∈Prop3(Hn,HN)has geometric rank 1≤κ0≤n−2 with F(0)=0.Then there are σ ∈ Aut(Hn)and τ∈ Aut(HN)such that τ◦F ◦ σ takes the following form,which is still denoted by F=(f,φ,g)for convenience of notation
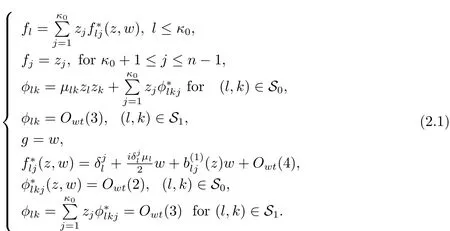
Here,for 1≤ κ0≤ n−2,we write S=S0∪S1,the index set for all components of φ,where
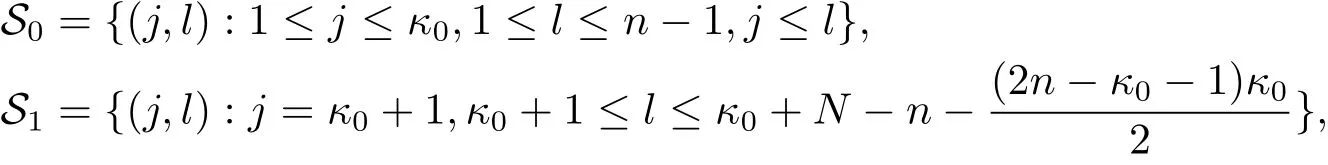
and
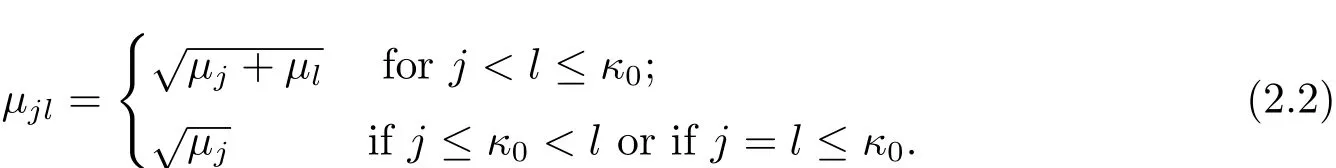
Here we can assume µ1≤ µ2≤ ···≤ µκ0.By[2],we can further assume that
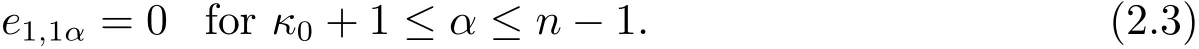
A map F∈Rat(Hn,HN)is called a normalized map if F takes form(2.1)with(2.3).Notice that any F ∈ Rat(Hn,HN)can not be further normalized except some rotations in φlkwith(l,k)∈S1.
Next we introduce some notations that will be use during the proof of our main theorem.Let F=(f,φ,g) ∈ Rat(Bn,BN)be as in Theorem 1.1.Denote bythe number of elements in the set A.Then we haveNotice that=n−1=1,]which means we do not have the S1part in the map.
For any rational holomorphic mapon Cn,where{Pj,Q}are relatively prime holomorphic polynomials,the degree of H is de fined to be
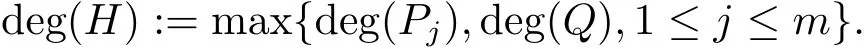
For any holomorphic map P(z,w),we will use the following notations
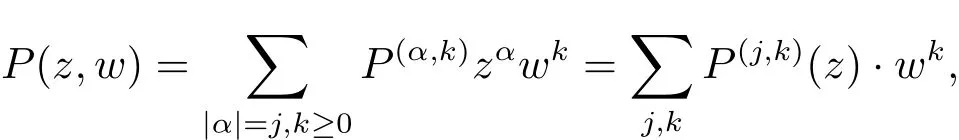
where P(j,k)(z)is a homogeneous polynomial with respect to z of degree j.
2 Proof of the Main Theorem
This section is devoted to the proof of Theorem 1.1.
By[15,Theorem 1.1],we know degF=2.From(4.2)–(4.4)of[15],we obtain
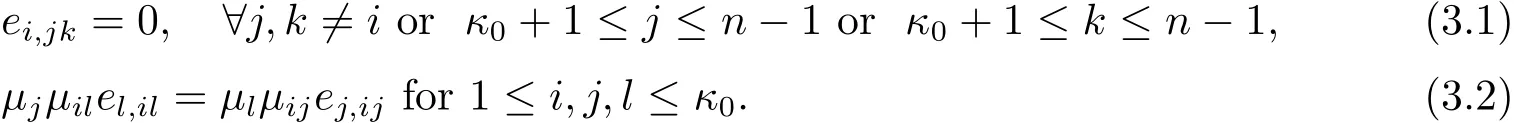
From(5.3)of[15],we get
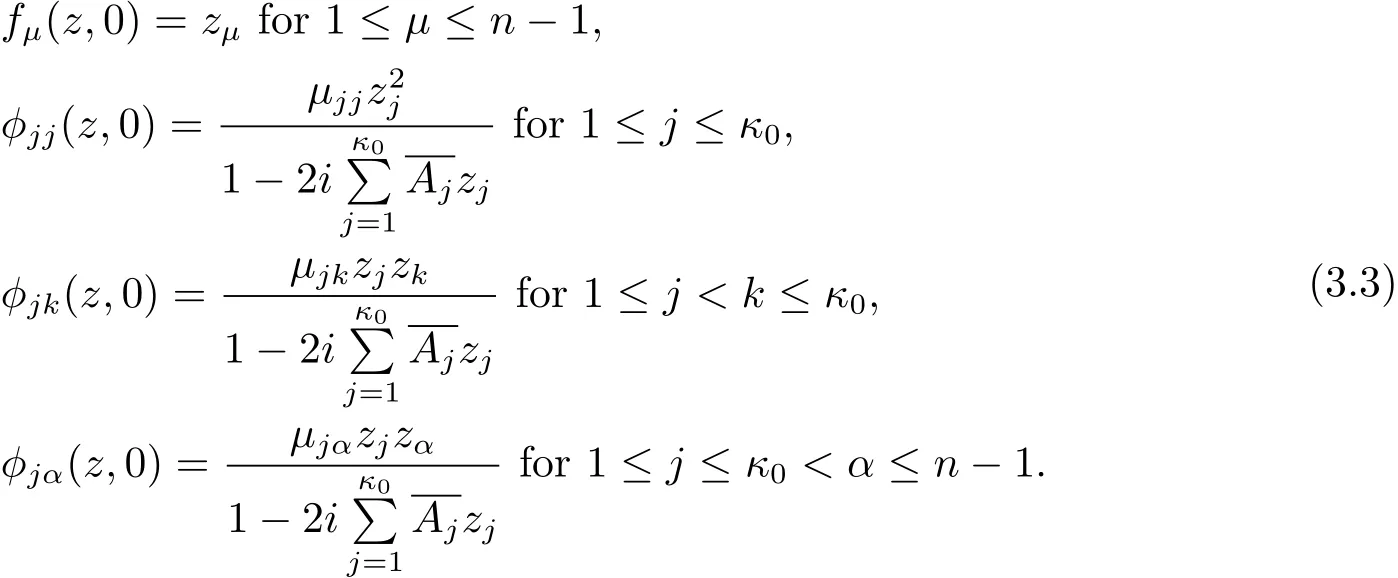
Notice that the degree of F must be 2.Together with the normalization properties in(2.1),the expression of F must have the following form
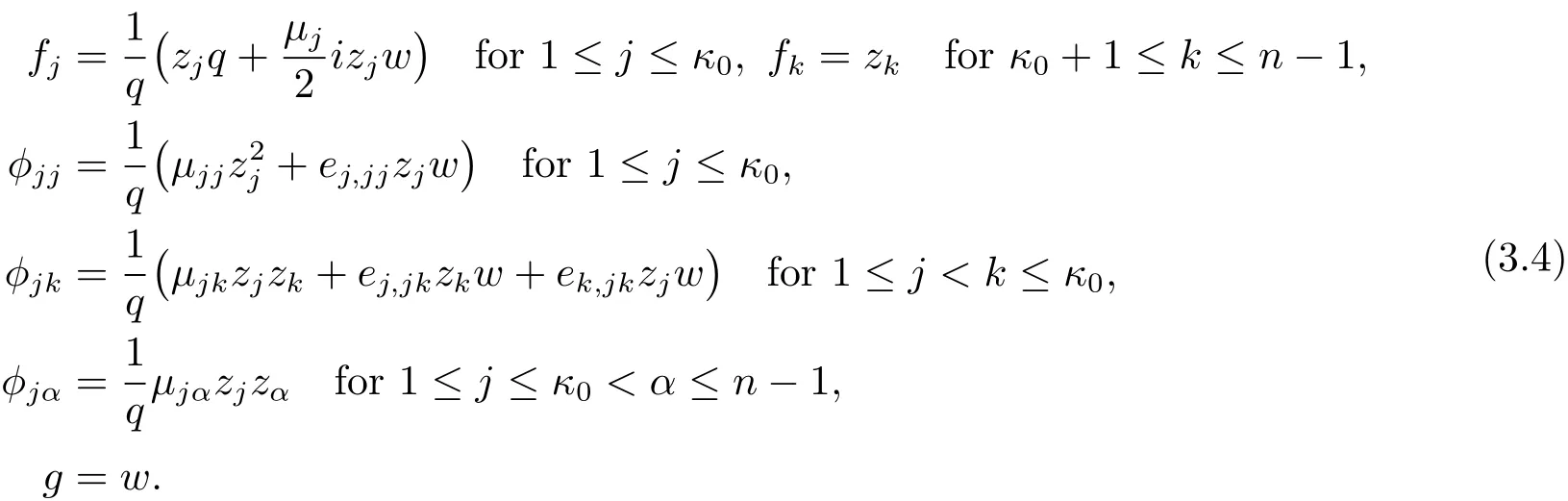
Since F maps∂Bnto ∂BN,we have the basic equation
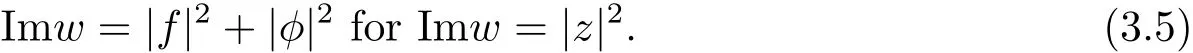
Substituting(3.4)into this equation,we obtain,for Imw=|z|2,the following
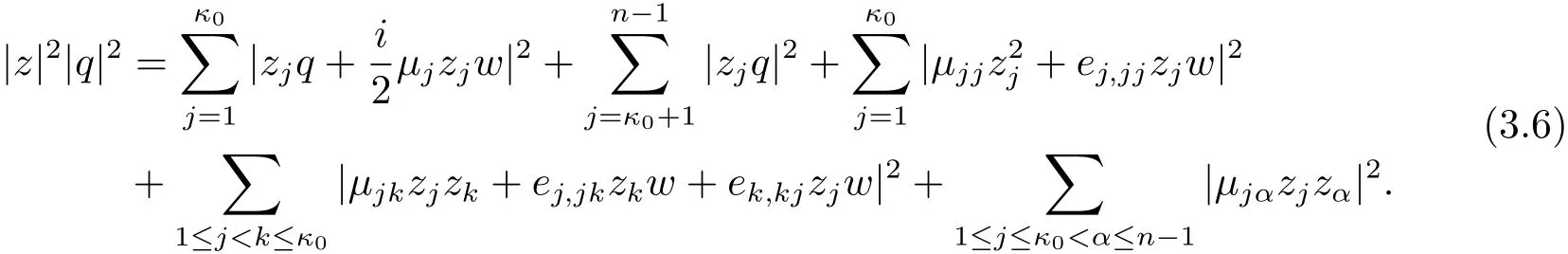
After a quick simplification,we obtain
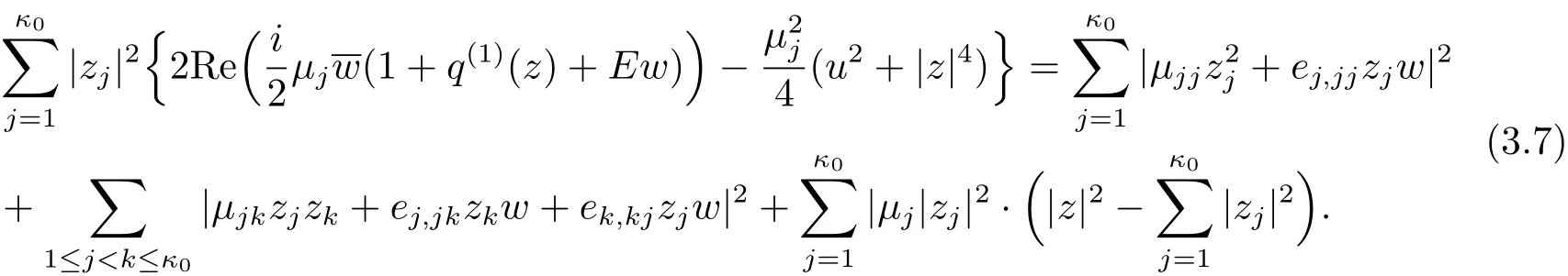
Consideration of the Degree 4 TermsBy considering the degree 4 terms,we get
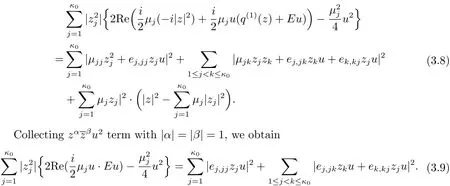
By considering the coefficients ofterms with 1≤ j≤ κ0and zjzku terms with 1≤j Combining this with(3.2),we know only one of e1,1j1≤j≤κ0is non zero.From(3.2)and(3.10),we obtain Together with µ1≤ ···≤ µκ0,we get e1,12= ···=e1,1κ0=0 and µ2= ···= µκ0.Furthermore,we obtain Thus This equation is a trivial formula. We can easily derive from this equation the following These equations were achieved before and we do not get new equations. Consideration of the Degree 5 TermsBy considering the degree 5 terms,we get Deleting|z|2from both sides and consider the termsrespectively,we can easily derive from this equation the following As before,we do not get new equations. Consideration of the Degree 6 TermsBy considering the degree 6 terms,we get Notice that this equation is equivalent to(3.10). In conclusion,the map F must be of form(1.1)with relations in(1.2).The arguments above also showed that this map is indeed a map in Rat(Bn,BN).This completes the proof of Theorem 1.1.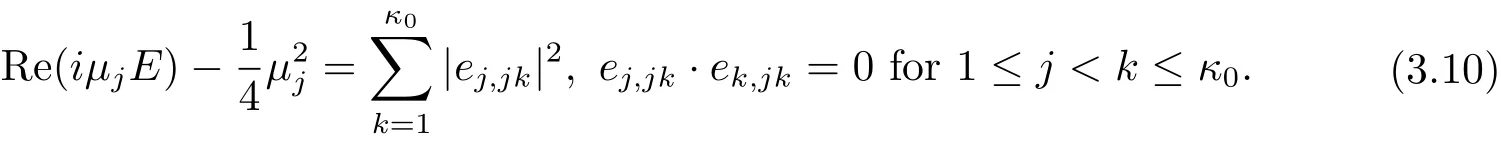
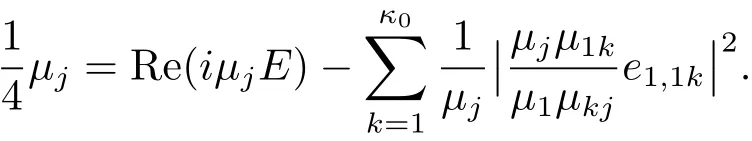
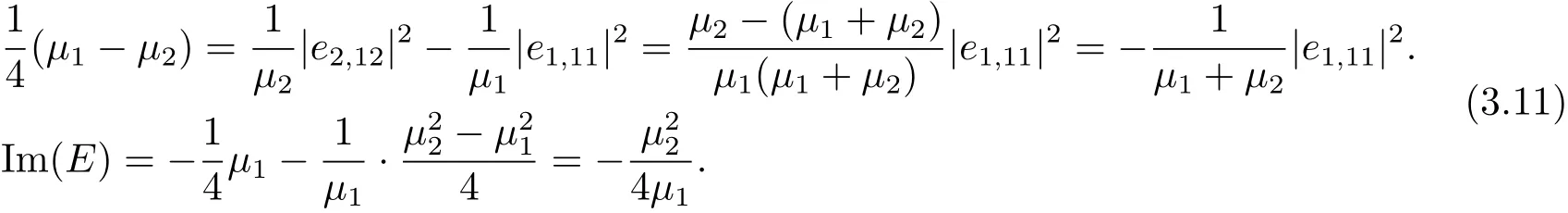
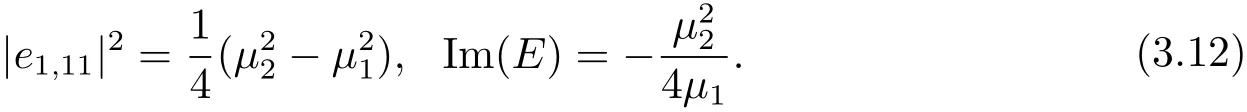
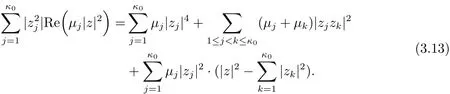
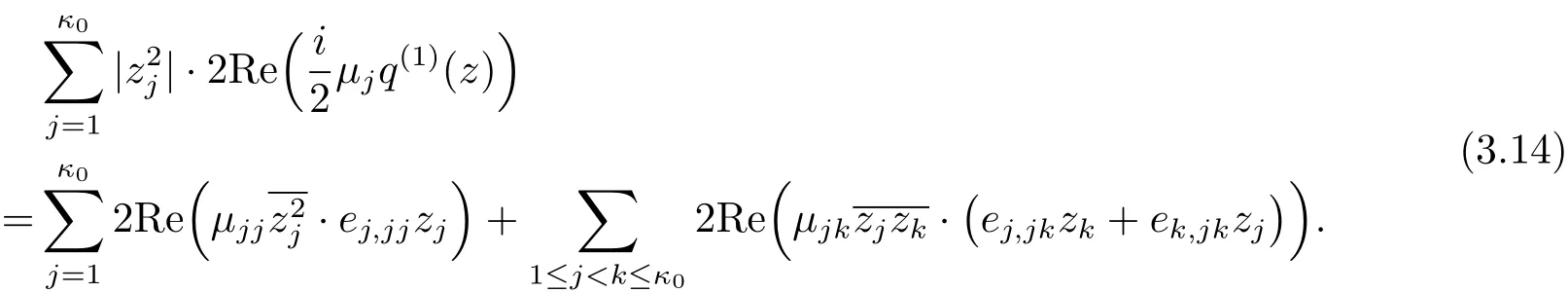
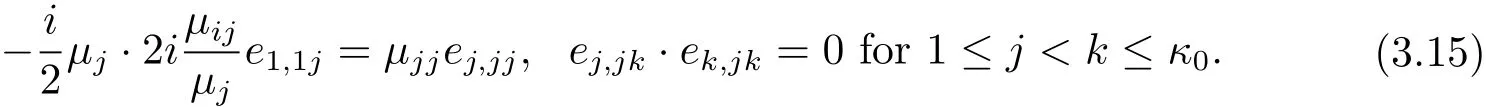
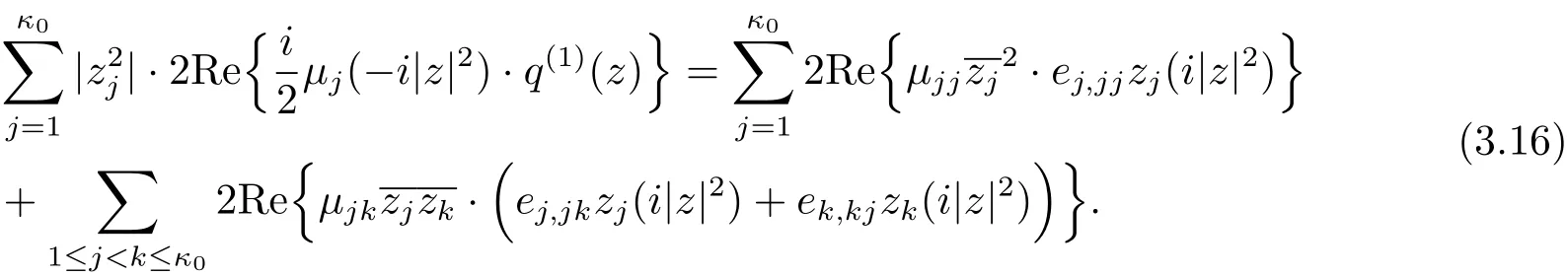
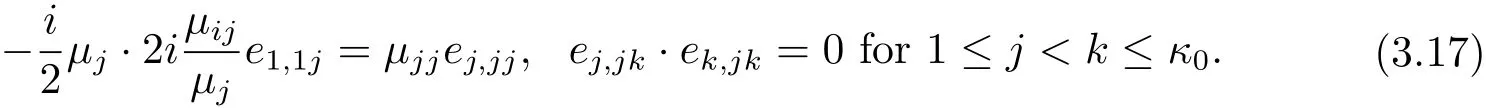
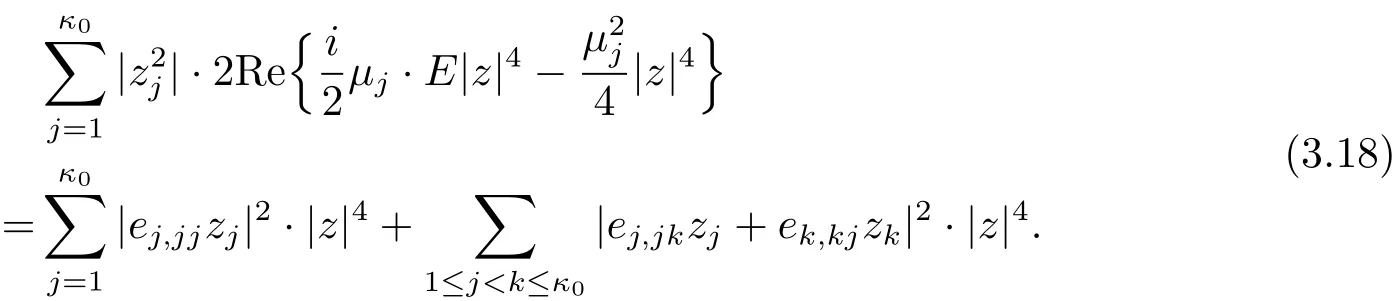
- 数学杂志的其它文章
- TRANSPORTATION INEQUALITIES FOR THE FOURTH-ORDER STOCHASTIC HEAT EQUATIONS WITH FRACTIONAL NOISES
- OPTIMAL CONTROL PROBLEMFOR EXACT SYNCHRONIZATION OF ORDINARY DIFFERENTIAL SYSTEMS
- GRAPHS WITH SMALL NEGATIVE INERTIA INDEX
- 关于短区间的并集中D.H.Lehmer问题的一个推广
- 一维可压缩Navier-Stokes方程组趋向于接触间断波的零耗散极限
- 乘积G-空间的G-极小性、G-混合性和G-链回归点

