GRAPHS WITH SMALL NEGATIVE INERTIA INDEX

MA Hai-cheng,XIE Cheng-ling,LI Dan-yang

(School of Mathematics and Statistics,Qinghai Nationalities University,Xining 810007,China)

Abstract: For a graph G with order n,the number of positive and negative eigenvalues of G,denoted by p(G)and n(G),respectively,are called the positive and negative inertia indices of G.The inertia indices are closely related to the nullity of the graph,which has important applications in chemistry，and is intensively studied,especially for molecular graphs.The main objective of this paper is to determine the structure of graphs with small negative inertia index.By utilizing vertex multiplications,we obtain a characterization for graphs G with n(G)≤2,as well as for graphs G with pendent vertices and with n(G)≤3.

Keywords: positive inertia index;negative inertia index;multiplication of vertices

1 Introduction

We consider finite simple graphs in this paper.Undefined concepts and notations will follow[1],and so we writeG=(V(G),E(G))to denote a simple graph with vertex setV(G)and edge setE(G).As in[1],for a vertex subsetU⊆V(G),G[U]is the subgraph ofGinduced byU.For a vertexu∈V(G),defineNG(u)={v∈V(G)|vis adjacent touinG}to be the neighborhood of vertexuinG,anddG(u)=|NG(u)|as the degree ofuinG.For integersn,n1,···,nt>0,Kn,CnandKn1,n2,···,ntdenote the complete graph onnvertices,then-cycle and the complete multipartite graph,respectively.IfGandHare two vertex disjoint graphs,thenG∪Hdenotes the disjoint union ofGandH.

Throughout this paper,the vertices of a graphGare often labeled asV(G)={v1,v2,···,vn},wheren=|V(G)|.As in[1],the adjacency matrix ofGis ann×nmatrixA(G)=(aij)n×n,whereaijis the number of edges joiningviandvjinG.The eigenvaluesλ1,λ2,λ3,···,λnofA(G)are said to be the eigenvalues of the graphGand to form the spectrum of this graph.The number of positive,negative and zero eigenvalues in the spectrum ofGare called positive inertia index,negative inertia index and nullity of the graphG,and are denoted byp(G),n(G)andη(G),respectively.Obviouslyp(G)+n(G)+η(G)=n.The rank ofG,written asr(G),is the number of nonzero eigenvalues in the spectrum ofG.It follows from the definitions thatr(G)=p(G)+n(G)=n−η(G).

In chemistry,a conjugated hydrocarbon molecule can be modeled by its molecular graph G,where the vertices of G represent the carbon atoms,and the edges of G represent the carbon-carbon bonds of the conjugated molecule.The nullity(as well as the rank)of a molecular graph G has a number of important applications in chemistry.For example,it is known[2]that η(G)=0 is a necessary condition for the molecule represented by G to be chemically stable.More studies on nullity or rank of graphs can be found in[3–28],among others.To the best of our knowledge,very few studies on the positive and negative inertia indices of graphs were conducted.In[29],Hof f man showed that a graph has exactly one negative eigenvalue if and only if its non-isolated vertices form a complete bipartite graph.In[30],Smith showed that a graph has exactly one positive eigenvalue if and only if its non-isolated vertices form a complete multipartite graph.In[31],graph G is characterized with p(G)≥n−2,where n=|V(G)|.It raises the problem of characterizing graph G with small negative inertia indices.

This motivates the current research.In this paper,we present a complete characterization for graphs G with n(G) ≤ 2,and for graphs G with both δ(G)=1 and n(G) ≤ 3,where δ(G)is the smallest degree of G.

This paper is organized as follows:in Section 2,preliminary lemmas will be presented.A Characterization for graph G with n(G)≤2,and for graph G with pendent vertices and with n(G)≤3 are given in Sections 3 and 4.The characterization of graph G with n(G)≤2 extends the former result of Hof f man in[29].

2 Priliminaries

Lemma 2.1Let G and H be graphs.Then

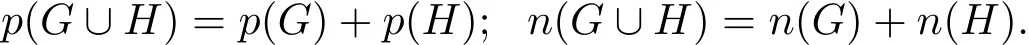
Lemma 2.2(see[30])A graph G has exactly one positive eigenvalue if and only if its non-isolated vertices form a complete multipartite graph.

Lemma 2.3(see[9,32])(the Cauchy inequalities)Let A be Hermtian matrix with eigenvalues λ1≥ λ2≥ ···≥ λn,B be one of its principal submatrices and B have eigenvaluesµ1≥ ···≥ µm.Then the inequalities λn−m+i≤ µi≤ λi(i=1,···,m)hold.

Lemma 2.4Let H be a vertex-induced subgraph of G.Then

(1)r(H)≤r(G),p(H)≤p(G)and n(H)≤n(G).

(2)If r(H)=r(G),then p(H)=p(G)and n(H)=n(G).

ProofLemma 2.4 follows from Lemma 2.3 and from the inequality r(H)=p(H)+n(H)≤p(G)+n(G)=r(G).

Lemma 2.5(see[33])Let G be a connected graph with rank k(≥2).Then there exists a vertex-induced subgraph H(of G)on k vertices such that r(H)=k.

As in[1],a vertex subset I⊆V(G)of a graph G is an independent set(also referred as a stable set)of G if G[I],the subgraph induced by I,is edgeless.Let m=(m1,m2,...,mn)be a vector of positive integers.Denote by G◦m the graph obtained from G by replacing each vertex viof G with an independent set of miverticeand joiningwithif and only if viand vjare adjacent in G(1≤s≤mi,1≤t≤mj).The resulting graph G◦m is said to be obtained from G by multiplication of vertices.

Let Ω be the set of some graphs,we denote by M(Ω)the class of all graphs that can be constructed from one of the graphs in Ω by multiplication of vertices.

Lemma 2.6(see[5,6])Let G and H be graphs.If G∈M({H}),then r(G)=r(H).Furthermore,in this case,we have both p(G)=p(H)and n(G)=n(H).

A graph is called a basic graph if it has no isolated vertex and can not be obtained from other graphs by multiplication of vertices.By definition,a graph with no isolated vertices is not a basic graph if and only if it has two vertices which have same neighborhoods.By Lemma 2.6,it suffices to study basic graphs when we investigate graph invariants such as the rank,the positive inertia index and the negative inertia index.

Lemma 2.7(see[19])Let G be a graph containing a pendant vertex,and let H be the induced subgraph of G obtained by deleting the pendant vertex together with the vertex adjacent to it.Then p(G)=p(H)+1 and n(G)=n(H)+1.

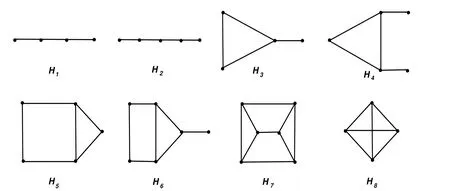
Figure 1:the connected basic graph with r(H)=4

Lemma 2.8(see[5,6,8])Let G be a connected graph.Then

(a)r(G)=2 if and only if G∈M({K2}),

(b)r(G)=3 if and only if G∈M({K3}),

(d)r(G)=5 if and only if G ∈ M(Ω2),where Ω2={G1,G2,···,G24},

where graphs Hi(i=1,2,···,8)are depicted in Figure 1 and graphs Gi(i=1,2,···,24)are depicted in Figure 2.

Lemma 2.9(see[31])Let G be a graph of order n,then p(G)=n−2 if and only if one of the following holds

(1)n=2,G∼=2K1;or

(2)n=3,G∼=K1SK2,K1,2or K3;or

(3)n=4,G∼=F1,F2or F3;or

where graphs Fi(i=1,2,3)are depicted in Figure 3.

“Good evening.” The waiter said. “ Table for four?”“Yes, thank you.”“Smoking or non?”“Nonsmoking.”“Would you prefer to dine indoors or outdoors this evening?”“I guess indoors would be good.”

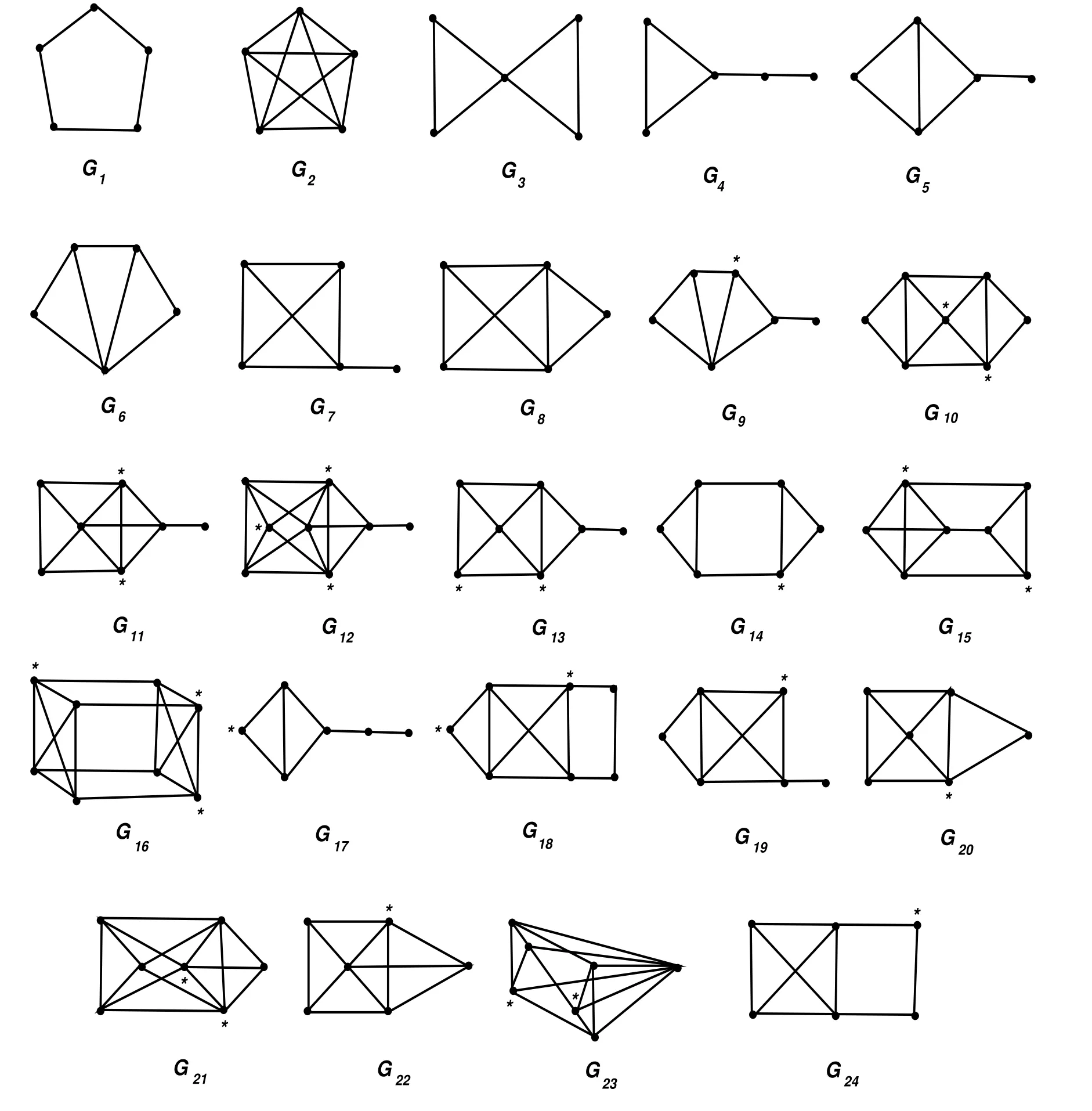
Figure 2:the connected basic graph with r(G)=5

3 Characterization of Graphs G with n(G)≤2

The following lemmas will be needed in our characterization.

Lemma 3.1(see[29])A graph has exactly one negative eigenvalue if and only if its non-isolated vertices form a complete bipartite graph.In other words,if G is a connected

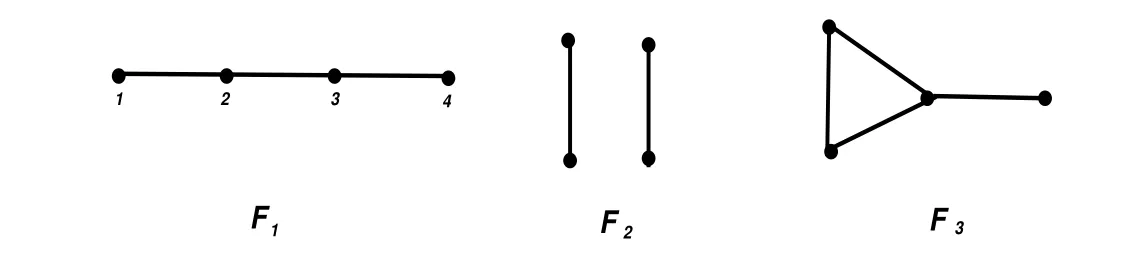
Figure 3:The graph G with four vertices and p(G)=2

graph,then n(G)=1 if and only if G∈M({K2}).

Lemma 3.2Let G be a connected graph.Then n(G)=2 if and only if G ∈ M(Ω3),where Ω3={K3,C5,H1,H2, ···,H7},and the graphs Hi(i=1,2,···,7)are defined in Figure 1.

ProofIt is routine to verify that n(G)=2 for G∈{K3,C5}∪{Hi|1≤i≤7}.Thus the sufficiency follows from Lemma 2.6.

To prove the necessity,we note that r(G)>n(G)=2.If r(G)=3,then by Lemma 2.8(b),G ∈ M({K3}).If r(G)=4,then by Lemma 2.8(c),G ∈ M({H1,H2,···,H8}).However,as direct computation yields n(H8)=3,we must have G ∈ M({H1,H2,···,H7}).

If r(G)=5,then by Lemma 2.8(d),G ∈ M({G1,G2,···,G24}).Direct computation yields n(G2)=4.To determine the values of the other n(Gi)’s,we utilize Table 1 of[9]to findBy deleting the vertices which be marked∗in graphs depicted in Figure 2,we observe that each Gi,9≤i≤18,has a vertex-induced subgraph isomorphic to G4,that each of G19,G20and G21has a vertex-induced subgraph isomorphic to G5,that each of G22and G23has a vertex-induced subgraph isomorphic to G6,and that G24has a vertex-induced subgraph isomorphic to G7.It follows by Lemma 2.4(2)that n(Gi)=3,9≤i≤24.Hence in this case,G∈M({G1})=M({C5}).

If r(G)=k≥6,then by Lemma 2.5,there exists a vertex-induced subgraph H(of G)on k vertices such that r(H)=k.Furthermore,by Lemma 2.4(2),we have n(H)=2 and p(H)=k−2.However,there does not exist such a graph H by Lemma 2.9.This means that there does not exist graph G with r(G)=k≥6 and n(G)=2.

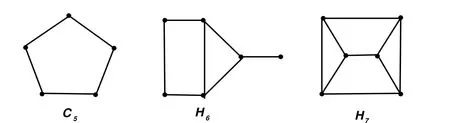
Figure 4:basic extremal graphs with respect to n(G)=2.

A graph G is called basic extremal graph with respect to n(G)=2,if G is a basic graph with n(G)=2,and G is not a proper vertex-induced subgraph of any other basic graphs H with n(H)=2.By definition,since K3is a proper vertex-induced subgraph of H6,hence K3is not a basic extremal graph with respect to n(G)=2,the same graphs Hi(i=1,2,3,4,5)are not basic extremal graph with respect to n(G)=2.However,it is routine to verify that the graphs G in Figure 4 are basic extremal graphs with respect to n(G)=2.

Theorem 3.1 now follows from Lemma 3.1 and Lemma 3.2.

Theorem 3.1Let G be a graph.Then n(G)≤ 2 if and only if G ∈ M(Ω4),where Ω4is the set of all vertex-induced subgraph of each graph in Θ1={C5∪K1,H6∪K1,H7∪K1},and C5,H6,H7are depicted in Figure 4.

4 Characterization of Graphs G with Pendent Vertices and n(G)≤3

Let H be a graph with V(H)={v1,v2,···,vn}and m=(m1,m2,...,mn)be a vector with mi=1 or 2,(i=1,2,···,n).Then V(H)can be divided into two sets:V1={vi∈V(H)|mi=1}and V2={vi∈V(H)|mi=2}.Let v1iand v2ibe the vertices in H◦m by multiplying the vertex viin H when mi=2.For a subset U⊆V1,we construct a graph(H◦m)Uas follows

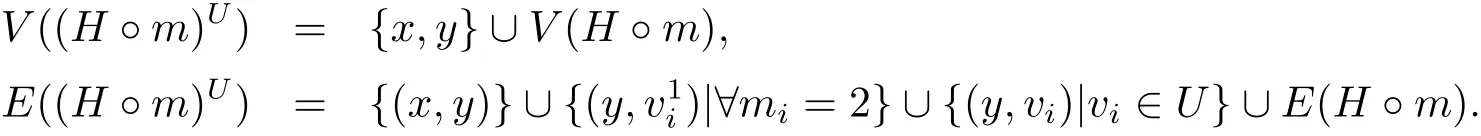
By the definition,(H◦m)Uhas a pendent vertex x.

Lemma 4.1If H is a basic graph,then(H◦m)Uis also a basic graph.

ProofFor any i,j ∈ {1,2,···,n},ifi6=j,as H is a basic graph,then NH(vi)6=NH(vj).So N(H◦m)U(vsi)6=N(H◦m)U(vtj)(1≤ s≤ mi,1≤ t≤ mj).If i=j and mi=2,by the construction of the graph(H◦m)U,we have y∈N(H◦m)U(v1i)and y/∈N(H◦m)U(v2i);x∈N(H◦m)U(y)and x/∈N(H◦m)U(v)for all v(6=y)∈V((H◦m)U);N(H◦m)U(x)={y}and N(H◦m)U(v)6={y}for all v(6=x)∈ V((H ◦m)U)(this is because H has no isolated vertex).In a word,any two vertices in(H ◦ m)Udon’t have the same neighborhoods.Therefore,(H◦m)Uis a basic graph.This proves the lemma.

Let Γ(H)={((H ◦m)U|U ∈ V1,m=(m1,m2,···,mn),mi=1 or 2}be the collection of all graphs(H◦m)U.For the convenience of drawing,when mi=2,we use a hollow circle to indicate two vertices v1iand v2i,which have the same neighborhoods in H◦m,the vertex y is adjacent to v1iand not adjacent to v2i,and we use a black dot to indicate exactly one vertex.For example,the graph(H◦m)Uis depicted in Figure 6,where H=C5,V(H)={v1,v2,v3,v4,v5},m=(2,2,1,1,1)and U={v3,v4}.

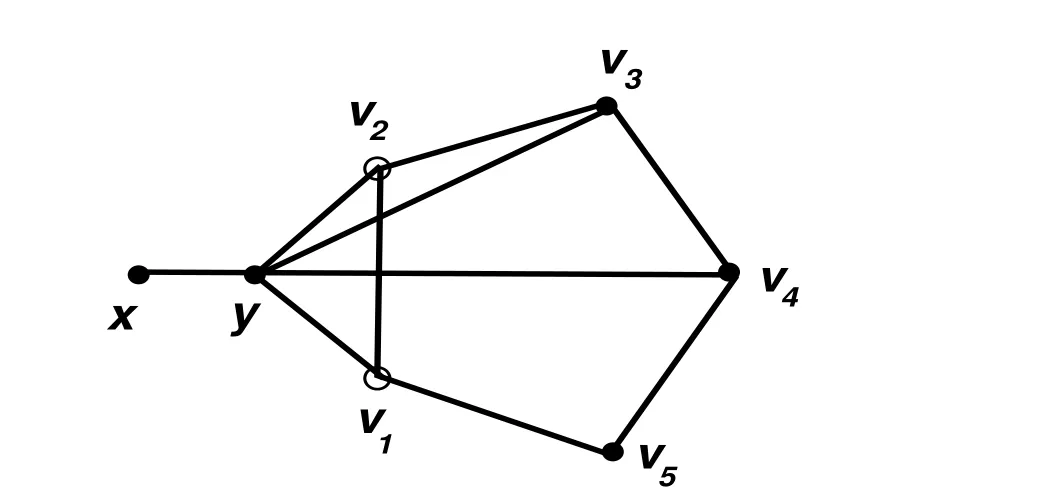
Figure 5:the graph(C5◦m)Uwhere m=(2,2,1,1,1),U={v3,v4}

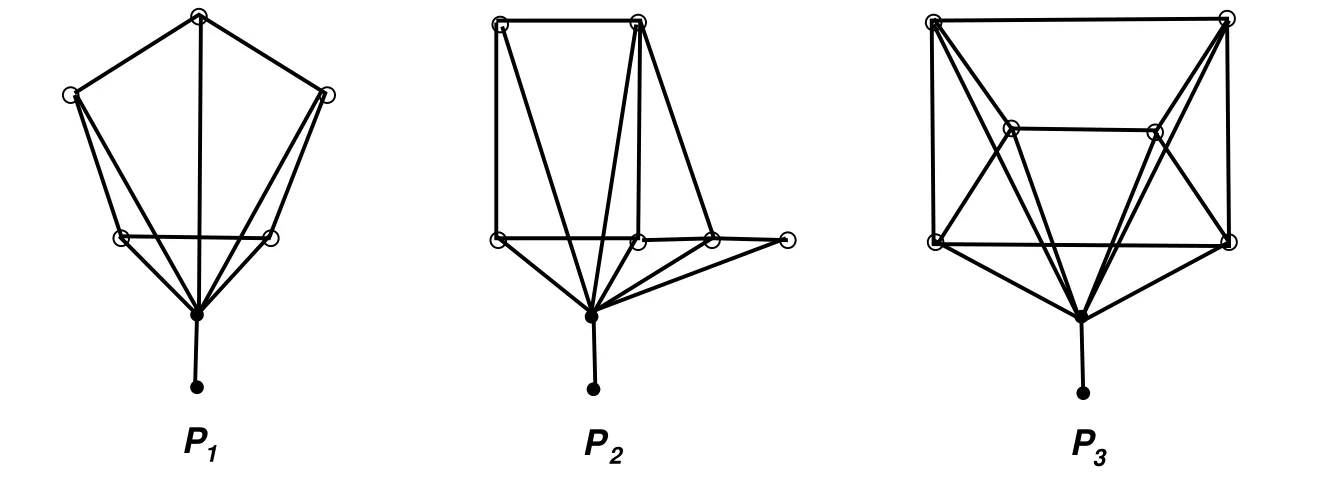
Figure 6:The graphs P1=(C5 ◦ m1)∅,P2=(H6 ◦ m2)∅,P3=(H7 ◦ m2)∅.

Lemma 4.2Let G be a connected graph with pendent vertices and n(G)=3.Then G ∈ M(Ω5),where Ω5= Γ(2K2)∪Γ(K3)∪Γ(C5)∪S7i=1Γ(Hi)and Hi(i=1,2,···,7)are depicted in Figure 1.

ProofWithout loss of generality,assume that G is a basic graph.Let H be the induced subgraph of G obtained by deleting the pendant vertex x together with the vertex y adjacent to it.By Lemma 2.7,we have n(H)=2.Furthermore,H does not have isolated vertices(if not,then the G contains at least an isolated vertex or two pendant vertices all adjacent to y,so G is not a connected graph,or G is not a basic graph,a contradiction).If the graph H is not connected,then by Lemma 3.1,H∈M({2K2}).If the graph H is connected,then by Lemma 3.2,H ∈ M({K3,C5,H1,H2,···,H7}),where graphs Hi(i=1,2,···,7)are depicted in Figure 1.We present the proof for the case when H=K3◦m,where m=(m1,m2,···,mn)be a vector of positive integers,as the proofs for other cases are similar and will be omitted.If mi≥ 3,then there exist s,t ∈ {1,2,···,mi}such that NG(vsi)=NG(vti).If mi=2,v1iand v2iare all adjacent to y or none is adjacent to y,then NG(v1i)=NG(v2i).However,G is a basic graph,this is a contradiction.So mi≤2,furthermore,one and only one of the two vertices v1iand v2iis adjacent to y when mi=2.Therefore,we conclude that G∈Γ(2K2)∪Γ(K3)∪Γ(C5)∪S7i=1Γ(Hi).

For vectors m1=(2,2,2,2,2)and m2=(2,2,2,2,2,2),define P1=(C5◦ m1)∅,P2=(H6◦ m2)∅,P3=(H7◦ m2)∅,as depicted in Figure 6.If

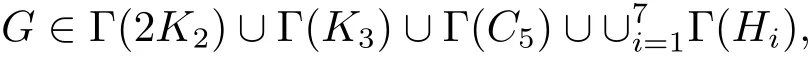
it is straightforward to verity that graphs G are a vertex-induced subgraph of P1,P2,or P3.Hence Theorem 4.1 below follows from Lemma 4.2.

Theorem 4.1Let G be a graph with pendent vertices and n(G)≤3.Then G∈M(Ω6),where Ω6is the set of all vertex-induced subgraph of each graph in Θ2={P1∪K1,P2∪K1,P3∪K1},where Pi(i=1,2,3)are depicted in Figure 6.