善抓要点提思维 活化方法升素养——浅议《数学归纳法》的教学

☉江苏省金湖中学 陈万斌

数学素养是指学生通过数学知识和方法的积累与掌握、运用与内化，在实际情境中经历从数学的角度思考问题，用数学思想分析问题，用数学方法解决问题，进而形成的能力、习惯和品质等.数学核心素养是指数学学习者应具备的适应终身发展和社会发展需要的必备的数学品格和数学关键能力，是学生学习数学所应达成的有特定意义的一种综合性能力，应当在教与学的过程中引起教师与学生的关注.数学核心素养是以数学知识与技能为基础，以运用数学知识与技能解决问题为表现形式，数学本质的把握与相关的数学思想是在数学学习的过程中形成的.而通过对数学归纳法这一内容的学习，就能极大的提高思维能力，从而提升数学素养.

数学归纳法是高中阶段的一种重要的证明方法，用来解决与自然数“n”有关的问题，有着其他证明方法不可替代的作用.学会数学归纳法，不仅要解决相关的数学问题，还要通过解决问题，来深化对数学归纳法内涵的理解，不是套用两个机械的步骤，而是充分利用“有限”的手段来解决“无限”的问题；掌握运用数学归纳法解题的基本要点和注意事项；加深数学归纳法与其他知识和方法的联系，从而提高解决问题的综合能力；同时会灵活运用数学归纳法，不能固化；更重要的是通过对数学归纳法的学习和运用，强化数学归纳法的数学本质，培养学生的逻辑思维能力，提高学生善于联系、擅长逻辑推理的核心素养.

一、掌握归纳法要点

（一）注意两个步骤

1.确定初始值n0

例题1比较2n与n2的大小并证明.

解析：当n=1时，2n＞n2，当n=2时，2n=n2，当n=3时，2n＜n2，当n=4时，2n=n2.

猜测：当n≥5时，2n＞n2.

证明：（1）当n=5时，25＞52，不等式成立.

（2）假设当n=k（k≥5）时，不等式成立，即2k＞k2.

则当n=k+1时，2k+1=2·2k＞2·k2. 因为2k2-（k+1）2=k2-2k-1=k（k-2）-1＞0，

所以2k+1＞（k+1）2，故不等式也成立.

所以由（1）（2）可知：当n≥5时，2n＞n2.

评议：从数值比较中确定初始值，进而找到数学归纳法“递推的基础”.

2.观察“项”的变化

评议：从“n=k”到“n=k+1”时要注意差异性，即“项”的变化，进而推导出数学归纳法“递推的根据”.

3.探寻两步骤联系

（1）寻找递推的关系

例题3…（1+nx）（其中n∈N*且n≥2），其展开后含xr项的系数为

（2）设a2=h（n），a1=g（n），求证：h（n）

解析：（1）易知：a1=1+2+…

h（n+1）=h（n）+（n+1）g（n）.

证明：①当n=2时，a2=2，而h（2）=

所以等式成立.

由①②可知：等式得证.

评议：第二步的“假设”本身就是一个“证明”.

（2）寻觅数式结合的桥梁

例题4已知数列{an}满足的通项公式，并证明.

解析：可以利用特殊值运算后猜测an=2n.

证明：①当n=1，a1=1+1=2，猜想成立.

②假设当n=k时，猜想成立，即ak=2k.

所以ak+1=2ak=2×2k=2k+1，所以当n=k+1时等式也成立.

由①②知：an=2n，n∈N*.

评议：抓住“假设”对数式进行“分解与组合”.

（3）寻求内在的规律

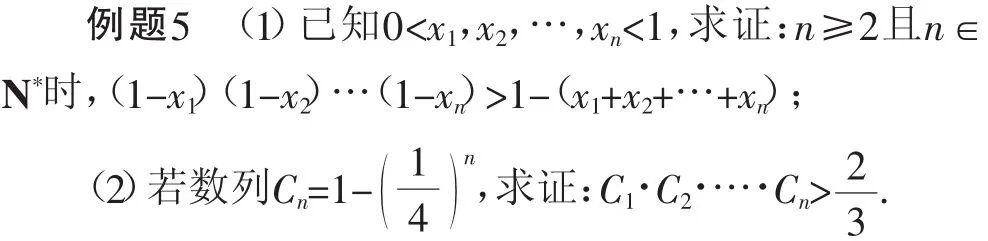
证明：（1）①当n=2时，因为0＜x1，x2＜1，则（1-x1）（1-

②假设n=k（k≥2）时，结论成立.

由①的“证明规律”可知：

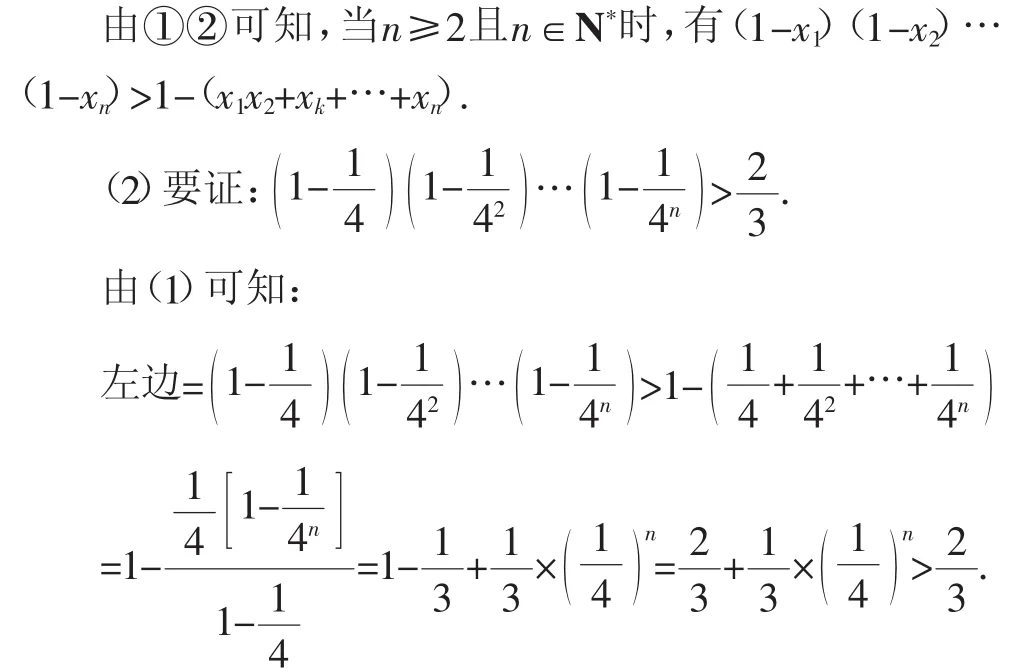
所以原题得证.

评议：通过第（1）问的证明发现内在隐含的关系或规律，再将其用于第（2）问.

（二）注意二次证明

例题6求证（3n+1）·7n-1能被9整除（n∈N*）.

解析：预备证明7n+2能被3整除（数学归纳法证明，证明略）.

本题证明：设Dn=（3n+1）·7n-1，

（1）当n=1时，D1=4×7-1=27=3×9，结论成立.

（2）假设n=k时，结论成立.

即Dk=（3k+1）·7k-1是9的倍数，

则当n=k+1时，

由假设及预备证明可知Dk+1＝7ak+3（7k+1+2）也是9的倍数，所以结论也成立.

由（1）（2）知：对∀n∈N*，（3n+1）·7n-1能被9整除.

评议：有时需要二次证明，即“预备”证明.

二、学会归纳法拓展

例题7已知x+x-1=2cosθ，求证：xn+x-n=2cosnθ（n∈N*）.

证明：（1）当n=1时，等式成立.

当n=2时，x2+x-2=（x+x-1）2-2=（2cosθ）2-2=2cos2θ，所以等式成立.

（2）假设当n≤k时，等式成立.

即xk+x-k=2coskθ，xk-1+x-（k-1）=2cos（k-1）θ，

所以由（1）（2）可知：xn+x-n=2cosnθ.

评议：对数学归纳法的拓展，俗称“第二数学归纳法”.

三、开展多角度联想

（一）与函数有关

例题8对任意x＞1，n∈N*，求证

证明：（1）当n=1时，只需证ex-1＞x.设F（x）=ex-1-x（x＞1），则F（1）=0.又x＞1时，F ′（x）=ex-1-1＞0，所以F（x）是（1，+∞）上的增函数.故当x＞1时，即有F（x）＞0，则ex-1＞x结论成立.

由（1）（2）可知：原题得证.

评议：建构函数，利用函数本身的性质.

（二）与二项展开式有关

例题9已知n≥2且n∈N*，比较（n+1）n与2n·n！的大小.

证明：（1）当n=2时，a2＞b2，不等式成立.

（2）假设当n=k（k≥2）时，不等式成立，ak＞bk，即

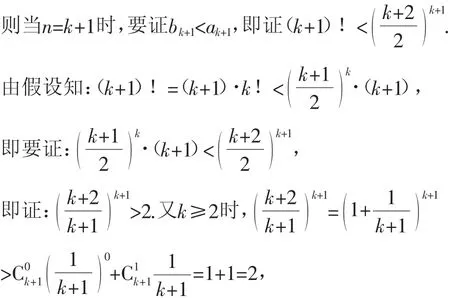
所以bk+1＜ak+1，则不等式也成立.

由（1）（2）可知：当n≥2且n∈N*时，（n+1）n＞2n·n！.

评议：掌握证明过程中的知识交汇、方法交叉和交融.

数学归纳法虽然只有两个步骤，只是解决与自然数“n”有关的命题，看似形式简单、步骤机械、应用面狭窄，其实不然.其一数学归纳法本身格式严谨、内涵丰富，理解数学归纳法需要感悟并深化其本质；另外数学归纳法的步骤二本身就是一个“证明”，要求学生善于运用“假设”；其二数学归纳法应用广泛，方法独特；其三数学归纳法与其他知识、方法联系密切，知识和方法的交叉能极大地提高学生的想象能力，培养学生的发散思维.通过教师的积极引导、学生的反思，不仅使学生掌握数学归纳法的基本步骤、基本要领、基本应用，而且能进行灵活地运用，特别是学会分析问题并能解决问题，更重要的是在学习过程中提高了学生的逻辑推理能力和善于联想的意识，数学素养也因此得到了很大的提高，这才是学习数学知识的最终目的.W