主成分分析在投资组合收益中的应用——以地产股为例

蒋心怡

（苏州大学数学科学学院，江苏 苏州 215006）

一、导论

主成分分析法可用来分析高度相关的变量，它的主要思想是把多个指标转化为综合指标，使这些主成分可以反映变量的绝大部分信息，是一种有效的降维方法。已有不少学者利用此方法对相关变量进行了研究。岳田利、彭帮柱等用主成分方法建立了分析苹果酒香气的评价模型，为评价果酒香气开辟了一条客观的新途径[1]。程鸿群、邹敏通过时序全局主成分分析法建立了中西部房地产投资环境评价指标体系，并用湖北省数据进行了实证研究[2]。彭丽将稀疏主成分分析用于股票投资组合的研究中，验证了稀疏主成分分析的有效性[3]。林海明、杜子芳提出了主成分分析综合评价的应用条件，使评价结果更具合理性[4]。刘遵雄、唐顺发基于主成分分析，研究了均值—熵指数在投资组合风险分散中的应用，为投资者的分散投资提供了有效的权衡[5]。

股票投资组合是投资者把资金按一定比例分别投资于不同股票的一种方案，当组合中比例确定后，需要考虑各只股票的收益率对投资组合整体收益的影响。因股票数量较多，采用主成分分析方法可以有效地减少维数，以较少的主成分反映绝大部分信息。

以上研究并未考虑用主成分方法研究投资组合的收益敏感度，为了弥补此不足，本文选定股票收益率作为研究对象，将主成分分析方法应用于代表性股票收益率的时间序列，求解投资组合收益敏感度。

二、投资组合收益的主成分分析方法

主成分分析方法是一种统计分析方法，将多个指标化为少数几个不相关的综合指标 (所谓主成分) , 笔者将投资组合收益的主成分分析方法叙述如下:

假定一个投资组合由p个资产构成, 它们的收益率分别为xi（i=1,2,…,p）。构造收益率影响的主成分，首先是通过对这p个资产收益率相关性的研究，构造p个不相关的综合指标yi（i=1,2,…,p）,其中每一yi都被合理地表示为各原始收益率的线性组合，这样统计数据所反映的信息就不再有重叠；接着，在上述p个综合指标中选取较少的m (m＜p) 个综合指标, 这m个综合指标能反映出原指标所提供的绝大部分信息,简化了影响因素，从而最终简便求解对整体资产组合收益的影响。

方法的数学原理和公式推导可参考文献[6], 具体步骤如下:

（一）将各变量xi标准化，即对同一变量减去其均值再除以标准差，以消除量纲影响。

（二）在标准化数据阵X=(xij)的基础上计算原始收益率相关系数R=(rij),其中。

（四）在已确定的全部p个主成分中合理选择前m个来实现最终的评价分析, 一般用方差贡献率解释主成分jy反映的信息量大小,m的确定以累计方差贡献率达到足够大的值(一般取85%)为原则;

（五）将各资产一个基点收益率变化相对应的交易组合价值变化代入各主成分的表达式中，获得对应于主成分一个基点收益率变化的交易组合价值变化，即组合收益对主成分的敏感度。

三、地产股收益的主成分分析

（一）投资组合的构造

目前中国房地产行业形势复杂，一方面一、二线城市房源需求持续增加，另一方面国家调控加强，倒逼开发商进行自我革新。在此背景下，大型房企强者恒强，龙头企业不论是土地储备还是融资方面，都远超中小房企。因此，本文关注大型上市房企的股价情况，构造投资组合，选择了具有代表性的八支房地产股票，分别是中国恒大、碧桂园、融创中国、中国海外发展、华润置地、龙湖集团、雅居乐、金地商置。

为了研究主成分对投资组合收益率的影响，本文采用市值加权法进行了投资组合的构造。市值加权是一种传统的投资组合构建方式，方法是按市值的占比来分配权重，因此市值高的公司对应的权重就更大，当这些大公司的股票表现良好时，该投资组合的表现也更好。比如标普500指数就是按照市值进行加权计算的。

企业流通市值等于流通股票数与其股价的乘积，以2019年5月2日收盘价为股价，计算得各企业流通市值如表1所示。

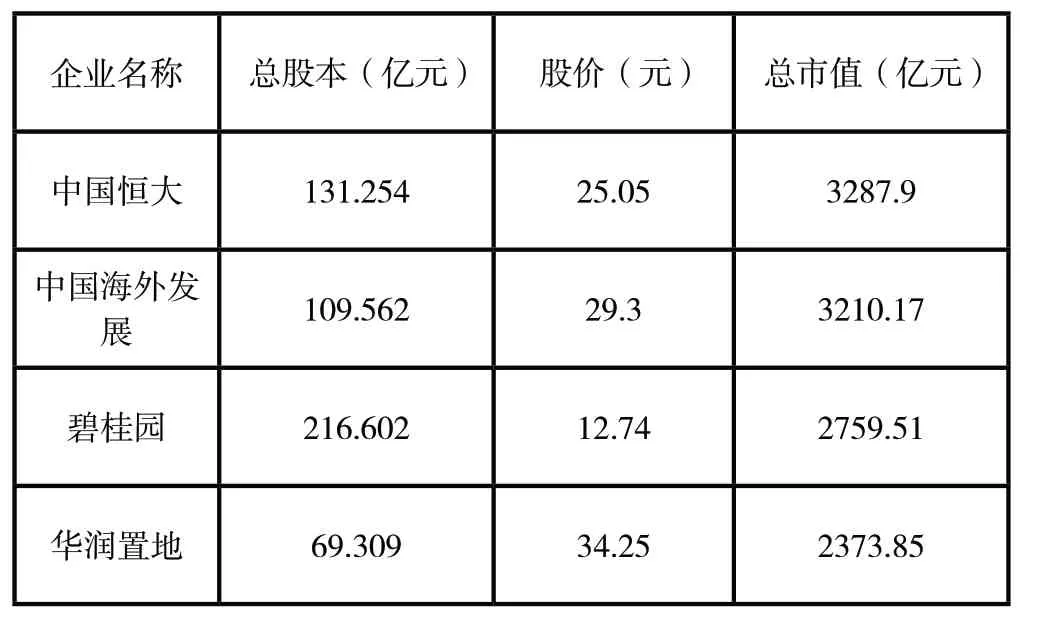
表1 8个房企的流通市值

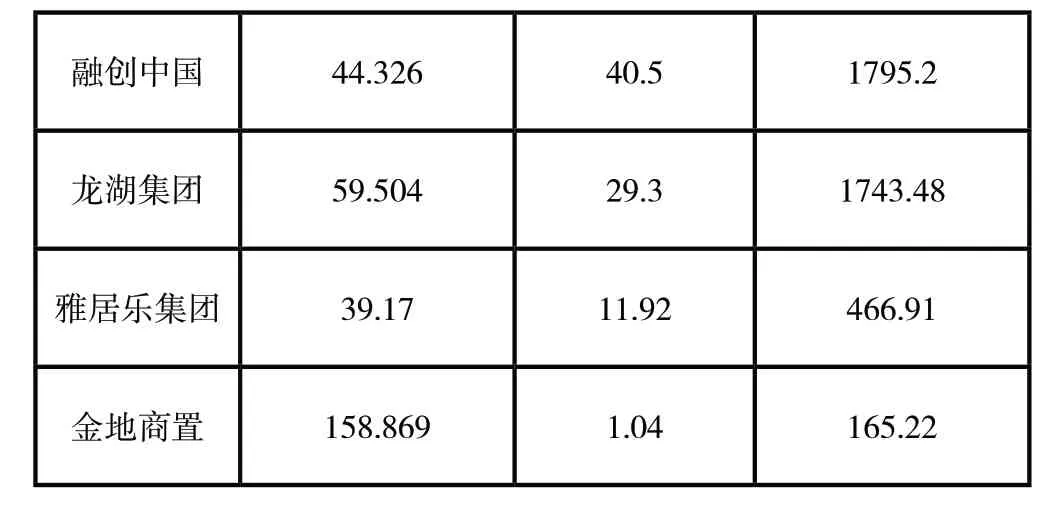
融创中国 44.326 40.5 1795.2龙湖集团 59.504 29.3 1743.48雅居乐集团 39.17 11.92 466.91金地商置 158.869 1.04 165.22

假设总投资金额为100万，以市值加权得到向每个企业的投资金额如表2所示：

表2.各企业投资额

设与第i个房企一个基点收益率变化相对应的交易组合价值变化为εi，第i个房企权重为µi，基点a= 0.01%，投资总额I=1000000，则有，将计算结果列于表3中：

表3. 与一个基点收益率变化相对应的交易组合价值变化（单位：元）

由上表可分析得到，中国恒大收益率变化一个基点会触发组合价值增加量为20.81元，中国海外发展的收益率变化一个基点则会触发组合价值增加20.31元，各房企的收益率与投资组合价值同向变动。

（二）主成分的提取

1、样本矩阵的建立

用choice金融终端软件得到八支房企股票2016年5月到2019年5月间每天的收盘价格。然后对选定的八支房地产股票进行收益率的计算。假定一只股票在第i天的收盘价为iS，定义iu为在第i天连续复利收益率，则有

以中国恒大2016年5月上旬为例，得到的收益率如表4所示：

表4.中国恒大2016年5月上旬收益率

2016年5月至2019年5月间约有739个交易日，将8只股票的收益率看成一个739×8的矩阵，因为收益率在同一量纲上，所以这里不再进行标准化计算。

2、协方差矩阵的建立

要实现一个主成分分析，第一步需要从观测中计算出一个方差-协方差矩阵。协方差矩阵是一个对称阵，对角元为方差，第i行和j列的元素为变量i和j的协方差，协方差越大，说明两者相关性越强。

对于8只股票的收益率矩阵，分别用Excel中的COVARIANCE.S和VAR.S函数计算它们的协方差和方差，用x1～x8表示8只股票的收益率，得到协方差矩阵如表5所示：

表5.收益率的协方差矩阵

从对协方差矩阵的观察可知，碧桂园和融创、恒大和融创、雅居乐和融创的收益率具有一定程度的相关性，金地与其他企业的收益率相关性较弱，由此已对房企收益率之间的关系有了一初步认识。

3、特征值与特征向量的计算

进一步计算协方差矩阵的特征值和特征向量。矩阵的特征向量即因子载荷，它是因子所对应的收益率变动，而矩阵的特征值为因子得分，它是任意一天收益率变化对应某一因子的系数。分别用Excel中编写的Eigenvalues和Eigenvectors函数求得特征值、 特征向量，如表6、表7中所示：

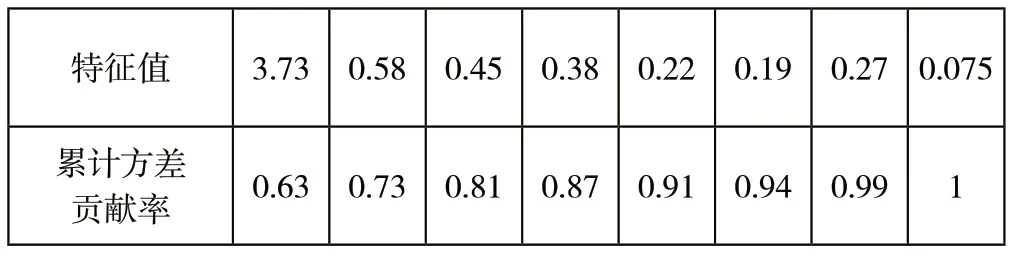
表6.协方差矩阵的特征值

表7.协方差矩阵的特征向量

最高特征值3.73所对应的特征向量PC1为第一主元素，第二高特征值0.58所对应的特征向量PC2为第二主元素，以此类推。由于前四个特征值的累计方差贡献率已达87%，故前四个主成分已反映原始指标所提供的绝大部分信息，可利用它们来对投资组合收益进行研究。

主成分的线性表达式中的原始指标系数在理论上可取对应于特征值的正则化单位特征向量, 而对应于每一特征值的单位特征向量又不是唯一的 (存在符号上的差异) ，本文选取已求得的特征向量作为系数，构造出符合实际的前四个主成分依次为:

由线性表达式中系数的大小及符号, 可对各主成分的实际意义做如下解释:第一主成分为所有八项收益率的综合；第二主成分则与六项收益率成正相关，而与另两项负相关；第三、四主成分又分别较多体现x2、x3的信息。

（三）组合收益的敏感度分析

对于以上构建的投资组合，计算它对四个主成分的敏感度（对于主成分的一个基点变动所触发的变动数量）。

以第一主成分为例，它的一个基点变动对投资组合收益影响为:

同理得到其他三个主成分变动一个单位后，投资组合收益的变动，汇总为下表：

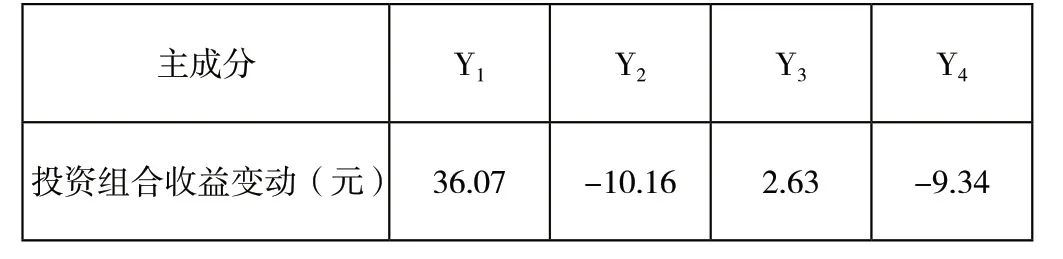
表8.组合收益率对PC1-PC8的敏感度

（四）结果分析及方法的进一步应用

通过对计算结果的分析，本文得到以下结论：

投资组合对主成分的敏感性暴露程度之比等于表5中投资组合收益变动的绝对值之比，所以投资组合对第四个主成分的暴露程度是对于第三个主成分的3.55倍。但是基于表3，第三个主成分的标准差（0.67）是第四个主成分的标准差（0.61）的1.098倍。某主成分对于一个特定的交易组合的重压性可以通过敏感性暴露和因子得分的标准差来衡量[7]，采用这个方法，第二个主成分的重要性是第一个主成分的3.23倍。

主成分分析进一步可应用于检测交易中的特定风险，有如下一些方面：

1、投资组合价值对其中某一资产的敏感性称为Delta，利用主成分分析可以计算其对某一因子的Delta。

2、期权投资组合对于标的资产的两级偏导数称为Gamma，如果直接计算会造成信息超负荷，故可以选择计算交易组合价值对于主成分分析中前两个主要因子的Gamma值。

3、利率产品投资组合的Vega是用来检测交易组合价值对于波动率的暴露程度，与一般检验波动率的方法相比，更简便的是采用主成分分析方法，计算出影响不同产品的波动率变化的主要因子，然后可计算出对应于前两个或三个主要因子的Vega数量。