点几何的解题应用：恒等式篇

彭翕成,张景中,2

(1.华中师范大学 国家数字化学习工程技术研究中心 430079；2. 广州大学计算科技研究院 510006)

寻找一个通法来解决千变万化的几何题，这是很多数学家都思考过的问题.数学家笛卡尔曾对此提出了一个宏伟的设想：先将任何类型的问题化归为数学问题，然后将任何类型的数学问题化归为代数问题，最后将任何代数问题化归为单个方程的求解.此称为笛卡尔之梦.

现在看来，笛卡尔的这一想法过于美好.任一问题转化为数学问题，显得“野心”太大，有点异想天开.在笛卡尔时代，微积分尚未建立，笛卡尔自然不知道微分方程这样的“高端”方程，但即便是多项式方程，求解也并不容易.

后来的数学家给予了笛卡尔之梦很高的评价.如数学家波利亚曾这样评价[1]：笛卡尔的计划失败了，但它仍不失为一个伟大的计划，而且即使失败了，它对数学的影响也超过了偶尔获得成功的千万个小计划.尽管笛卡尔的方案不是对所有的情形都可行，但是它对无穷多种情形行之有效，其中包括无穷多种重要的情形.

也有数学家在尽可能大的范围内去实现笛卡尔之梦.如吴文俊院士认为[2]，笛卡尔提供了不同于欧几里得模式(即从公理出发按逻辑规则演绎进行,一题一证,没有通用的证明法则)的可能性,给出了一条可用计算来证明几何定理的新思路.多项式方程的研究尽管困难很大，也要想办法攻克，因此提出了一系列原理和方法，其中以吴方法最为著名.

下面以外心定理为例，对比一下欧式方法和吴方法.

例1求证三角形的三边的垂直平分线交于一点，该点叫做三角形的外心.

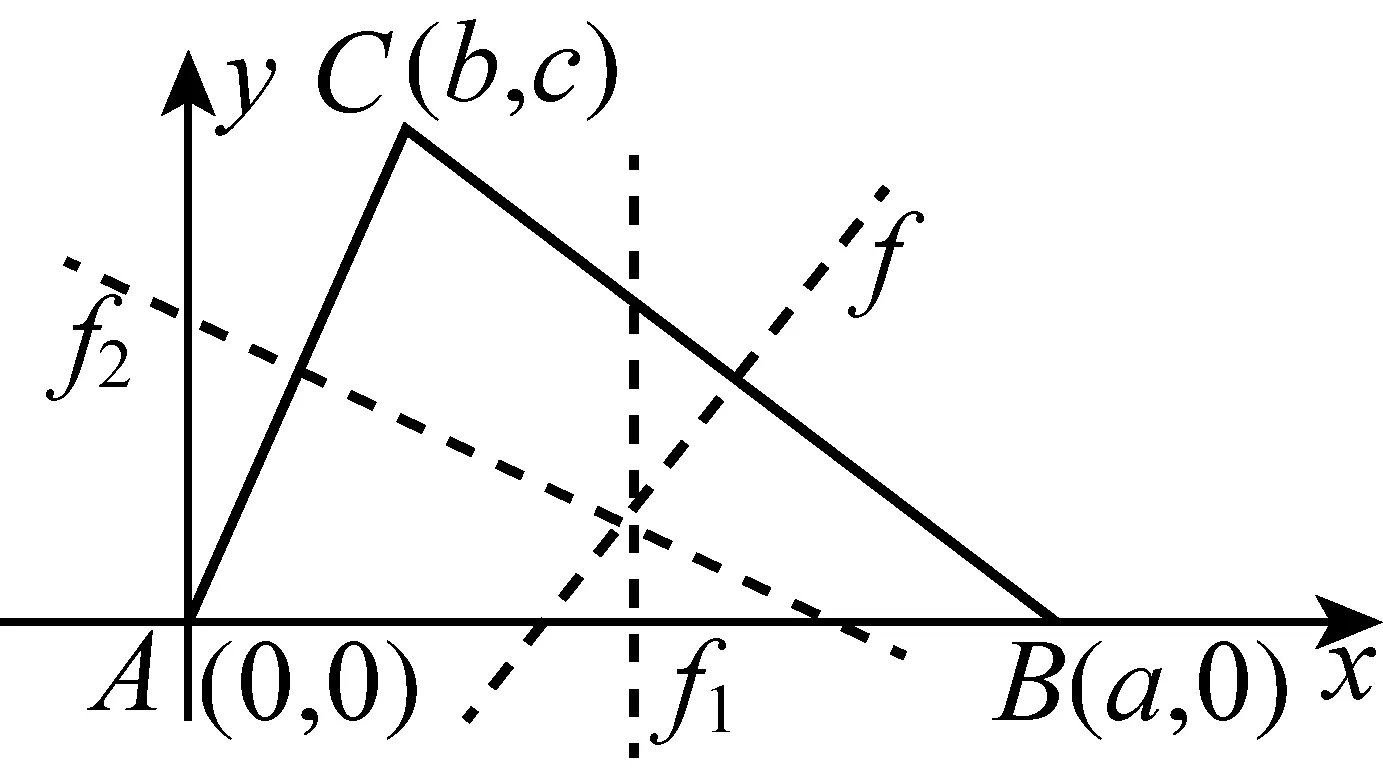
图1

证法1不妨设边AB和AC的中垂线交于点O，则OA=OB，OA=OC，因此OB=OC，O也在边BC的中垂线上.

证法2如图1，设A(0,0)，B(a,0)，C(b,c)，

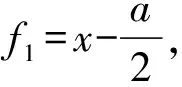
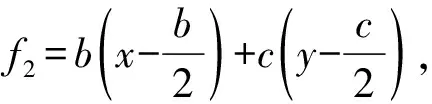
边AC的中垂线方程

因为存在恒等式

因此当点O的坐标满足f1，f2时，也必然满足f.

一般的解析法是从f1，f2中解出公共点O的坐标，然后代入f，判断是否为0.而以吴方法为代表的代数法机械化解几何题，则是研究结论多项式和条件多项式之间的关系，最终希望建立恒等式来证明.因为我们最为关心的是结论是否成立而不是公共点O的坐标.

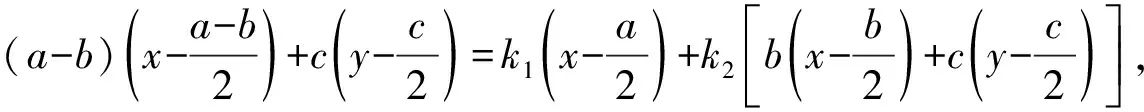
事实上，结合证法1和证法2，可得到证法3.

证法3(OB-OC)+(OC-OA)+(OA-OB)=0.

证法3不是直接去证OB=OC，而是建立一个恒等式.等式右边为0，左边是三项相加，若其中两项为0，那么剩下第三项也必然为0.

我们最近几年的解题实践表明，由于点几何[3-5]表达几何关系比较简洁，若与恒等式思想结合，有很好的效果.具体看实例.

图2

例2如图2，△ABC中，D是BC上的点，若AB⊥AC，AD⊥BC，求证AB2=BC·BD.(直角三角形射影定理)

恒等式：[(A-B)2-(B-C)(B-D)]-(A-B)(A-C)+(B-C)(A-D)=0.

若设A=0，[B2-(B-C)(B-D)]-BC-D(B-C)=0.

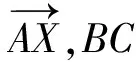
n个多项式相加等于0，其中n-1项都为0，剩余那一项自然为0.这看似平凡的道理，却有妙用.得到恒等式之后，会让我们对几何命题有了更深的认识，譬如此题可推广为：如图2，△ABC中，D是BC上的点，三个条件“AB⊥AC，AD⊥BC，AB2=BC·BD”，任意知道两个，可得第三个.也就是恒等式方法在证明原命题的同时，顺便发现并证明了两个新的命题.而在传统几何中，即便你考虑到研究逆命题，也需要重新加以论证.

下面介绍基于点几何的恒等式如何生成，以及恒等式方法与一般的向量解法如何转化.

先写出条件表达式和结论表达式.AB⊥AC，AD⊥BC，AB2=BC·BD分别写成(A-B)(A-C)=0，(B-C)(A-D)=0，(A-B)2-(B-C)·(B-D)=0.然后设[(A-B)2-(B-C)(B-D)]+k1(A-B)(A-C)+k2(B-C)(A-D)=0，按A、B、C、D展开多项式得A2(1+k1)+BC(1+k1)+BD(1-k2)+CD(-1+k2)+AC(-k1-k2)+AB(-2-k1+k2)=0，解系数方程组1+k1=1+k1=1-k2=-1+k2=-k1-k2=-2-k1+k2=0得k1=-1，k2=1.

如果嫌按部就班操作麻烦，对于项数较少的问题，还可采用观察法.此题不用展开，观察A2的系数，就可得k1=-1，观察CD的系数，就可得k2=1，然后再代入验证整个式子是否为0.

一般的向量法是这样解答：

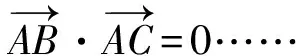
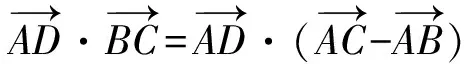
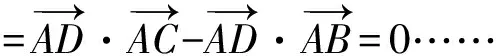
易得①-②-③=0，命题得证.

容易发现，恒等式方法就是一般向量法的综合处理，两者可以相互改写，只是忽视每一项表达式的结果，重点关注结论多项式能否由条件多项式表示.考虑到恒等式方法还未在中学数学领域推广开来，所以建议读者在与人交流，特别是考试答题时要详细说明，或是转化成传统向量解答的形式.

恒等式方法至少有以下优点：

1. 化几何证明为代数计算，操作更简便.在代数恒等式和几何恒等式之间架构了一座桥梁,将几何性质的成立等价于代数式的成立,数形结合更加紧密；

2. 表示简洁,一个等式就完成了证明, 表达甚至比原题更简短，所给出的恒等式证明只需简单计算即可验证,而且几何意义鲜明,读者一看就懂，无需层层递进演绎推理；

3.进行几何充要条件的等价推理,能加深理解条件之间的关系,并产生新的命题,为一题多变研究提供了丰富的素材.

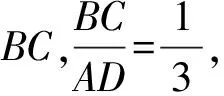
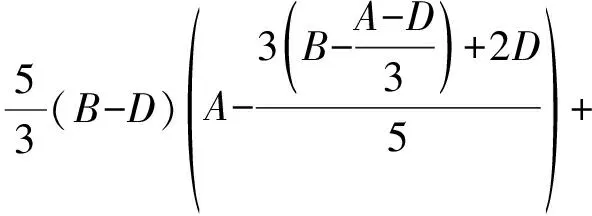
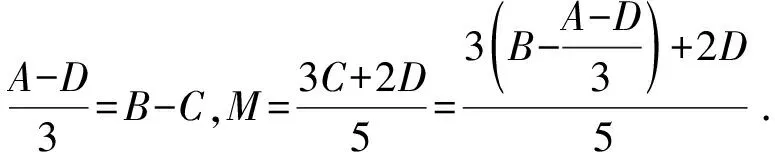
图3

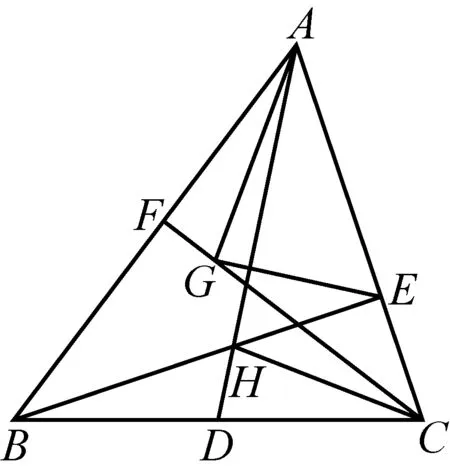
图4

例4如图4，△ABC，D是BC中点，BE、CF是高，G在CF上，AD交BE于H，求证：AD⊥EG⟺AG⊥HC.

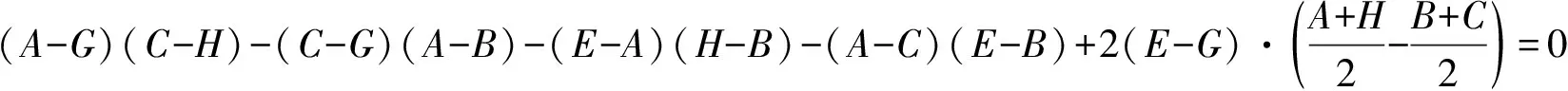
例5如图5，直角梯形ABCD中,AD∥BC,AB⊥BC，E为AB的中点,F为BC的中点,且AD=DC,求证:CE⊥DF.(《数学通报》问题征解1337)

证明

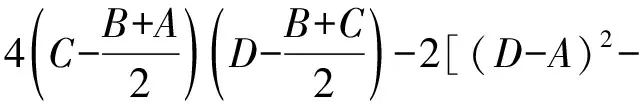
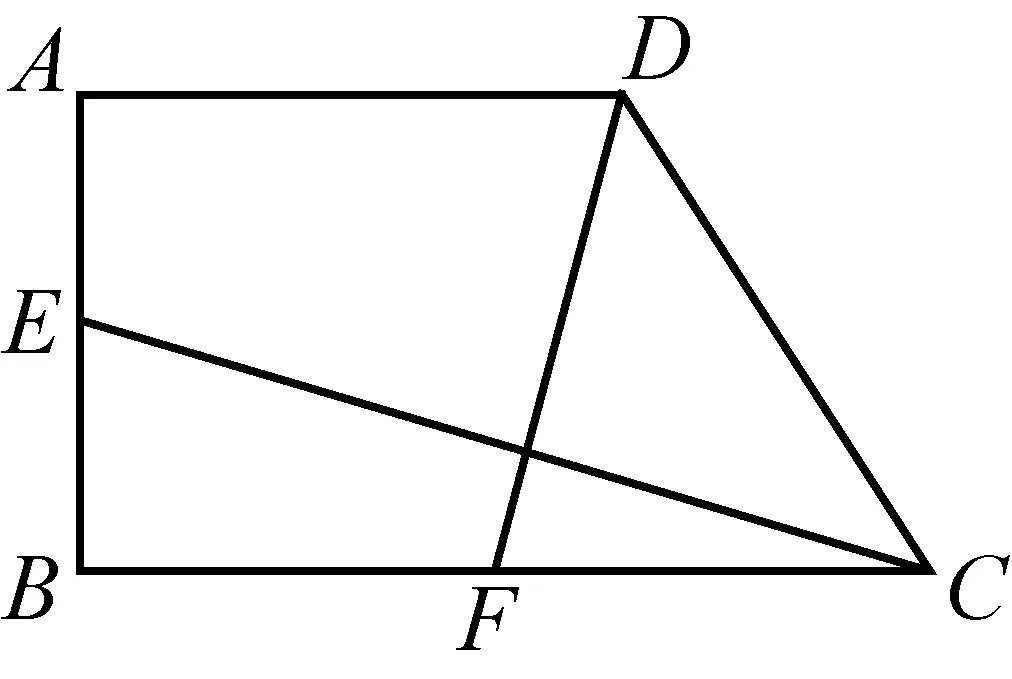
图5

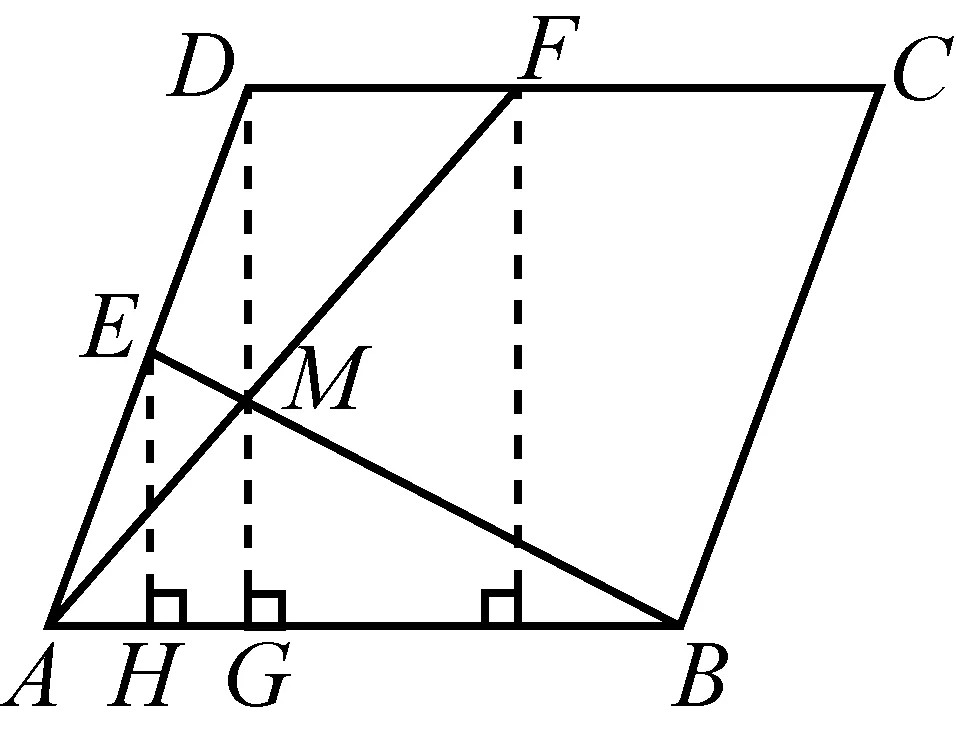
图6

例6如图6，已知E、F分别是菱形ABCD中AD、CD边的中点，BE⊥AF，求证菱形ABCD是正方形.(《数学通报》问题征解1159)

证明

说明：菱形顶点D=A+C-B.

例7如图7，直三棱柱ABC—A1B1C1中,AB1⊥BC1、BC1⊥CA1、CA1⊥AB1 .试证该棱柱是正棱柱.(《数学通报》问题征解1286)

证明B1=A1+B-A，C1=A1+C-A，[(A-B)2-(A-C)2]-(A-A1)(A-B)-(A-A1)(A-C)+(A-B1)(B-C1)-(B-C1)(C-A1)=0.于是(A-B)2=(A-C)2，类似得(A-B)2=(B-C)2.所以该棱柱是正三棱柱.

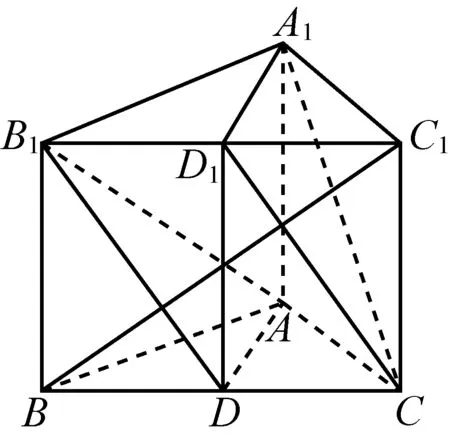
图7

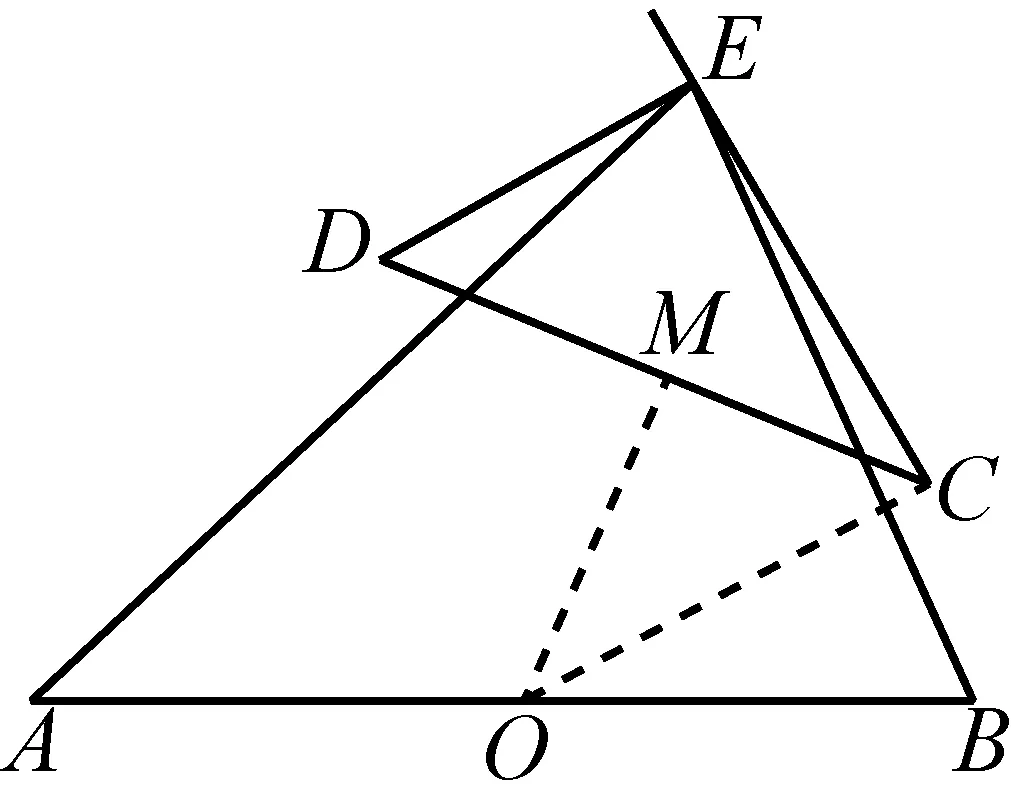
图8

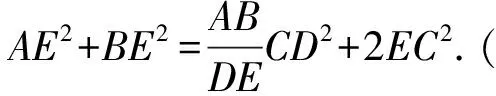
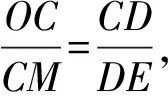
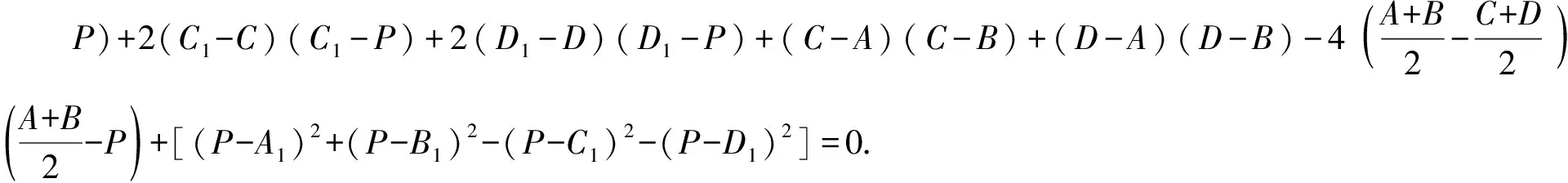
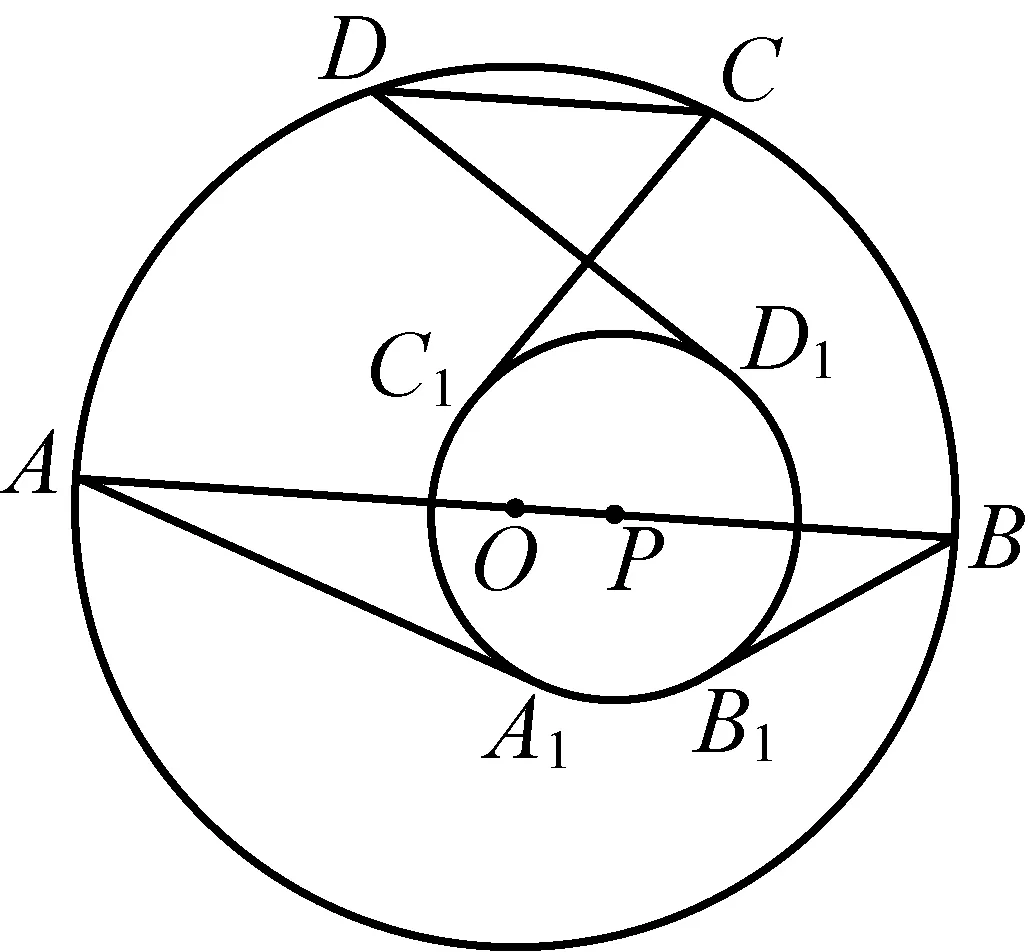
图9

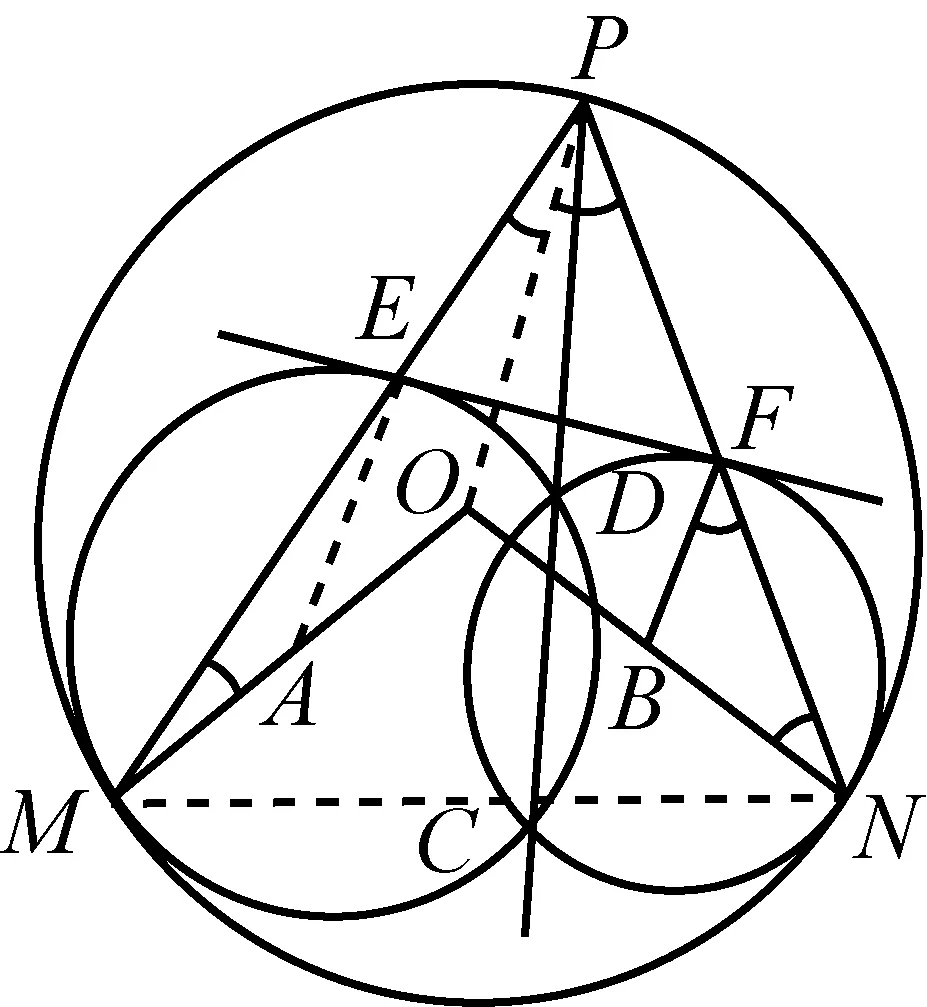
图10

例10如图10，⊙A, ⊙B相交于C、D,且它们都与⊙O内切,切点为M、N,射线CD交⊙O于P，PM交⊙A于E,PN交⊙B于F,证明:EF是⊙A、⊙B的公切线.(《数学通报》问题征解1222)

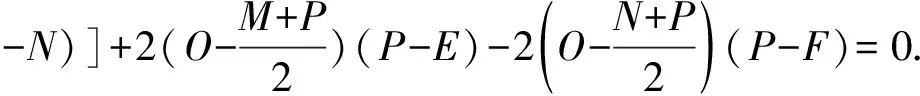
例11如图11，已知凸六边形ABCDEF中,AB=AF,BC=CD，DE=EF.过B作BG⊥AC，过D作DG⊥CE,设BG与DG交点G在△ACE内，求证:FG⊥AE.(《数学通报》问题征解1606)

证明(A-B)2+(C-D)2+(E-F)2-(B-C)2-(D-E)2-(F-A)2+2[(A-C)(B-G)+(C-E)(D-G)+(E-A)(F-G)]=0.

说明：从恒等式可看出，条件“AB=AF,BC=CD，DE=EF”可减弱为

AB2+CD2+EF2=BC2+DE2+FA2.

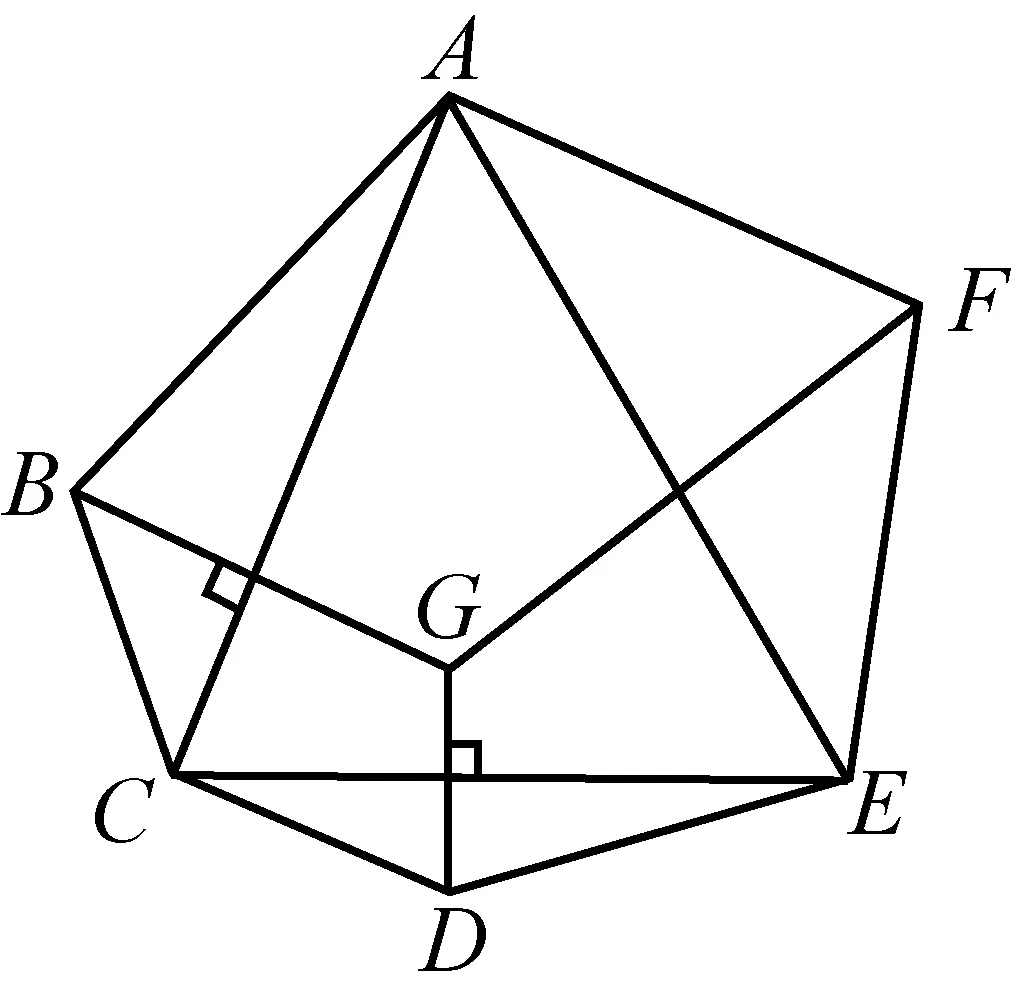
图11

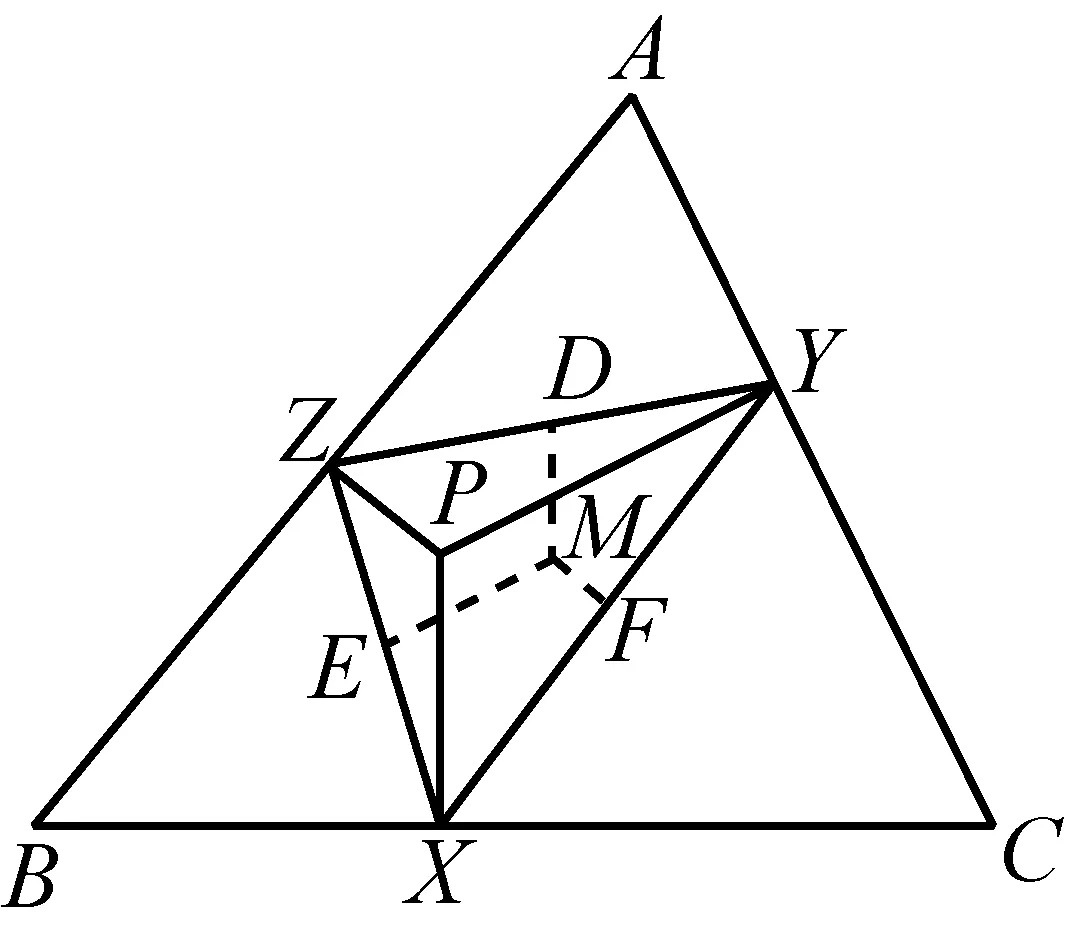
图12

例12如图12，若点P在△ABC三边BC、CA、AB所在直线上的射影分别为X、Y、Z,证明:自YZ、ZX、XY的中点分别向BC、CA、AB所作的垂线共点M.

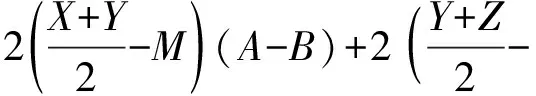
说明1：此题看似复杂，但有着极强的对称性(注意A-B，B-C，C-A这样的式子对称出现)，实际上当写出6个多项式之后，通过观察即可直接写出恒等式.若按部就班解方程组，徒增工作量.

说明2：从恒等式可看出，X未必需要在BC上.其他各点也能进一步放开范围.其余各题也有类似问题，不一一指出.

例13如图13，O、H是△ABC的外心和垂心，O关于BC、CA、AB三边的对称点为X、Y、Z，求证：AX、BY、CZ交于点P，且P是OH的中点.若BC,CA,AB的中点分别为D,E,F,则P为△DEF的外心.(《数学通报》问题征解1130)

证明设O=0，H=A+B+C，X=B+C，Y=A+C，Z=B+A，

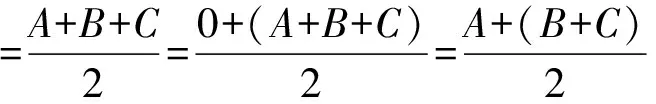
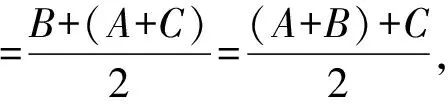
其中R为△ABC外接圆半径.

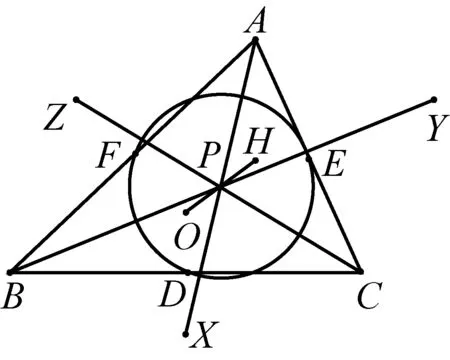
图13

图14

例14如图14，⊙I是△ABC的内切圆.D、E、F是BC、CA、AB上的切点,DD′、EE′、FF都是⊙O的直径;求证:直线AD′、BE′、CF′共点.(《数学通报》问题征解1396)

证明

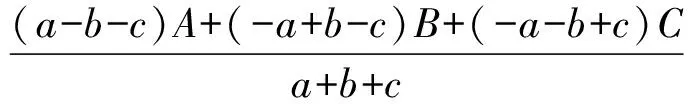
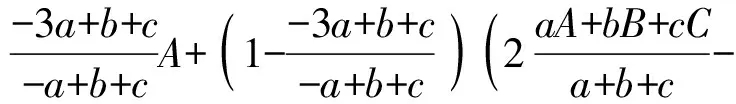
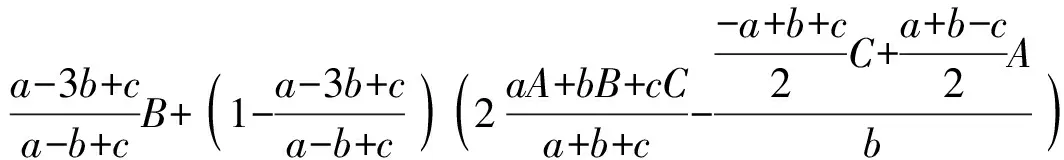
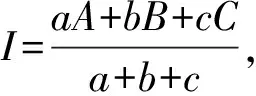
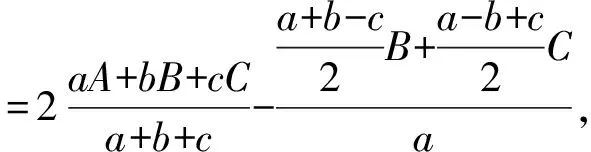
依此类推.

例15如图15，△ABC，内切圆分别与BC、CA交于D、E，在BA延长线上取点F，使得AF=CD，求证：D、E、F三点共线⟺AB⊥AC.

图15

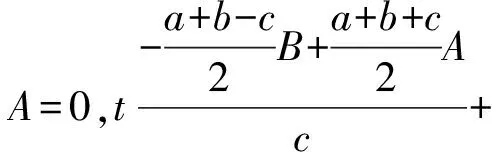
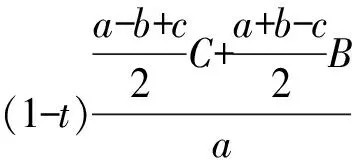
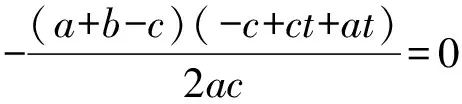
于是得到恒等式

所以D、E、F三点共线⟺AB⊥AC.

恒等式看似短短一行，内涵极其丰富，可以编制新题，但得来却不易.对恒等式解题有兴趣的读者，可以尝试自己动手建立恒等式.如有条件，建议采用计算机.为了更好地与他人交流，恒等式方法与一般向量解法的转换，也需要掌握.