数学问题解答

2019年3月号问题解答

(解答由问题提供人给出)

2471设n是一个大于1的奇数,数a1,a2,…,aφ(n)是1,2,…,n中与n互素的所有正整数.

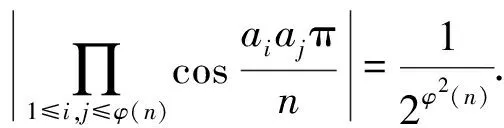
(浙江省富阳二中 许康华 311400)

证明对每一个j∈1，2，…，φ(n),

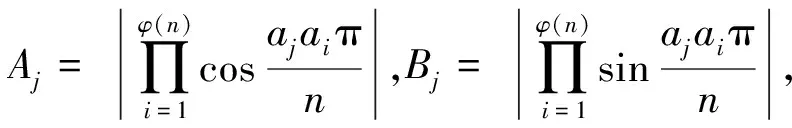
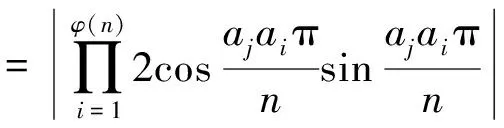
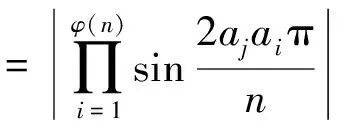
因n是大于1的奇数,而a1,a2,…,aφ(n)是模n的一个缩剩余系,因此对每一个aj而言，aja1,aja2,…,ajaφ(n)以及2aja1,2aja2,…,2ajaφ(n)也都是模n的一个缩剩余系,

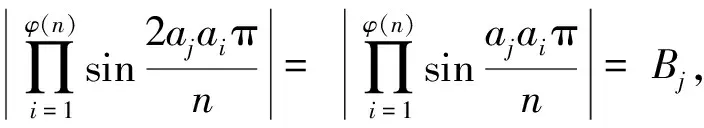
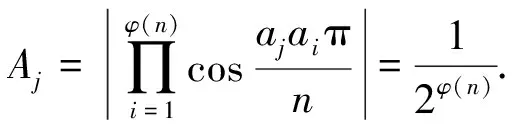
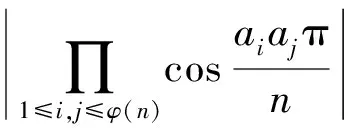
2472设△ABC的三边长、相应的旁切圆半径、外接圆半径、内切圆半径、半周长和面积分别为a、b、c、ra、rb、rc、R、r、p和Δ, 则有

等号当且仅当△ABC为正三角形时成立.

(安徽省太和县第二小学 任迪慧 236630)

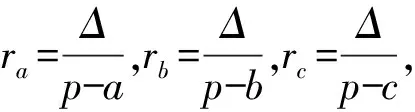
(1)

同理

(2)

(3)

(1)+(2)+(3)整理得

(4)

首先证明左边不等式

△ABC中，有R≥2r,于是可证

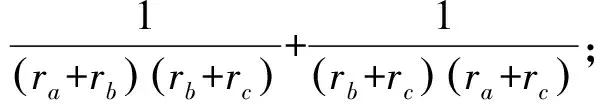
其次证明右边不等式

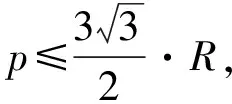
从而可证

从而可证

等号当且仅当△ABC为正三角形时成立.

综上所述，所证不等式成立.

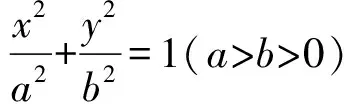
(山东省泰安市宁阳第一中学 刘才华 271400)

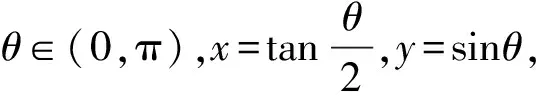
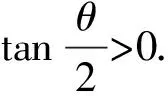
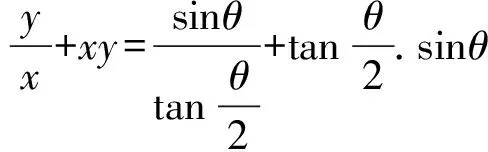
问题的证明：设∠F1PF2=θ，

由椭圆的定义得三角形PF1F2的周长为

PF1+F1F2+PF2=2a+2c，

由熟悉的椭圆焦点三角形面积公式

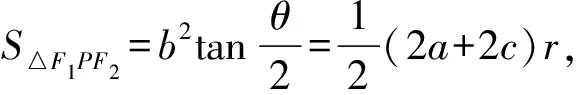
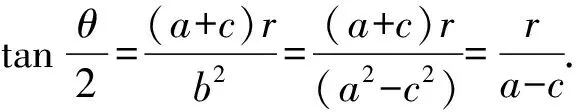
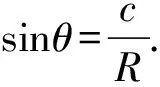
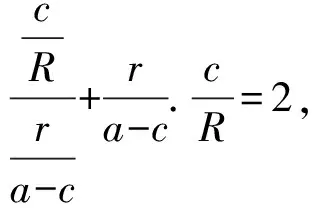
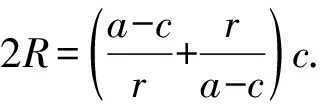
2474已知a,b,c>0，且abc=1，求证：

(广东省广州市广东广雅中学 杨志明 510160)

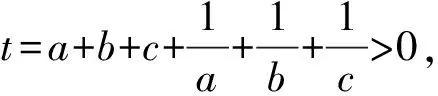
则由均值不等式知，

(1+a)(1+b)(1+c)

=1+a+b+c+ab+bc+ca+abc

故原不等式等价于

⟺(t-2)2≥2(t+2)

⟺t2-6t≥0⟺t(t-6)≥0．

显然成立，证毕．

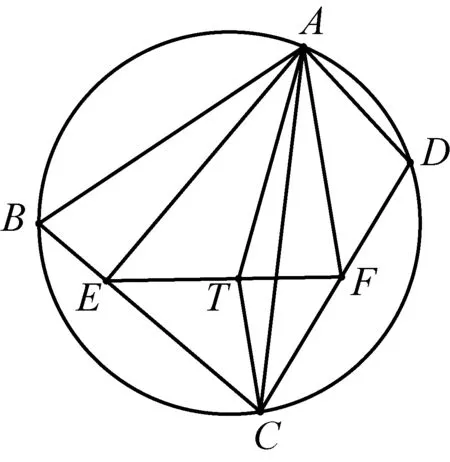
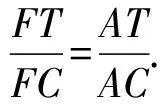
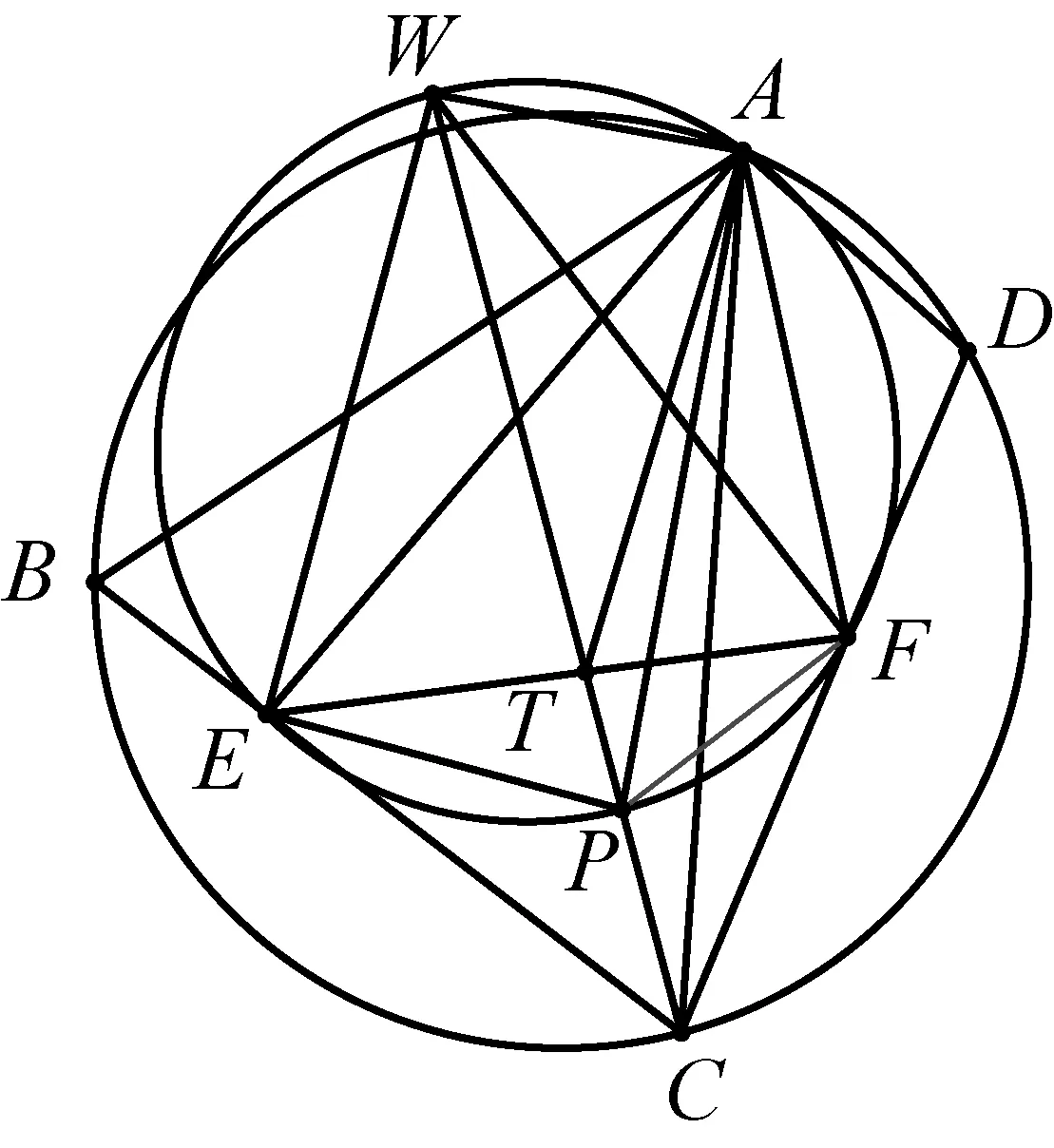
(江西师范高等专科学校 王建荣 335000)

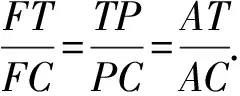
2019年4月号问题
(来稿请注明出处——编者)

2476已知a,b,c≥0,a+b+c=3,求证: 4≤a2+b2+c2+abc≤9.

( 陕西省咸阳师范学院基础教育课程研究中心 安振平 712000 )

2477求证：在a+bn(n∈N*)的展开式中有2sn个系数为奇数．其中sn是n在二进制表示中的数字和．

(湖北省谷城县第三中学 贺斌 龚为民 441700)

2478已知如图，五边形ABCDE内接于⊙O，且BC=DE，∠EAB=120°.求证：AC·AD≤(AB+AE)2.

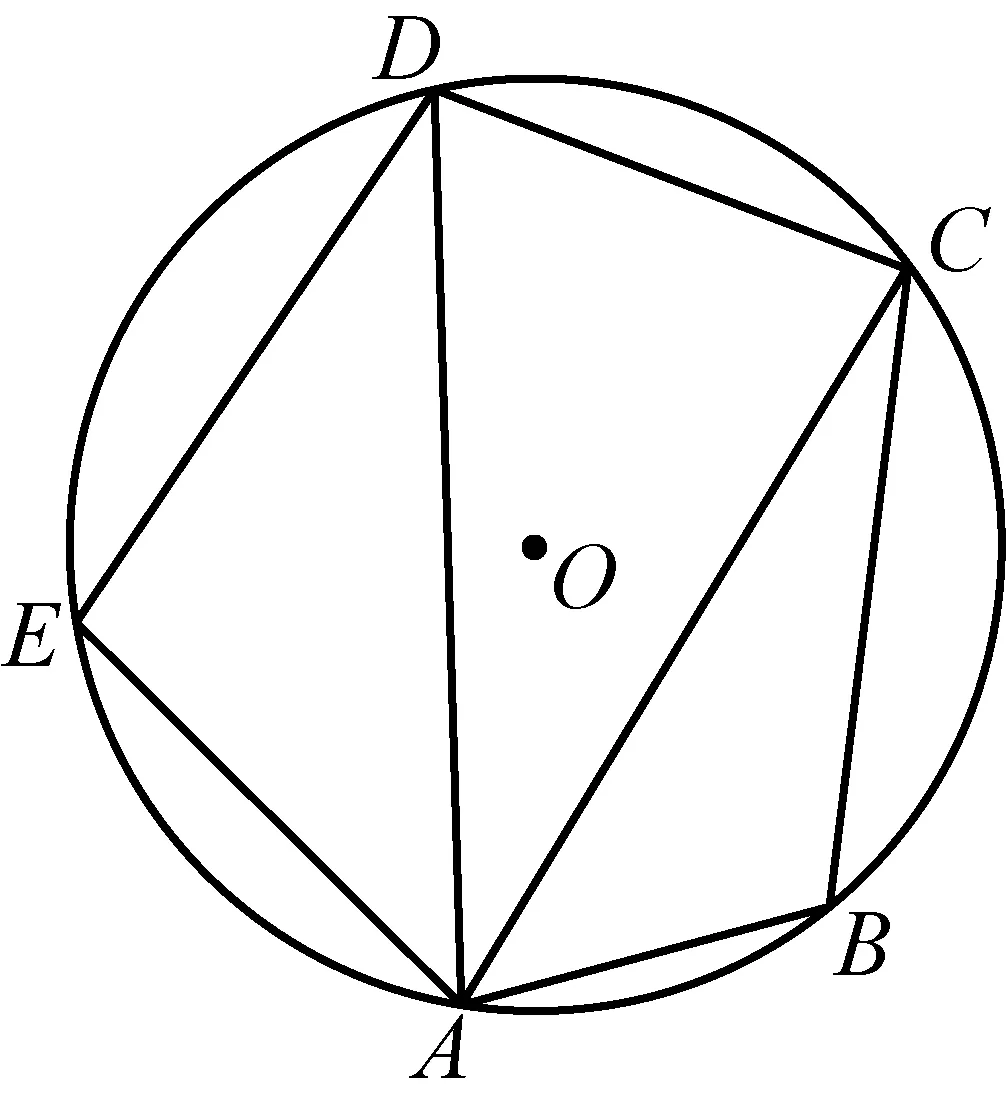
(北京市芳草地国际学校富力分校 郭文征 郭璋 100121)

2479已知a1,a2,…,an(n≥2)为实数，求证：

(浙江省海盐县元济高级中学 张艳宗31430；北京航空航天大学图书馆 宋庆 100191 )

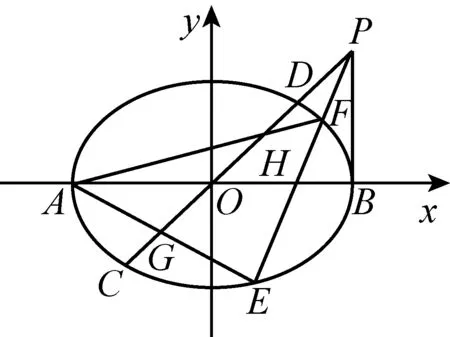
(浙江省慈溪市慈溪实验中学 华漫天 315300)