相对失控翻滚目标悬停的自适应模糊滑模控制
刘将辉,李海阳,张政,李晓超
国防科技大学 空天科学学院,长沙 410073
在轨航天器价值大、造价高,当其在空间中发生失效时,如果能对其进行在轨修复、部件更换和燃料加注,则可以大幅降低任务成本,因此受到了研究人员的极大关注[1-7]。相对悬停,通常表示一个航天器在另一个航天器的体坐标系中具有不变的位置和不变的姿态。实现相对悬停,可以对目标航天器实施空间监视或检查[8]。
历史上,相关研究主要集中在相对小行星的悬停。1999年,Scheeres首次提出了航天器相对小行星悬停轨道的概念[9]。一般而言,围绕小行星悬停的方式主要有惯性悬停和目标体坐标系悬停[8,10]。Broschart和Scheeres对小引力作用下的小行星的悬停控制问题进行了数值模拟,确定了惯性悬停的稳定区域[8]。在相对小行星的悬停控制中,为了维持所期望的位置,航天器需要连续使用控制推力以抵消重力和旋转加速度[10-11]。由于航天器的标称加速度很小,这种方法在小行星上是可行的[8-9,12]。Zeng等提出了利用太阳帆航天器对小行星进行悬停,由于没有燃料消耗,大幅度延长了悬停时间和扩大了悬停位置范围[13]。应该指出的是,前期航天器相对小行星悬停的研究主要集中在航天器与小行星的相对位置控制,而无考虑相对姿态的控制[8-10,12,14-16]。Lee等在几何力学的框架中提出了相对小行星悬停的相对位置和相对姿态的无源跟踪控制[17]。针对低速旋转小行星悬停的轨道和姿态控制问题,Lee等设计了一个连续的有限时间收敛的控制方案[18-19]。
严格来说,航天器相对小行星的悬停问题不同于相对目标航天器的悬停问题。这是因为前者需要同时考虑小行星和太阳的引力影响,而后者只需考虑地球引力的影响,因此这两种情况下的动力学控制方程也各不相同。
在本文中,主要研究一个航天器相对另一个航天器的悬停控制问题。最近,一些研究人员在两航天器间的悬停控制方面也发表了许多研究成果。谭天乐对两航天器在近圆、椭圆轨道上的相对运动分别进行了解析求解,采用矩阵广义逆变换的方法设计控制器,通过模型预测的方法获得制导偏差[20-21]。薛白等建立了两航天器间悬停的混杂系统模型[22]。程博等基于航天器间的状态转移矩阵描述,采用多脉冲控制方法研究相对悬停运动[23]。徐帷针对超近距离的两航天器间的悬停问题,在相对轨道控制的基础上,提出了视线指向跟踪的控制方法,实现了相对轨道、姿态的联合控制[24]。宋旭民等基于Hill方程研究了悬停闭环控制方法[25]。Dang等建立了两航天器间悬停的精确解析解模型,推导了轨道周期内的最小推力和最小燃料位置[26]。Sun和Huo研究了航天器间姿轨耦合和考虑模型不确定的位姿控制[27]。
然而,前面有关悬停控制的研究主要关注两航天器间相对位置的控制,相对姿态控制方面的研究不多,悬停控制方式也以开环的形式居多。即使有考虑相对姿态控制问题,也只是考虑目标姿态稳定或姿态变化缓慢的情况。考虑到前面研究的局限性,有必要进一步对两航天器间悬停控制问题进行研究,本文针对追踪器相对空间中姿态变化较快的目标器的悬停控制问题进行了研究。在追踪器本体坐标系中建立了非线性的六自由度耦合的一体化动力学模型,基于模糊逼近原理设计了一种自适应的模糊滑模控制器,该控制器能够有效地克服系统不确定性和外部干扰的影响,并能消除传统的抖振问题。最后,通过数值仿真检验了自适应模糊滑模控制器的有效性。
1 动力学模型

(1)
满足:ζTS(ζ)=0,对于任意向量ξ=[ξ1,ξ2,ξ3]T有,ξTS(ζ)ξ=0。
(2)
1.1 位置和姿态动力学模型

追踪器相对于惯性系FE的位置和姿态动力学模型为[27]
(3)
式中:υc和ωc分别为追踪器体坐标系FC描述的追踪器的速度矢量和角速度矢量;σc为用修正的罗德里格斯参数(Modified Rodrigues Parameters,MRP)描述的追踪器体坐标系FC相对于惯性系FE的姿态;mc为追踪器的质量;Jc为追踪器的转动惯量矩阵;Fc和τc分别为追踪器的控

图1 相对位姿运动坐标系统Fig.1 Relative position and attitude motion coordinate system
制力和控制力矩;Fcd和τcd分别为追踪器所受的未知有界干扰力和未知有界干扰力矩;δ为作用在追踪器的推力到追踪器质心的偏心矢量。
类似地,失控翻滚目标器相对于惯性系FE的位置和姿态动力学模型为[27]
(4)
式中:υt和ωt分别为目标器体坐标系FT描述的目标器的速度矢量和角速度矢量;σt为目标器体坐标系FT相对于惯性系FE的姿态;Jt为目标器的转动惯量矩阵;Ftd和τtd分别为目标器所受的未知有界干扰力和未知有界干扰力矩。
1.2 相对运动动力学模型
通过MRP描述的追踪器体坐标系FC相对于目标器体坐标系FT的姿态为[28]
(5)
对应的姿态转移矩阵为
(6)
由图1可知,悬停点H相对于FE的位置矢量和速度矢量在目标器体坐标系FT中的描述分别为
rd=rt+hf
(7)
υd=υt+S(ωt)hf
(8)
在追踪器体坐标系FC中描述的两航天器相对角速度矢量、相对位置矢量和相对速度矢量分别为
ωe=ωc-Meωt
(9)
re=rc-Merd
(10)
υe=υc-Meυd
(11)
(12)
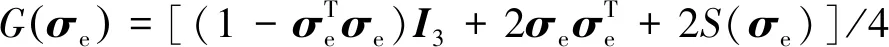
-S(Meωt)[Meυd-MeS(ωt)hf]+
[υc-υe-S(ωc-ωe)Mehf]+
(13)
(ωc-ωe)-τtd}
(14)
因此,式(12)可以改写为
(15)
式中:
1.3 一体化动力学模型
(16)
(17)
式中:
注1模型(16)中的A1和模型(17)中的B1和B2都反映出了两航天器间的相对姿态运动影响相对位置运动,这说明两航天器间的相对姿态和相对位置运动存在强烈的耦合效应。
本文对模型(16)和(17)给出如下假设条件:
1) 整个悬停过程中,由于燃料消耗较少,mc和Jc保持不变,δ为未知常向量。
2) 追踪器可以通过自身的测量装置获取自身的运动信息{rc,υc,σc,ωc}和相对运动信息{re,υe,σe,ωe}。

2 控制器设计与稳定性分析
2.1 滑模函数
考虑系统的模型不确定性,式(17)进一步转化为
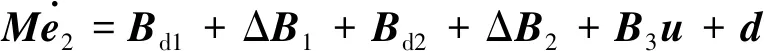
(18)
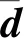
(19)
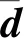
(20)

(21)
式中:M-1为M的广义逆矩阵;f(X)为未知函数。跟踪误差矢量e及de分别定义为
e=X1
(22)
de=X2
(23)
滑模函数设计为
s=de+ce
(24)
式中:c为滑模函数系数,c=diag(c1,c2,…,c6),ci>0,i=1,2,…,6。则
(25)
由式(24)可知,如果s→0,则e→0且de→0。
2.2 模糊逼近原理
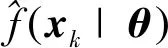
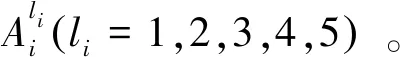
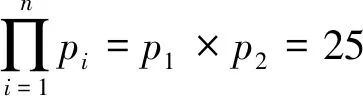
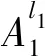
j=1,2,…,25
(26)
式中:则第1条和第25条模糊规则表示为
(27)
模糊推理过程采用如下4个步骤[29]:

4) 采用平均解模糊器,得到模糊系统的输出为
(28)
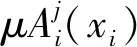

(29)

(30)
2.3 控制器设计与稳定性分析

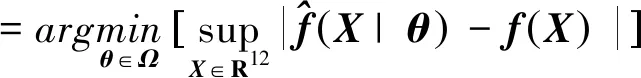
(31)

(32)
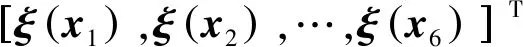

(33)
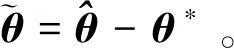
定义Lyapunov函数为
(34)
式中:γ>0。对V求导可得
(35)
将式(25)代入式(35)可得
(36)
设计控制律为
(37)
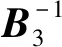
(38)

自适应律为
(39)



3 仿真分析
在本节中,以追踪器对失控翻滚目标的近距离悬停为例,通过仿真来验证所设计控制器的有效性。为了便于对比分析,本文仿真参数采用文献[27]的数据。hf=[0, 5, 0]Tm,σe0=[0, 0, 0]T,δ=[0.02, 0.03, 0.02]Tm。追踪器的初始位置为rc(t0),初始速度为υc(t0),初始姿态为σc(t0),初始角速度为ωc(t0);目标器的初始姿态为σt(t0),初始角速度为ωt(t0);初始相对位置为re(t0),初始相对速度为υe(t0),初始相对姿态为σe(t0),初始相对角速度为ωe(t0)。以上各参数数值详见表1。

表1 仿真参数Table 1 Simulation parameters
追踪器的质量为mc=58.2 kg,
干扰力矩τcd、τtd和干扰力Fcd、Ftd分别为

取以下5种隶属度函数对模糊系统输入xk=[x1,x2],k=1,2,…,6,进行模糊化
(40)
根据式(40)可以得到xi的隶属函数如图2所示。

图3为目标器的姿态和角速度变化曲线,从图中可以得出,目标航天器在空间中做自由翻滚运动,其姿态σt和角速度ωt按照一定的规律进行变化,变化情况由其转动惯量分布和初始角速度共同决定。
图4为追踪器和目标器的相对姿态和相对角速度变化曲线。经过58 s,相对姿态从[0.5, -0.6, 0.7]T降到03×1,相对角速度从[0.02,

图2 xi的隶属函数Fig.2 Membership function degree of xi

图3 目标器的姿态和角速度变化Fig.3 Attitude and angular velocity of target
-0.02, 0.02]Trad/s开始迅速增大,到了峰值后又逐渐降到03×1rad/s。说明追踪器对失控翻滚目标完成了姿态捕获并在之后与目标器保持姿态同步。文献[27]完成相应的姿态同步需要80 s,本文比文献[27]少22 s。
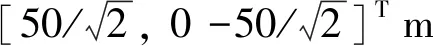
图6为追踪器的控制力矩和控制力随时间变化曲线。在初始时刻,为了捕获目标器的姿态,追踪器需要输出较大的控制力矩,为[-16.03, 15.58, -9.73]TN·m,经过52 s,追踪器所需的控制力矩极小,各方向最大的控制力矩不超过0.15 N·m,初始时刻,追踪器需要较大的控制力,为[18.79, -15.20, -28.95]TN,经过76 s,追踪器所需的控制力极小,各方向的最大的控制力不超过0.5 N。整个过程追踪器的控制力矩和控制力曲线光滑平缓,无抖振现象发生。文献[27]中各方向所需的最大控制力矩幅值为60 N·m,最大控制力幅值为40 N,本文方法所需各方向的控制力矩幅值和控制力幅值与文献[27]相比均较小,更具有实际操作性。
为了验证所提的自适应模糊滑模控制器的有效性,有必要与传统滑模控制器进行对照。在没有模糊自适应条件下,式(37)在传统的滑模控制结构中可以表示为

(41)
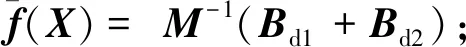

图4 相对姿态和相对角速度Fig.4 Relative attitude and angular velocity

图5 相对位置和相对速度Fig.5 Relative position and velocity

图6 追踪器的控制力矩和控制力Fig.6 Control torque and control force of the chaser
其他各仿真参数均与自适应模糊滑模控制器相同,仿真结果如图7~图9所示。通过将图7~图9 与图4~图6对比可以得出,传统滑模控制器作用下,追踪器与目标器完成姿态同步和位置同步分别需要64 s和67 s,比自适应模糊滑模控制器长6 s和8 s。传统滑模控制器输出的控制力矩和控制力均出现了抖振现象。滑模控制器的MPE2=1.809 9。很显然,自适应模糊滑模控制器有效的改善了闭环系统动态响应性能。
为了研究自适应模糊滑模控制器的鲁棒性,将外部有界摄动力Fd和外部有界摄动力矩τd分
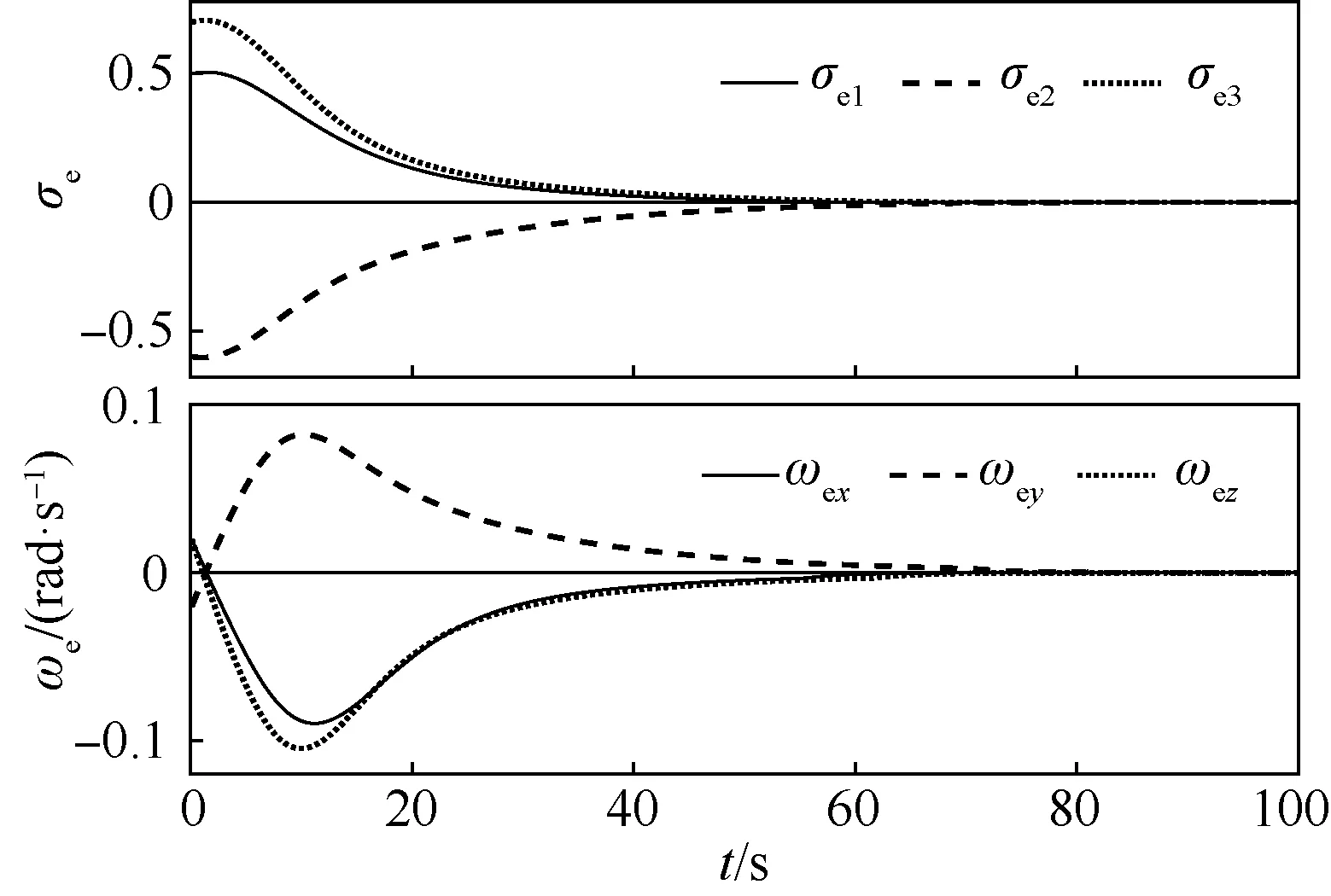
图7 滑模控制下的相对姿态和相对角速度Fig.7 Relative attitude and angular velocity under sliding mode control

图8 滑模控制下的相对位置和相对速度Fig.8 Relative position and velocity under sliding mode control

图9 滑模控制下追踪器的控制力矩和控制力Fig.9 Control torque and control force of chaser under sliding mode control
别扩大到100Fd和100τd,其他仿真参数均不变,仿真结果如图10~图12所示。通过将图10~图12与图4~图6相对比,可以发现,在经过58 s追踪器完成了对逼近点的位置同步。经过59 s追踪完成了对目标器的姿态同步。控制力矩和控制力曲线均光滑平缓,无抖振现象,平均性能误差指数MPE3=1.567 9。与小干扰情况下的控制性能一样,说明所设计的自适应模糊滑模控制器具有较强的鲁棒性。
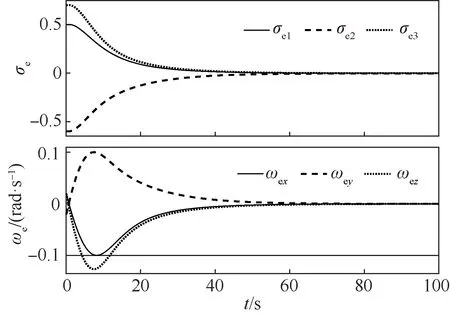
图10 大扰动下的相对姿态和相对角速度Fig.10 Relative attitude and angular velocity under large disturbance
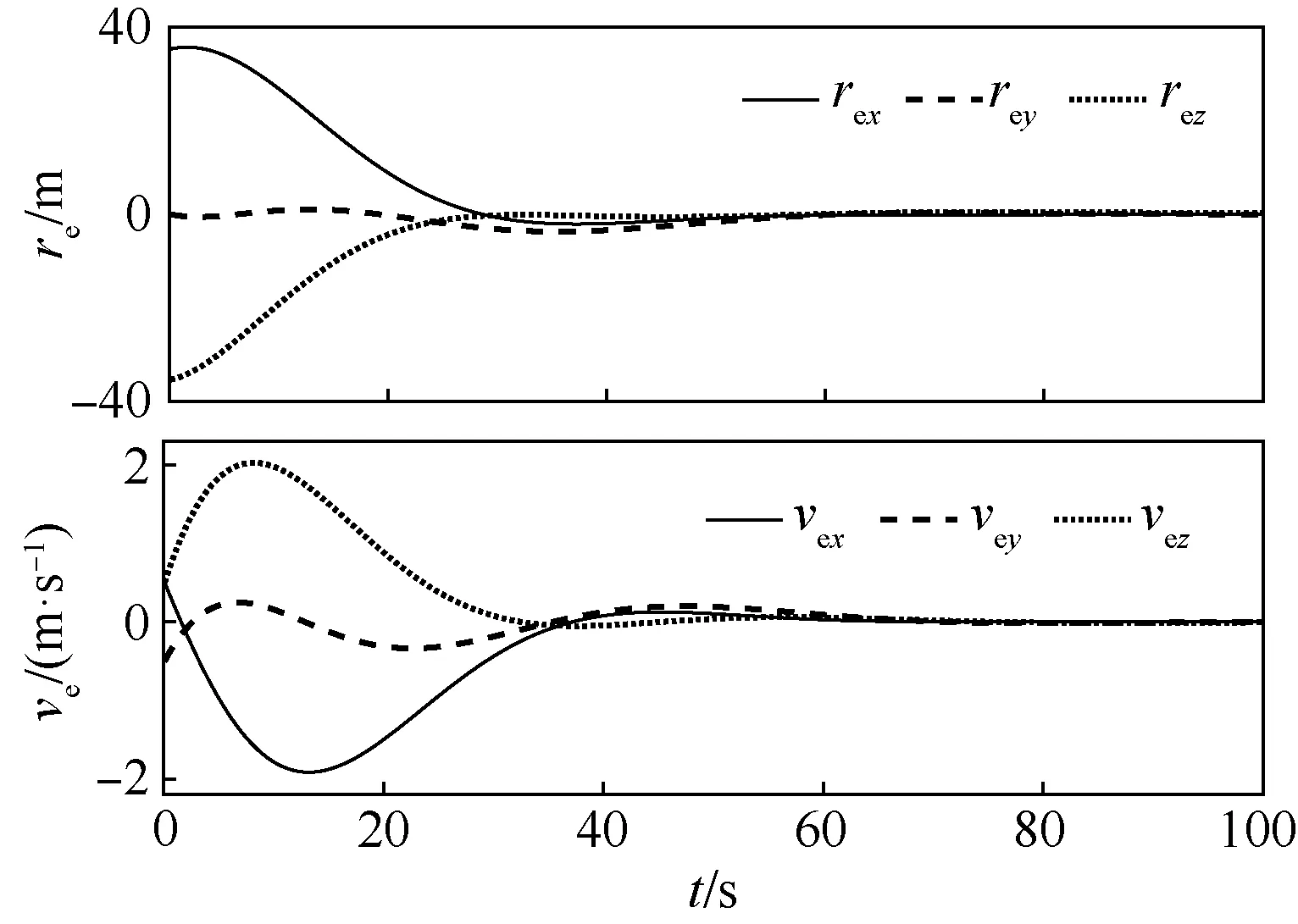
图11 大扰动下的相对位置和相对速度Fig.11 Relative position and velocity under large disturbance

图12 大扰动下追踪器的控制力矩和控制力Fig.12 Control torque and control force of chaser under large disturbance
4 结 论
1) 本文利用追踪器相对失控翻滚目标悬停时的可测信息设计了自适应模糊滑模控制器,实现了六自由度耦合的相对位置与相对姿态控制。
2) 基于模糊系统的万能逼近原理设计的模糊滑模控制器能有效地实现对系统未知部分的自适应逼近。该控制器能够有效克服系统的模型不确定性和外部干扰因素的影响。
3) 追踪器快速到达了翻滚目标器的悬停位置,悬停位置误差和悬停速度误差均收敛到较小的范围内。所需的控制力矩和控制力极小、连续平滑,无抖振现象发生。

