跨声速风洞斜孔壁非线性流动试验

刘光远，张林，陈德华，林学东，贾智亮

1.中国空气动力研究与发展中心 空气动力学国家重点试验室，绵阳 621000 2. 中国空气动力研究与发展中心 高速空气动力研究所，绵阳 621000

跨声速风洞孔壁在降低堵塞干扰和波反射干扰的同时，也在近壁区域诱导出沿壁板法向的穿孔流动，该流动不仅影响设备的调试和运行，而且关系到洞壁干扰特性以及数据的评估和修正，是跨声速风洞试验领域的主要难题之一。

孔壁流动特性研究起始于20世纪60年代，前期研究主要集中于简化建模[1]，认为壁板压差与气流偏角之间存在线性关系，目前国内外生产型风洞应用的工程洞壁干扰评估/修正体系[2-5]均建立在该线性模型的基础上。而实际上，穿孔流动特性不仅受孔壁几何参数和边界层特性的影响，还与试验模型状态和马赫数密切相关，边界条件并非完全线性。

国外研究者采用试验和计算方法对孔壁流动非线性问题开展了广泛的研究[6-8]，提出对孔壁流动特性影响最大的两个因素为边界层位移效应，模型扰流导致的流线弯曲和穿孔流动之间的耦合干扰。边界层影响方面，Chan分析了穿孔流动方向对边界层的影响，发现孔壁流动特征曲线的斜率在出流区域比入流区域高1倍以上[9]；Doerffer和Neyland等分别利用吹吸气[10]和翼型升力[11]改变边界层状态，发现随着孔壁边界层厚度的增大，流动特征曲线的斜率降低，孔壁特性趋于开口边界；Ivanov对直孔流动进行了深入分析，认为边界层位移厚度与孔直径的比值大于1时，孔壁流动特性将出现明显的非线性特征[12]。模型扰流影响方面，Goffert等在空风洞和有翼型条件下研究了孔壁近壁区域流场[13-14]，发现模型在壁面诱导出沿流向变化的穿孔流动；Semenov和Semenova在孔壁出/入流区域分别给定不同的特性参数，得到的壁面压力分布与试验结果的吻合程度远高于线性模型计算结果[15]；Glazkov等认为模型升力对孔壁边界层的诱导作用将导致孔壁不同区域流动特性出现差异，使用同一参数进行修正是不准确的[16-17]。

除孔壁非线性流动的机理研究外，国外研究者还开展了初步的非线性建模工作。美国阿诺德工程发展中心(Arnold Engineering Development Center，AEDC)Crites等测试了多副直孔试验件流动特性，提出了包括边界层厚度的非线性模型[18-19]，但忽略了马赫数和开孔角度的影响；Harloff和Smith基于喷管流动方程提出了著名的Harloff模型[20]，Akatsuka等对该模型进行了试验验证[21]，表明其过高地估计了入流区域的流量，Harloff模型仅在大压差状态有效，并不适用于亚、跨声速的小压差状态；Nambu等对单孔流场进行数值模拟，并针对JTWT洞体条件建立了孔壁流动非线性数学模型[22]，成功应用于二元翼型[23]和ONERA-M5模型[24-25]的洞壁干扰修正中，取得了较好的效果。以上试验测试和建模研究对于深入分析孔壁流动机理、发展非线性数学模型具有重要的意义，但它们的对象仅限于直孔壁，目前尚未开展过斜孔壁流动特性的研究工作；此外，所获得的定量结果和数学模型中的系数随风洞运行条件和模型状态参数变化，通用性较差。

国内方面，周长海在20世纪90年代开展了孔壁局部区域流动特性的数值模拟工作[26-27]，得到了法向扰动速度与当地流动参数的依赖关系；曹世坤采用与Nambu类似的方法，对简化的单孔流动进行数值模拟[28]，加深了对孔壁流动特性的理解。但以上数值模拟工作均未进行试验验证，国内风洞设备目前多采用基于线性边界条件的壁压信息法，或结合壁压分布的CFD非线性方法[4,29]进行孔壁干扰修正工作。近年来，中国空气动力研究与发展中心(CARDC)进行了孔壁开闭比、开孔分布等对核心流均匀性的影响研究[30]；刘琴等利用孔壁和型面喷管获得了马赫数Ma=1.40的均匀流场，拓宽了孔壁的适用范围[31]；丛成华等利用多孔介质模型计算了开闭比对低超声速流场的影响[32]。但以上研究的重点是合理开孔分布的选择，对近壁区域流动特性的关注较少，与国外相比，研究深度和广泛性均存在较大差距。

深入理解孔壁流动机理是孔壁设计以及干扰修正的基础，发展孔壁流动特性研究手段对开展设备设计、调试及数据相关性研究具有重要的指导意义。本工作利用七孔探针试验测量了斜孔壁流动特性，以气流偏角和压力分布为指标，分析了马赫数、模型升力对孔壁流动的影响，并提出了计算斜孔壁特性参数Q的微分法，以期为将来开展跨声速风洞孔壁流动非线性建模和干扰修正工作提供借鉴。

1 孔壁特性参数Q

孔壁流动特性多采用孔壁诱导的法向、流向扰动速度之间的关系来描述，将扰动速度写为气流偏角θ和压力系数Cp的形式，得到的θ-Cp关系称为孔壁流动特征曲线。简化的线性模型认为该曲线是直线，θ、Cp之间满足Darcy定律[1]：

θ=0.5RCp

(1)

式中：R为Darcy系数，量值为特征曲线斜率的2倍。孔壁特性参数Q定义为R的归一化函数：

(2)

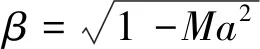
Q值是孔壁干扰评估和修正的关键，堵塞干扰因子、升力干扰因子等均为Q值的函数。目前工程中多采用Neiland经验公式[33]或参考无干扰数据的比较测量法获得Q值。Neiland公式为

(3)

式中：τ为孔壁的开闭比。得到R值后，代入式(2) 计算Q值。线性理论认为，对于指定的孔壁，系数R为定值，Q随Ma增大而略增大。

2 流动特性测量试验

2.1 试验设备

斜孔壁流动特性测量试验在CARCD 0.6 m跨超声速风洞中开展，试验段尺寸为0.6 m×0.6 m，左右为实壁，上下为60°斜孔壁，开闭比为5.7%，孔径和壁厚均为12 mm。

试验扰动模型采用GBM-04A标模，该标模具有截尖三角形机翼和后掠平尾常规布局，全长640 mm，展长311 mm。试验中采用尾支撑，0°迎角时在风洞中的堵塞度为1.04%。

2.2 试验方法与仪器

试验分为空风洞和有模型两部分内容，利用安装于试验段上壁板的探针测量斜孔壁近壁区域流动的气流偏角和压力，并评估马赫数和模型升力对孔壁流动的影响。

采用的探针为AeroProbe公司生产的PS5型七孔探针，该探针头部为60°圆锥，全长152.0 mm，头部直径为3.18 mm。安装位置距离孔壁表面48 mm，即4倍孔径位置处，以避开斜孔导致的局部波动。探针沿气流方向(简称“流向”)分别测量了加速区、模型区和支架区的流动特性，距试验段入口距离分别为0.12、0.45和0.65倍试验段长度。为便于对比，定义驻室向试验段方向的入流为气流偏角的正方向，图1给出了试验照片。

图1 0.6 m风洞试验照片Fig.1 Picture of 0.6 m wind tunnel test

2.3 数据处理方法

基于Grubbs准则剔除结果中的坏点。以气流偏角θ为例，首先按照最小二乘法进行多项式拟合：

θfit(T)=A0+A1T+A2T2+A3T3

(4)

式中：T为拟合变量，可以选取为马赫数Ma或模型升力系数CL；A0～A3为拟合系数。

然后计算各测点值与拟合值之间的残差：

(5)

式中：N为总的测点数;i为测点序号。

(6)

最后对剔除坏点后的数据再次进行Grubbs分析，直至所有点均在置信区间以内。

2.4 探针测量精度

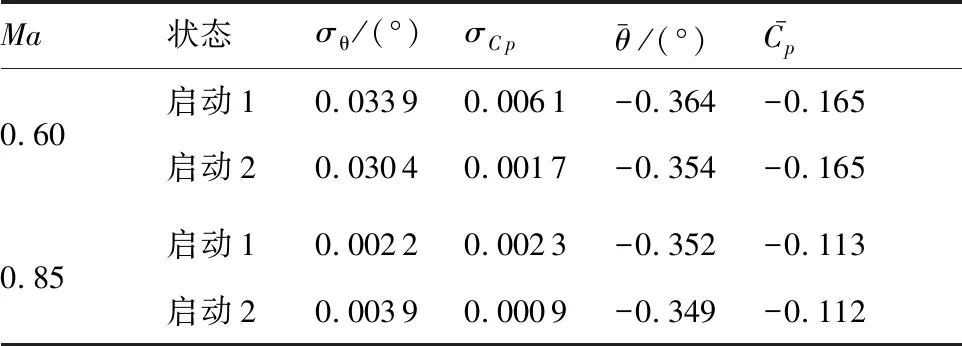
表1 七孔探针测量稳定性和重复性Table 1 Stability and repeatability of seven-hole probe measurement

从表1可以看出，风洞同一启动内测值稳定，波动量随Ma增大而减小，气流偏角和压力系数的均方根偏差分别小于0.035°和0.007；两次启动间气流偏角和压力系数测值差异分别小于0.01° 和0.001。说明七孔探针可较准确地测量孔壁区域的流动特性。

2.5 计算系数Q的微分法

由Q系数的定义(式(2))可知，测得孔壁压力系数和气流偏角后，可以直接计算系数值，但计算结果中包含了探针的零飘、安装等系统误差，而且无法评估Ma和模型升力的影响。因此，本项目发展了一种求解R、Q的微分法，比较不同Ma或模型升力时的差量，可以消除探针的系统误差。

首先对气流偏角和压力系数进行多项式拟合：

θ=A0+A1T+A2T2

(7)

Cp=B0+B1T+B2T2

(8)

式中：A0～A2和B0～B2均为拟合系数。

然后由式(7)、式(8)分别计算θ、Cp对拟合变量T的导数，将Darcy系数R写为拟合变量T的函数形式：

(9)

最后将R代入Q的定义(式(2))中，得到斜孔壁特征参数Q随拟合变量T，即Ma或CL的变化。

3 空风洞状态试验结果

空风洞流动特性测量试验Ma=0.50～0.95，图2给出了斜孔壁不同流向位置XP处气流偏角和压力系数随Ma的变化规律，并给出了按照2.3节方法处理后的拟合结果，图例中L为试验段长度。结果表明，拟合结果与试验结果吻合度良好，偏差量随着Ma增大而降低，除个别跳点外，试验值与拟合结果偏差小于10.0%；气流偏角对来流马赫数的拟合度高于90.0%，压力系数拟合度高于95.0%。因此，拟合结果可以准确还原斜孔壁流动特征，能够替代试验结果进行微分计算。同时，气流偏角和压力系数随Ma变化呈明显的规律性：

图2 马赫数对孔壁流动的影响Fig.2 Influence of Mach number on perforated wall flow

1)θ随Ma的增大而线性减小，即由试验段向驻室方向的出流逐渐增强。试验范围内，模型区位置(XP=0.45L)变化量约为0.4°，加速区(XP=0.12L)和支架区(XP=0.65L)变化量接近1°。

2)Cp随Ma增大呈抛物线变化，Ma<0.75范围内变化较平缓，而Ma>0.75后量值迅速增大；该规律与气流偏角是对应的，出流增强需要更高的压差来维持。

根据试验结果，空风洞状态斜孔壁流动表现出以下两个明显的特征：

1) 差阻性。除Ma=0.95外，Cp均为负值，即试验段侧压力低于驻室侧压力，而穿孔流动仍以出流为主，即负压差时驻室内低能气流也很难克服动压头进入试验段。差阻性是斜孔壁的优势，能够降低入流与主气流混合时导致的不均匀流动。

2) 非线性。θ与Cp之间存在非线性关联，二者随Ma增大分别呈一次和二次变化，因此θ-Cp特征曲线的斜率，即R必然随着Ma变化。

采用2.5节差量法计算了3个流向位置斜孔壁Q系数随Ma的变化，结果如图3所示。可以看出，随着Ma的增大，孔壁特性参数Q值逐渐减小，模型区的量值及变化规律与加速区、支架区差异明显：

1)XP=0.12L和0.65L处，Q系数随Ma增大而迅速降低，从低亚声速的接近1.0降低至Ma=0.95时的0.1左右，即斜孔壁流动特性从开口边界向实壁发展。

图3 马赫数对孔壁特性参数Q的影响Fig.3 Influence of Mach number on porosity parameter Q of perforated wall

2) 在模型区XP=0.45L处，Ma<0.80范围内Q值随Ma变化较小，斜孔壁流动特性近似满足线性假设；而Ma>0.80的跨声速范围内，Q值随Ma增大而减小，但变化范围和量值均远小于加速区和支架区。

以上结果表明，基于均匀直孔的经典线性理论并不适用于斜孔壁，加速区和支架区由于穿孔流动未完全发展，Q值随Ma变化较大；而对试验数据干扰最大的模型区孔壁流动，在跨声速范围内也明显偏离了线性模型。

4 模型升力的影响

利用GBM-04A标模纵向测力结果评估模型升力对斜孔壁流动特性的影响。试验Ma为0.60、 0.85和0.95，七孔探针安装于上壁板XP=0.45L处，位于标模机翼上前方，为扰动最大的区域。图4给出了气流偏角和压力系数随模型升力系数的变化。

与空风洞结果相比，安装模型后上壁板XP=

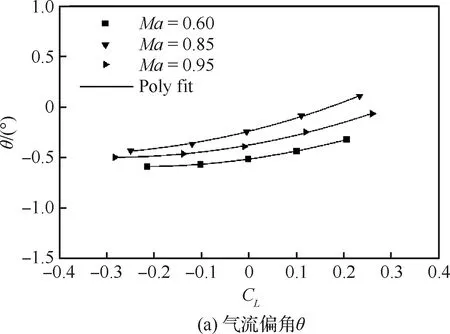
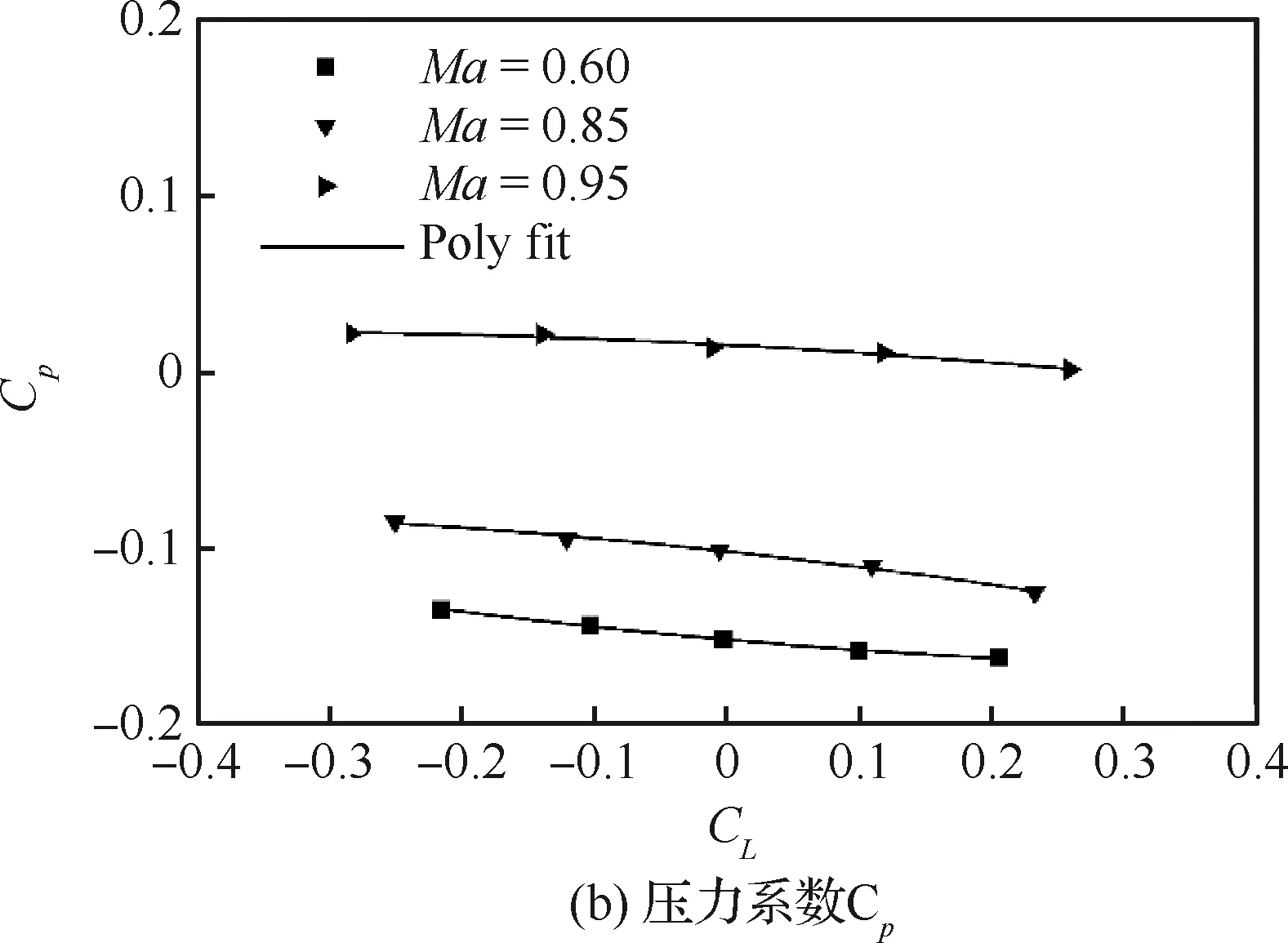
图4 模型升力对孔壁流动的影响(XP=0.45L)Fig.4 Influence of model lift on perforated wall flow (XP=0.45L)

0.45L处的流动特性发生较大变化：

1) 模型使测试位置斜孔壁流动向入流方向发展，Ma越高，引起的入流越强；压力系数变化较小，量值与空风洞状态较接近。

2)θ随模型CL增大呈抛物线趋势，变化量值约为0.5°；Cp随CL增大而线性减小，试验范围内变化幅度约为0.025。

模型机翼产生正升力时，上翼面为负压，上方的近壁区域气流变得稀薄，压力降低，诱导驻室向试验段方向的入流增强，因此导致气流偏角增大，压力系数降低。同时，入流增强还导致当地边界层厚度增大，由于探针位于边界层内部，因此与空风洞状态相比，压力变化相对较小。

根据微分法计算斜孔壁特性参数Q随模型升力系数CL的变化情况，结果如图5所示。可以看出：

1) 上翼面负压导致边界层变厚，对应的斜孔壁特性趋于开口边界，Q值随升力系数逐渐增大。

2) 模型升力的影响随着Ma增大而降低，Ma=0.60时，Q值随CL线性增大，而Ma=0.85、 0.95的跨声速范围内，Q值变化较平缓。主要原因是跨声速时升力面绕流前传影响降低，负压影响减小。

图6给出了零升力时斜孔壁Q值随Ma的变化，图中还给出了Neiland经验公式计算结果，以及1.2 m跨超声速风洞直孔壁早期比较测量法结果。可以看出，对于均匀分布的直孔壁板，Neiland经验公式结果与比较测量法结果规律一致，而Q量值略大，更接近开口边界。但对于当前的斜孔壁，经验公式已经失效，公式中未考虑开孔角度对孔壁特性参数的影响，工程中用于斜孔壁洞壁干扰修正时会带来较大的误差。

图5 模型升力对孔壁特性参数Q的影响(XP=0.45L)Fig.5 Influence of model lift on porosity parameter Q of perforated wall (XP=0.45L)

图6 几种孔壁特性参数Q的对比(CL=0)Fig.6 Comparison of porosity parameter Q in several perforated walls (CL=0)

5 结 论

利用七孔探针开展了斜孔壁流动特性测量试验，分析了斜孔壁流动的差阻性和非线性特征，获得了马赫数、模型升力的影响，基于微分法计算了斜孔壁特性参数。

1) 采用的试验测量方法和数据处理方法准确可行，可以用于国内斜孔壁流动特性的分析和参数测量中。

2) 与直孔壁相比，斜孔壁流动体现出明显的差阻性和非线性，空风洞以出流为主，随Ma增大而趋于实壁，有模型时随CL增大而趋于开口边界。

3) 对于斜孔壁，经典的Neiland公式失效，无法用于洞壁干扰评估和修正中。

致 谢

衷心感谢中国空气动力研究与发展中心高速空气动力研究所陈植工程师、杨可工程师在七孔探针校准和测试中提供的帮助。