基于流场/声爆耦合伴随方程的超声速公务机声爆优化

黄江涛，张绎典，高正红，余婧，周铸，余雷

1.中国空气动力研究与发展中心，绵阳 621000 2.西北工业大学 航空学院，西安 710072

随着气动设计技术、新能源技术的发展和未来市场需要，在各国民航对超声速声爆问题严格限制的条件下，民航业界普遍认为，发展小型超声速公务机的技术条件以及市场时机已经基本成熟。至少在未来的几年内，小型超声速公务机的研制、试飞将会被提上日程，实际上美国、俄罗斯、法国以及日本等国家的航空公司均已经推出一系列50座以下的超声速公务机设计方案，并提出了三代超声速民机的技术要求[1-2]，例如湾流Boom、Aerion、Spike等公司，并进一步制造出了缩比原型机进行拓展试验[3-5]。

超声速公务机面临的最大挑战之一就是民航对其超声速飞行时声爆水平的严格限制，声爆强度水平的影响因素主要包含了质量、飞行高度、飞行速度等。在总体方案选型以及布局优化过程中，计算流体力学以及相应的优化设计手段起着至关重要的作用，大幅度降低了设计成本。先进超声速公务机在气动性能上最明显的特点是高巡航效率、低声爆，需要在保证工程约束条件下，充分挖掘气动外形的升阻比、声爆设计潜力，是典型的多目标精细化设计问题，这对气动外形的综合设计方法提出了苛刻要求，传统的优化将面临计算量庞大、维度障碍等瓶颈问题。此时基于伴随方程的梯度优化是较为合理的选择。

国外在气动声爆优化方面的起步较早，主要研究工作包含了梯度、非梯度优化，大部分研究工作基于伴随方程的梯度优化进行，基于伴随方程的优化分为两个方向：近场声压变分伴随与流场/声爆伴随方程，最具有代表性是，Jameson等基于近场变分形式进行气动力/声爆优化[6]， Rallabhandi基于声爆预测方程耦合变分进行超声速飞机声爆优化[7]。国内在声爆预测、优化设计方面也开展了研究，取得了一定的进展，但大多工作基于进化算法以及波形参数方法等进行[8-10]，基于伴随系统的可微型声爆信号优化上的研究较少。基于伴随方法的优化设计尽管在全局性优化问题上存在不足，但在高维设计变量精细化优化问题上具有传统方法不具备的天然优势，由于伴随系统具有计算代价小、梯度计算量与各个学科设计变量个数均无关等优点，因此，在气动/声爆综合优化领域具有不可替代的优势，是一个值得发展的研究方向。

在地面声爆信号设计中，尽管近场变分实现方式比较简单，却无法直接设计地面声爆信号的形态，不利于声爆信号上升时间、过压峰值等综合特征的有效抑制。因此，本文基于中国空气动力研究与发展中心自主研发的大型并行结构化网格RANS(Reynolds-Averaged Navier-Stokes)求解器PMB3D、并行化伴随方程求解器PADJ3D以及声爆预测软件，在地面过压分布目标函数变分条件下，构建了耦合伴随优化系统，开展了求解过程中关键环节的变分与装配方法研究，并将进一步应用于超声速公务机声爆优化设计。

1 优化系统中的学科分析模块

1.1 并行化CFD求解器PMB3D

PMB3D是中国空气动力研究与发展中心自主研发的大型并行CFD代码，可求解任意曲线坐标系下的Navier-Stokes方程实现流场精细化数值模拟：

(1)

PMB3D求解器具备S-A (Spalart-Allmaras)一方程、剪切应力输运(SST)两方程湍流模型以及Langtry-Menter转捩预测模型，具备JST (Jameson-Schmidt-Turkel)、Roe、Vanleer等空间离散方法，具备MUSCL(Monotonic Upwind centered Scheme for Conservation Laws)迎风插值与WENO(Weighted Essentially Non-Oscillatory)格式，可实现LU-SGS隐式时间推进，支持FAS(Full Approximation Scheme)形式多重网格技术、多块对接、拼接以及重叠网格技术，以及具备基于MPI(Message-Passing-Interface)通信协议的大规模并行计算能力，广泛应用于常规气动力计算、多体分离、空中加油安全性分析、进排气系统、旋转部件气动特性计算以及火箭发射、级间分离等领域[11]。

1.2 基于Burgers方程的地面声爆预测

在进行地面声爆预测时，传统的直接利用CFD计算的方法带来网格耗散、网格需求量大、不适用于工程快速设计要求以及无法模拟大气分层特性等问题，因此，选择合理的声爆预测方程是评估设计结果的重要环节。目前用于预测地面声爆信号的方法主要包含波形参数法与Burgers方程，两者在声爆预测中具有良好的表现。但波形参数法[12-13]存在无法预测激波上升时间、预测信号存在间断导致声爆信号不可微等问题，无法进行快速傅里叶变换(FFT)和感觉噪声级分析，且在梯度优化体系中应用受限。因此，文中基于Burgers方程进行声爆预测[14-15]：

(2)

在时间步长足够小的前提下，可以通过算子分裂法对式(3)右端各项所代表的非线性项、吸收影响、分子松弛、射线管扩张以及大气分层项进行求解：

(3)

(4)

式(2)～式(4)中各参数的具体含义参见文献[14]。

图1～图3为课题组优化软件的CFD模块、Burgers方程声爆预测模块[16]对双圆锥、1021标模声爆[17-18]的预测与风洞试验以及NASA计算结果的对比，图中：δP、t、H/L分别为过压、时间和声爆预测位置坐标。可以看出，用于优化的声爆预测模块精度较高，为声爆伴随方程及优化提供了基础平台。

图1 双圆锥压力云图Fig.1 Pressure contour of cone

图2 声压计算与试验数据对比Fig.2 Comparison of sound pressure calculation and experiment data

图3 NASA1021标模声爆预测对比Fig.3 Sonic boom prediction comparison of NASA1021 standard model

2 基于流场/声爆耦合伴随思想的梯度计算

2.1 流场伴随方程求解梯度

简单回顾一下伴随方程的推导，对于目标函数最小化问题：

(5)

在流场收敛解的条件下，残差约束R(W,X,D)=0,W、X、D分别代表流场守恒变量、网格变量、设计变量。引入拉格朗日算子Λ可以构造以下目标函数：

L=I+ΛTR

(6)

式中：L为声爆目标函数。

对式(6)进行求导，有

(7)

(8)

式(8)就是流场伴随方程，通过隐式迭代方法求解Λ之后，可以通过式(9)和式(10)进行目标函数梯度信息求解。

(9)

(10)

最小化问题中的目标函数既可以是气动力，也可以是声压、总压恢复系数、流量、压比等参数，由以上推导过程可以看出，对于伴随方程来讲，不同的目标函数只需要改变伴随方程右端的变分项。其中目标函数I可以是升力、阻力、力矩、流量、压比等参数，R为残差约束，Λ为拉格朗日算子。

本文采用二阶精度的中心格式、人工黏性以及SST两方程湍流模型，采用手工推导方式进行黏性离散伴随方程构造，最终表达式为

Rc(λ)j,k,l-RD(λ)j,k,l-Rv(λ)j,k,l=0

(11)

式中：Vj,k,l、Rc(λ)j,k,l、RD(λ)j,k,l、Rv(λ)j,k,l分别代表网格体积、伴随方程的对流项、人工黏性项以及物理黏性项，对式(11)的迭代求解，文中采用了LU-SGS方法隐式时间推进方法，其中，离散伴随方程的边界条件采用矩阵形式处理方式，黏性项采用薄层近似，离散伴随方程求解时，并行机制依然采用单元数衡量的负载平衡、对等式计算以及MPI消息传递模式。本文求解器采用了多块对接网格技术，MPI传递的信息是各个进程中分割面上的两层虚网格上的伴随变量信息，详细推导可以参考文献[19]。

2.2 声爆伴随方程求解梯度

对于声爆设计，可以对地面声爆强度进行变分，也可以对近场声压进行变分。近场变分[6]实现方式更为简单，但无法直接设计地面声爆信号特征，因此，本文采用了地面变分形式，该方法需要推导声爆预测伴随方程，求解地面声爆目标函数对近场声压的梯度。声爆伴随方程的具体形式如下，详细推导可以参考文献[7]：

(12)

式中：λ、β、γ为中间伴随变量；Ib为地面声爆目标函数；A、B与A2、B2分别对应氮气、氧气分子弛豫矩阵；A3、B3为吸收过程矩阵。与声爆预测方程不同，式(12)的求解过程是声传播的一个反向过程，利用最终的伴随变量可以很方便地获取地面声爆目标函数对近场声压的梯度：

(13)

式中：pin为均匀坐标系下的过压分布。需要注意的是，式(13)求解的是地面声爆目标函数对均匀坐标系下的近场输入声压的梯度，向网格单元装配需要将该梯度转化为CFD网格非均匀坐标系下，依据网格非均匀坐标系与声爆均匀坐标系的转换关系，可以方便推导出对角稀疏化的坐标转换雅克比矩阵χ[7]，依据分段线性插值表达式可以实现均匀坐标系与非均匀坐标系的导数转换：

(14)

图4和图5给出了基于声爆伴随方程中间伴随变量的分布，以及地面声爆目标函数对近场非均匀坐标系下声压的梯度验证，地面声爆目标函

图4 不同高度(H)声爆伴随变量Fig.4 Adjoint variables of sonic boom at different altitudes (H)

图5 声爆伴随梯度与差分对比Fig.5 Comparison of gradients of sonic boom adjoint and finite difference method

数采用以下形式：

式中：pT为声爆设计目标特征。可以看出声爆伴随方程梯度计算结果与差分结果较为一致，可以为耦合伴随系统提供准确的地面声爆目标函数对近场声压的梯度。

2.3 流场/声爆耦合伴随方程

Rallabhandi在文献[7]中采用非结构网格求解器FUN3D进行声爆优化，由于非结构的不规则性以及采用了自适应网格产生的拉伸影响，需要将网格格点单元的流场变量向同高度坐标变换，因此，近场声压函数关系式是关于流场变量与网格坐标的函数，雅克比矩阵χ就包含了对网格坐标X的变分。

为简化耦合伴随系统的变分推导过程，降低变分难度，文中依据结构网格拓扑的可控性，进行以下操作规定：① 在近场过压提取站位附近将网格单元分布划分为规整格式，即高度、宽度方向均为直线，这样近场过压分布就不需要向同高度转换；② 非均匀坐标下沿X方向各个站位初始过压的提取均从本单元选取。由上述规则，近场过压的提取基本消除对X的依赖，雅克比矩阵χ不再包含对网格坐标X的变分，且仅与自身单元守恒变量W相关,即

p0=T(W)

(15)

式(15)大幅度简化了近场声压雅克比转换矩阵的变分难度。与文献[7]不同，本文进行变分的约束没有网格伴随方程的残差项，而只有流场残差R=0与对声压转换关系(p0-T)=0，基于上述原则，下面给出耦合伴随的推导过程，将声爆目标函数引入流场以及声爆拉格朗日算子λf、λb：

(16)

对式(16)进行变分展开：

(17)

综合文中网格划分以及近场声压提取原则，可以看出式(17)右端第1、第6项为零，变分表达式为

(18)

(19)

(20)

3 并行环境下近场声压提取与变分结果装配

耦合伴随方程的第1步是为声爆传播方程提供近场声压输入，在该问题上面临的主要关键技术是并行环境下提取多块网格运算中的进程号、网格块编号以及单元编号。

为方便近场声压的提取，定义长方体“盒子”，该盒子由长方体两个角点定义，用于方便选定近场网格单元，避免繁琐的人工操作，如图6所示。

图6 并行环境下的网格分布与“声压盒”Fig.6 Grid distribution and “sound pressure box” in parallel environment

进程号、网格块编号和单元编号提取、声爆预测以及变分结果装配过程如下：

1) 各个进程的网格判断是否有格心坐标处于盒子内，若有，记录该进程的编号。

2) 记录该网格块在当前进程中的编号。

3) 记录格心在当前网格中的编号及X坐标。

4) 主进程将各个进程的编号、坐标文件收集写出，并将过压按X顺序进行排列输出近场文件。

5) 声爆预测迭代推进计算。

6) 声爆伴随方程反向迭代推进求解。

7) 转换为CFD坐标系。

8) 按编号、坐标文件将变分结果按对应的进程编号输出，向各个进程装配。

9) 流场伴随方程求解。

4 声爆优化设计体系

本文的研究工作基于课题组自主研发的优化设计软件AMDEsign进行，AMDEsign是面向航空航天飞行器气动外形多学科优化研发的分布式优化软件，集成了气动、气动/结构、气动/隐身多目标多学科设计体系，具有进化算法/代理模型、耦合伴随等模块，适用于不同设计问题的各种优化模型、参数化方法、网格变形技术以及学科分析。

本文发展的低声爆超声速公务机优化技术属于AMDEsign中的耦合伴随模块，其中CFD方法采用中心格式、SST两方程湍流模型、多重网格加速收敛以及大规模并行计算；梯度求解采用对应的并行化伴随方程与梯度求解器；参数化方法采用基于NURBS基函数的自由变形技术(FFD)[20]；变形网格采用并行化RBF_TFI[21]，声爆优化基本流程如图7所示。

图7 流场/声爆耦合伴随优化流程Fig.7 Flowchart of flow field/sonic boom coupled adjoint optimization

5 典型超声速公务机声爆优化

基于巡航马赫数为1.5的小型超声速公务机的基本构型，开展超声速巡航状态下的声爆优化设计研究。

其优化数学模型为

Constraints:

主要部件包含机翼、机身以及立尾。网格划分为239块，半模网格规模为900万量级，为比较准确地捕捉空间激波形态，空间网格拓扑按照马赫角进行x方向拉伸且对下表面进行加密，如图8 所示。采用64核进行并行计算。

图9给出了基于NURBS基函数的自由式变形参数化示意图，共采用60个控制顶点实现机身、机翼气动外形参数化建模；设计变量为图9中x方向4～6个截面，以及机翼展向4个截面，近场“包围盒”处于机身下方60 m处。图10为初始外形的对称面压力云图，可以看出按照马赫角拉伸的网格拓扑能够较为清晰地捕捉空间激波形态。

图8 CFD网格分布Fig.8 Distribution of CFD grid

图9 自由式变形参数化Fig.9 Parametric lattice of free form deformation

图10 初始外形巡航状态压力云图Fig.10 Pressure contour of initial configuration in cruise state

图11给出了耦合伴随系统的收敛历程，图12和图13分别给出了y=0与x=8站位截面耦合伴随方程的第1伴随变量云图，云图呈反向传播，实际上，结合最终的导数计算式(9)，可以从伴随变量云图分布上定性看出流动敏感性区域。同样，结合耦合伴随变量云图分布以及伴随方程耦合变分项的装配位置可以看出，随着伪时间推进迭代，由空间近场向物面“传播”，因此，耦合伴随方程呈现先收敛，进而阶段振荡，最终完全收敛的特征。

图14给出了地面声爆目标函数优化过程，经过9代优化，声爆抑制效果逐渐收敛，图15给出了地面声爆目标函数对近场声压的梯度优化前后对比，图16给出了优化前后地面过压对比。可以看出，伴随优化效果较为明显，第2道激波的峰值明显降低。由于机头的控制点没有作为设计变量，第1道激波压力峰值抑制以及激波上升时间控制效果不太明显。

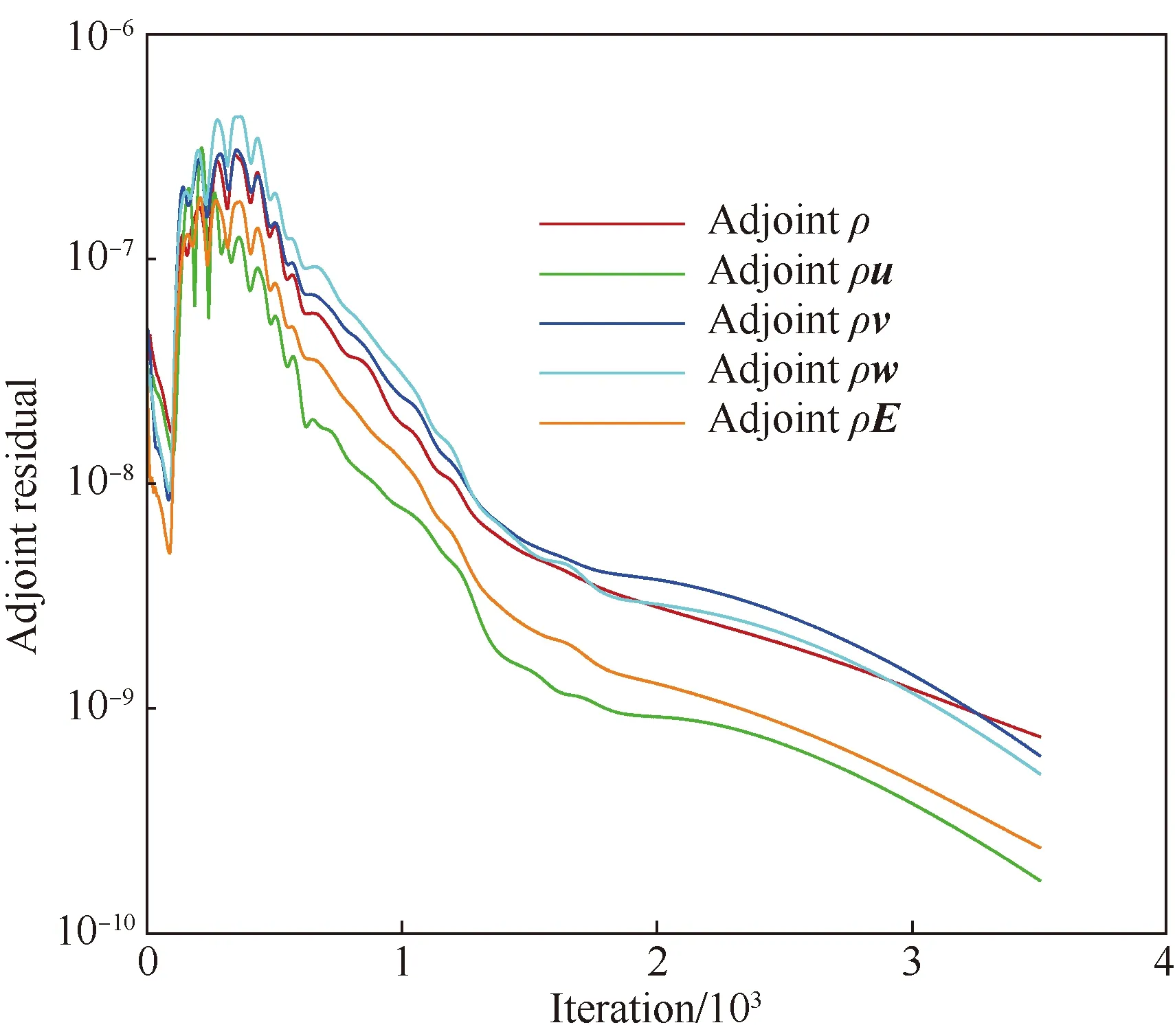
图11 耦合伴随系统收敛历程Fig.11 Convergence history of coupled adjoint system

图12 耦合伴随方程第1伴随变量云图(y=0)Fig.12 First adjoint variable contour of coupled adjoint equations (y=0)

图13 耦合伴随方程第1伴随变量云图(x=8)Fig.13 First adjoint variable contour of coupled adjoint equations (x=8)

图14 目标函数优化收敛历程Fig.14 Convergence history of objective function optimization

图15 地面信号对近场声压梯度的优化前后对比Fig.15 Comparison of gradient of ground signal with near field sound pressure between initial and optimized configuration

图17给出了优化前后感觉噪声级的频谱特性，横坐标为1/3倍频程频段，纵坐标为响度级。由于频谱特性峰值与激波上升时间密切相关，而第1道激波上升时间与机头形状关系密切，如前面所述，文中没有将机头作为设计变量，图16第1 道激波上升时间变化不大，因此，峰值变化不大，但在整个频段内，感觉噪声级幅值得到有效抑制，从而起到降爆作用，验证了文中耦合伴随优化方法的有效性。

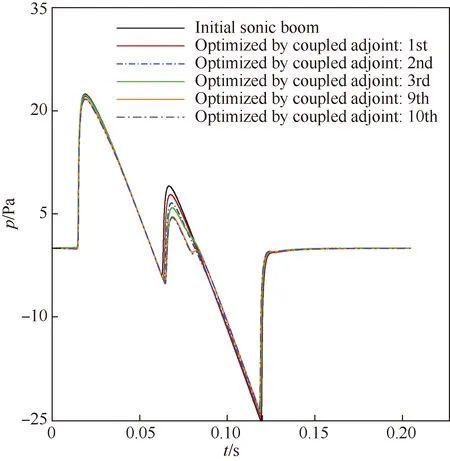
图16 地面过压优化过程Fig.16 Optimization process of ground pressure

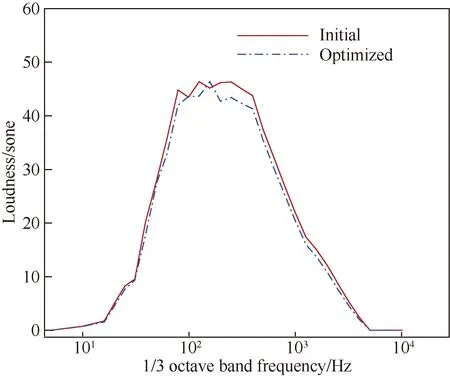
图17 优化前后感觉噪声级频谱特性Fig.17 Characteristics of spectrum on perceived noise level of initial and optimized configuration

6 结 论

基于并行化结构网格RANS求解器PMB3D以及伴随方程求解器PADJ3D，结合增广Burgers声爆预测与伴随方程，开展了流场/声爆耦合伴随方程构造、求解方法以及声爆优化研究。

1) 文中提出的“包围盒”、单元定位以及排序方法，大幅度提高了并行环境下CFD数值模拟结果的近场过压分布提取效率，避免了繁琐的人工操作。提出的并行环境下目标函数变分结果向耦合伴随方程对应的网格单元装配方式简单有效。

3) 文中构建的声爆模块计算精度较高，伴随模块计算的地面声爆目标函数对近场声压的梯度与有限差分结果较为一致；优化测试算例表明，耦合伴随系统具有较高的优化设计效率，地面过压优化效果比较明显。

本文基于结构网格求解器，开展了流场/声爆耦合伴随优化方法研究，验证了文中提出的插值、变分原则的有效性，为气动力、声爆综合一体化设计提供了研究基础。在此基础之上，将进一步基于高效的耦合伴随系统开展气动力/声爆综合设计以及声爆抑制原则等研究。