小振幅振动翼型升力迟滞环变向的成因分析

薛臣，周洲,*，李旭，许晓平

1.西北工业大学 航空学院，西安 710072 2.西北工业大学 无人机特种技术重点实验室，西安 710065

随着航空技术的发展，飞行器的应用范围变得越来越广泛，因此面临的问题也更加复杂。近几年，人们越来越重视绿色航空，太阳能无人机由于其自身独有的特点越来越受到人们的重视，如美国的太阳神[1-3]、英国的西风[4-5]。此外，谷歌和Facebook也都宣布了各自的太阳能无人机计划。太阳能无人机因为受限于目前能源利用率较低的因素，一般展弦比很大，呈现超轻面密度的结构特点，所以太阳能无人机在飞行中会面临较严重的振动问题，研究这一问题对指导太阳能无人机设计有重要意义。

在翼型振动方面，目前多数学者的研究重点都在大迎角运动和增升机理方面。大迎角俯仰振荡研究方面现在主要集中在翼型动态失速研究，Albertson等[6]、Helin和Walker[7]通过实验发现翼型前缘加速侧会出现动态失速涡(文献[8-9]中也叫前缘涡)，在低雷诺数条件下，这个涡会显著提高升力。文献[10-11]也指出对于扑翼来说，这个动态失速涡会在增升方面扮演着重要的角色；Leknys等[12]采用粒子图像测速(PIV)对NACA0021翼型的动态失速问题进行研究，发现翼型的转动造成了翼型的升力有一个明显的延迟现象，而且可以将翼型的整体分离流动出现的角度推迟到60°。

注意到在翼型的大幅振荡研究中，已经发现翼型的振动会推迟翼型的失速迎角，这种由翼型振动带来的迟滞现象也吸引了很多学者的注意。实际上，这种非定常效应引起的迟滞效应与很多因素有关，例如振动频率，振动轴位置和振动幅度等[13]，Jung和Park[14]发现在低雷诺数条件下，振动减缩频率的增大会减小尾涡的脱落频率； Yu等[15]研究了前缘涡对翼型的升力阻力和力矩系数的影响，发现随着减缩频率k的增大，翼型的最大升力系数和相应迎角逐渐增大。Qin等[16]在低雷诺数情况下通过大涡模拟计算了不同减缩频率下的SD7003翼型的气动特性，发现减缩频率k的增大会使升力系数随时间变化(CL-t)曲线的相位变大；Yu和Bernal[17]发现在相同的减缩频率情况下，振动轴位置的后移会延迟翼型周围涡的发展，但是主要的流动结构并没有改变。

而在小振幅振动研究中，目前所见的研究并不多，高正红[13]在无黏跨声速条件下，研究了振动轴位置和减缩频率对小振幅振动翼型气动特性的影响，研究发现小振幅简谐振动翼型的升力系数-迎角(CL-α)曲线会呈现一个椭圆状的环型曲线，指出减缩频率的变大会使得CL-α曲线的绕向从逆时针变为顺时针，而且当振动轴位置后移时，发生这种变向所对应的减缩频率k值越大；Ekaterinaris和Platzer[18]利用面元法计算了NACA0012翼型的强迫振动，迎角幅度为±10°(未失速)，发现翼型振动会带来相位上的改变，而且减缩频率k的增大会使得力矩系数迟滞环从逆时针变为顺时针。

虽然已经有不少学者研究了翼型振动带来的一些特殊现象，但是这其中仍有很多问题并没有得到很好的解释，目前大多学者都把迟滞环方向的改变简单归结为非定常效应引起的，张正秋等[19]指出，升力与扭矩的迟滞效应随各参数的变化趋势相同，但是从文献[13]的计算结果可以看出，升力系数迟滞环的变化和力矩系数迟滞环的变化是不相同的，并且文献[20]中指出“非失速情况下，气动力系数的迟滞环面积表征了迟滞效应的大小”，注意到文献[20]是在力矩系数变化情况下得到的结论，这一结论是否能推广到升力系数迟滞环还有待研究。

可以看出目前专门针对翼型小振幅振动问题展开研究的并不是很多，而且多基于跨声速情况，会有激波出现，对于低速情况，这种翼型小振幅振动会不会出现类似文献[13]里的情况，有待研究。本文在前人的基础上，结合本课题组在太阳能无人机实际飞行中遇到的特定问题，在低雷诺数条件下，从翼型小振幅振动入手研究振动轴位置和减缩频率对振动翼型的气动特性影响。

1 计算模型

本文采用的翼型为常用的低雷诺数翼型SD7037，网格划分如图1所示。Menter[21]指出，为准确地捕捉层流和转捩边界层，在低雷诺数流动计算中，需使y+接近于1。本文采用结构化的O型二维网格，翼型弦长为c，计算域边界半径为25c，整个计算域及壁面附近网格如图1所示。

图1 振动翼型的计算网格Fig.1 Calculation grid of oscillation airfoil

2 数值方法

当弦长雷诺数在2×105～1×106的范围内变化时,基于雷诺时均的Navier-Stokes(RANS)方程也可以较好反映出翼型周围的流场结构[18,22]。本文采用滑移网格方法实现翼型的振动，采用k-kl-ω转捩模型，因为S-A(Spalart-Allmaras)及SST(Shear Stress Transport)k-ω湍流模型主要考虑的是全湍区域，很难预测低雷诺数下的分离泡结构，而k-kl-ω转捩模型可以相对准确地捕捉观察到翼型表面复杂流动现象及特征，转捩位置及分离泡预测能力及精度相对较高，在低雷诺数转捩流动数值求解中适用性较好[23]。

为了验证本文所用转捩模型的准确性，采用算例1的实验数据[24]，验证了k-kl-ω转捩模型捕捉低雷诺数分离泡特征的能力，结果如图2所示(图中Cp为压力系数)。

算例1：翼型GA(W)-1，雷诺数Re=1.6×105，迎角α=12°。

本文中翼型的运动规律定义为

α=αmsin(ωt)

(1)

式中:αm为迎角运动幅度，本文中取为4°;ω为运动圆频率，与减缩频率k的关系为

(2)

其中：U∞为来流速度。

为了加快收敛，本文先利用定常计算得到一个较为稳定的流场作为非定常运动计算的初始输入，继续进行非定常运动计算，每个时间步内的子迭代步数选为30，时间步长按无量纲时间t/T=0.004 5选取，其中T为翼型运动周期。

为了验证本文采用的计算方法对非定常运动计算的可靠性，采用了2个算例来验证。

算例2：利用Piziali[25]的实验结果进行验证，翼型为NACA0015，马赫数Ma=0.29，Re=1.95×106，运动规律为α=4°+4.2°sin(2πft)，其中频率f=10 Hz。

图2 GA(W)-1翼型压力分布(α=12°)Fig.2 Pressure distribution of GA (W)-1 airfoil (α=12°)

算例3：翼型为NACA0012，Re=485 755，Ma=0.035 5，运动规律为α=10°+10°sin(2πft)，其中f=1.62 Hz，实验条件及数据可以参考文献[26]。

从图3和图4给出的升力系数迟滞环曲线中可以看出，本文采用的方法与实验结果符合较好，说明本文采用的计算方法有足够的可靠性。

图3 NACA0015翼型升力系数迟滞环Fig.3 Hysteresis loop of lift coefficient of NACA0015 airfoil

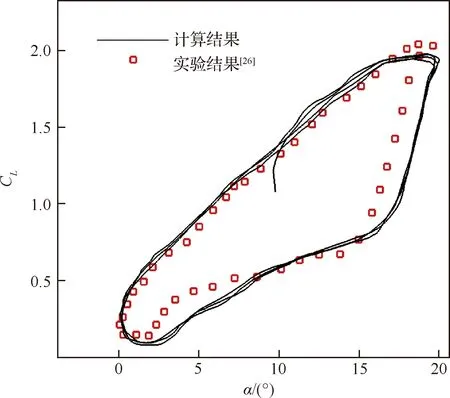
图4 NACA0012翼型升力系数迟滞环Fig.4 Hysteresis loop of lift coefficient of NACA0012 airfoil

3 结果及讨论

通过计算可以发现，当翼型作俯仰振动时，CL-α曲线呈现为一个椭圆形，而且方向上也有变化。为了研究振动轴位置和减缩频率k对CL-α曲线迟滞环的绕向的影响，本文首先在减缩频率不变的情况下，研究振动轴位置对迟滞环的影响，随后通过更改减缩频率k，研究k对迟滞环绕向的影响，并分析原因。

3.1 振动轴的影响

本文中定义了2个坐标系，一个是随着平板运动的体坐标系oxy，另一个是固定的惯性系OXY(风轴系)，当翼型未振动时，这2个坐标系是重合的，如图5所示。分别将振动轴定位于前缘处、1/4弦线、半弦长、后缘处，即x=0,0.25c,0.50c,c处(见图5)。

这里仅展现k=0.3和k=1.0时的计算结果分别如图6和图7所示。从图6(a)可以看出，当k=0.3，翼型绕前缘转动时，此时的CL-α曲线“迟滞环”的绕向为顺时针，对比图6(d)可以发现此时的“迟滞环”方向变为逆时针，即在k保持不变的情况下，当振动轴向后移动时，“迟滞环”方向有从顺时针方向变为逆时针的趋势，而且在这个变化过程中，会经历一个“直线”过程，如图6(c)所示。当k=1.0时，可以看出当振动轴从前缘移动到半弦长处时，对应的迟滞环均为顺时针，但是当振动轴移动到后缘处时，CL-α曲线此时也出现了近似直线的情况，如图7(d)所示。

图5 不同振动轴在坐标系中的示意图Fig.5 Sketch of different pivot locations in coordinate system

为了弄清楚这种现象的原因，将升力系数随时间变化曲线展开，如图8所示。从图中可以看出k=0.3，振动轴位置从前缘向后移动时，升力系数的峰(谷)值在时间上均出现了向后移动。

表1给出了不同雷诺数下对应不同振动位置的升力系数曲线特性，表1中的Δt和φ是相对于α-t曲线计算得到的时间差和相位差，负值代表相位相对α-t曲线(时间)延迟，正值代表相位提前；CLmax和CLmin分别为升力系数的最大值和最小值，CLamp为振动时升力系数的幅值大小，CLmean为

图6 k=0.3时不同振动位置的CL-α曲线(Re=7.89×105)Fig.6 CL-α curves at different pivot locations at k=0.3 (Re=7.89×105)

图7 k=1.0时不同振动位置的CL-α曲线(Re=7.89×105)Fig.7 CL-α curves at different pivot locations at k=1.0 (Re=7.89×105)

图8 k=0.3时不同振动位置的CL-t曲线(Re=7.89×105)Fig.8 CL-t curves at different pivot locations at k=0.3 (Re=7.89×105)

升力系数的平均值。从表1中可以看出，振动轴的位置对升力的平均值影响不大，而且振动轴的位置越靠近后缘，升力系数能达到的最大值越小；对于同一振动轴位置，随着雷诺数的变大，时间和相位在数值上是逐渐增大的，虽然对于x=c位置来说，相位为负值，代表此时CL-t曲线相对于α-t曲线相位滞后，但是随着雷诺数的增大，其滞后相位的绝对值也在变小，即当雷诺数变大时，会使得相位提前变多。

此外，从表1中还可以看出Re=7.89×105时，x=0位置处的相位较迎角曲线的相位要提前19.22°，x=0.25c位置相位提前10.43°，而对于x=c位置，相位滞后11.52°,这种相位上的差别就导致了迟滞环曲线的方向变化，这里可以从数学上加以证明。

表1 不同雷诺数下对应不同振动位置的升力系数曲线特性(k=0.3)

迎角的运动形式为α(t)=αmsin(ωt)，稳定后的升力系数曲线可以写为：CL(t)=CLampsin(ωt+φ)，这点在3.2节可以被证明。

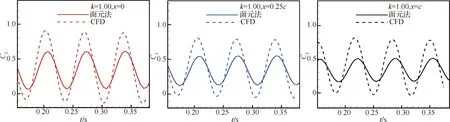
为了方便说明，以前1/4周期为例(其他情况类似)，t1(t1T/4)时刻刚好使得ωt2=θ2=π-θ1，此时α2=α1，有CL(t2)=CLampsin(ωt2+φ)=CLampsin(π-θ1+φ)，容易得到：φ>0°时，CL(t1)>CLamp(t2)，反映到CL-α曲线上，即为顺时针方向；φ<0°时，CL(t1)

从数学关系上的证明可以看出，在一定范围内，相位φ的绝对值越大，t1、t2时刻对应的升力系数差别越大，即迟滞环表现得会更加饱满(无论是顺时针还是逆时针)，而φ又与振动轴位置和k相关，所以这才是导致迟滞环变化的根本原因，而不是简单的增大k就会导致迟滞环饱满，对比图7(d)和图6(d)，可以看出增大k也可能使得迟滞环曲线变得扁平，甚至为直线；从图6和图7中还可以看出，向前移动振动轴位置也可能使得迟滞环变得更加饱满。

图9 相位差φ带来的升力系数差Fig.9 Lift coefficient difference caused by phase difference φ

从以上分析可以看出，当振动轴位置向后缘移动时，CL-t曲线的相位会变小，即出现相位延迟，CL-α曲线也会从顺时针向逆时针变化。对于此现象，可以有如下解释：以平板为例，振动轴位置定在离前缘d处，如图10所示。假设整个平板在来流速度为U∞的流场里以ω*的角速度绕振动轴顺时针旋转(即迎角增大)，则在体轴系里面观察，前缘处会有一个vLE=ω*d的向上速度，如图10所示，而当迎角为αoff时，此时在体轴系里观察来流，在y方向上的速度为vy=U∞sinαoff，但是注意到此时前缘自身仍有一个vLE的向上速度，所以前缘处感受到的实际速度只有vLE-real=U∞sinαoff-vLE，也就是说实际迎角被减小了，而且只有当αoff=arcsin(ω*d/U∞)≈ω*d/U∞(小角度)才能刚好抵消前缘运动速度的影响，此时在体轴系观察，来流沿x方向流过，迎角为0°，即相比较绕前缘振动，时间上滞后了。

这里虽然只对前缘处作了分析，但是其他位置处的有效迎角是相似的，在振动轴前的部分有效迎角是减小的，振动轴后处的部分有效迎角在增大，这也可以看出当d较大时，即振动轴离前缘的位置越远，有效迎角减小的部分更多，要达到和绕前缘振动相同状态则需要更长的时间，反映在升力系数上，就是振动轴的后移延迟了相位，如图8所示。此外，还可以看出振动轴带来的相位滞后在k一定的情况下，主要和离前缘的距离d和当地的平均流速Uav的比值近似呈线性关系。

图11中展现了翼型振动时沿X方向的速度vX云图，从图11中可以看出，当振动轴位于翼型后缘(x=c)时，基本上要比绕前缘处(x=0)振动滞后0.02 s，才会出现相似的流场结构。

图10 平板的速度示意图Fig.10 Sketch of velocity of flat plate

图11 绕前缘和后缘振动不同时刻的vX云图对比(k=0.3)Fig.11 Comparison of vX contour at different times when pivot located at leading edge and trailing edge (k=0.3)

3.2 减缩频率的影响

本节在相同振动轴位置，研究了不同k对迟滞环曲线的影响。图12给出了x=0，0.25c，c时，k=0.05,0.15,0.30,1.00的计算结果。

从图12中可以看到，在不同振动轴处，随着k的变大，“迟滞环”的转向会从逆时针向顺时针转变，中间会出现直线段过程，这并不如文献[19]结论中指出的那样，“随着振动频率的增加，气动力系数迟滞曲线饱满程度增加”。可以看出增大k值类似于振动轴的前移过程，也可以提前相位。

从图12中还可以看出，当k=1.00时，越靠近前缘处，升力系数迟滞环面积越大，这主要是因为当振动轴靠近前缘时，初始的负相位φ的绝对值较小，因此k增大到一个较小的值时，就会抵消这个负相位，此时升力系数迟滞环即变为直线型，继续增大k这个相位φ就会变成正值，并不断变大，按3.1节的解释，迟滞环面积会变大，且此时的升力系数迟滞环为顺时针转向，而当振动轴位置靠近后缘时，这个初始的滞后相位的绝对值会较大，因此k需要增大到更大的水平才能抵消这个滞后相位，所以反映到迟滞环曲线上，如图12，当k=1.00时，越靠近前缘的振动轴位置的曲线更加饱满，当振动轴位于后缘时，CL-α曲线基本呈直线型，表明当振动轴位于后缘时，当k增大到1.00时，才能抵消相位滞后，而当振动轴位于前缘时，k只需到0.15，就可以抵消相位的滞后了。

图13将不同k下的CL-t曲线与α-t曲线进行了对比，可以看出，随着k的变大，CL-t曲线相对于此时对应的α-t曲线的相位逐渐变大，即k的增大可以使得相位提前，此时对应的CL-α曲线迟滞环也会从逆时针向顺时针变化，直线段则对应相位差为0°的情况。

图12 不同振动轴位置随k变化的CL-α曲线(Re=7.89×105)Fig.12 Variation of CL-α curves with k at different pivot locations (Re=7.89×105)

图13 不同k的CL-t曲线与α-t曲线的对比(Re=7.89×105)Fig.13 Comparison between CL-t curves and α-t curves for different k (Re=7.89×105)

图14给出了φ随k的变化，可以清楚地看到对于同一振动轴，k的增大使得曲线的相位提前，而且曲线的相位是与减缩频率k和振动轴有关的，此外可以看出相位与k之间存在一个函数关系，这点也在后文中进行了证明。

图15给出了SD7037翼型在不同雷诺数下的小迎角升力系数曲线，可以看出在气动上，本文选取的翼型在小迎角范围内，升力系数和迎角近似呈线性关系CL=CLαα(CLα为升力线斜率)，现在将翼型及流场之间的共同作用看成一个系统，升力系数是输出量，很明显在小迎角范围内此时这个系统满足线性系统的定义，本质上是线性的。从控制的角度来看，一个系统的线性与否是其自身属性，与输入量没有关系，虽然这里的输入为迎角的变化：α=αmsin(ωt)，但是不会改变这个系统的线性特点，所以本文在这里将此系统看作是线性系统。另外从图8中也可以看出，升力系数CL此时也是正弦变化形式，而且频率保持与迎角变化频率一致，也从侧面验证了这种假设的合理性。在线性系统假设的前提下，输入(迎角)和输出(升力系数、力矩系数)的关系可证明如下。

图14 CL-t曲线与α-t曲线之间的相位差φ随k的变化Fig.14 Variation of phase shift φ between CL-t curve and α-t curve with k

图15 SD7037翼型在不同雷诺数下的小迎角升力系数曲线Fig.15 Lift coefficient curves of SD7037 airfoil at small angles of attack with different Reynolds numbers

系统的输入为α(t)=αmsin(ωt)，则输出的拉氏变换可以写为

CL(s)=Φ(s)αm(s)

(3)

式中：

Φ(s)为整个系统的传递函数；M(s)为Φ(s)的分子多项式；-s1,-s2,…,-sn为系统极点。为了方便讨论，不妨认为系统稳定，并假设特征根均为互异的负实根，利用部分分式展开法即有：

(4)

A2e-s2t+…+Ane-snt

(5)

当t趋于无穷时，输出稳态分量：

(6)

所以稳态分量为

CL(t)|t→∞=αm|Φ(jω)|·

αm|Φ(jω)|sin(ωt+∠Φ(jω))=

CLamp(ω)sin(ωt+φ(ω))

(7)

从证明中可以看出，振幅CLamp和相位φ都是与ω有关的函数，这也验证了图14所示的规律。

结合以上证明，如果小振幅振动的翼型可以被看成一个线性系统，则可做一个合理的假设，即当雷诺数和振动轴位置确定后，运动的初始相位不会影响最终的CL-t曲线的相位。为了验证这一假设，本文选取k=0.30、振动轴位置为x=0.25c和x=c处进行分析，从表1可以看出，振动轴位于0.25c处时，CL-t曲线相对α-t曲线的相位本身就是提前的，而振动轴位于后缘时，这个相位是负值，即相位滞后了。为了验证初始相位对最终CL-t曲线相位的影响，在x=0.25c处预加-18°的初始相位，即α=αmsin(ωt-18°)，相应的在x=c处预加+18°的初始相位，即α=αmsin(ωt+18°)。计算结果如表2所示，对比表1中的数据，可以发现初始相位的存在并没有改变最终的相位特性，即CL-t曲线的相位不受迎角的初始相位影响。

表2 改变初始相位后的CL-t曲线相位特性

Table 2 Phase characteristics ofCL-tcurve after changing initial phase

在3.1节的分析中，已清楚了振动轴位置主要是通过影响有效迎角进而影响相位的变化,接下来研究k的变化对相位的影响。

注意到本文研究的是翼型的简谐强迫振动，所以这里参考了二维Theodorsen非定常气动力模型，具体表达式[27-28]为

将本文的翼型运动规律带入化简，可以得到升力系数表达式：

CL=πkαm(cos(ωt)+aksin(ωt))+…+

(9)

参考文献[17,29]，本文在这里把翼型排开空气的质量称为“附加质量”，而且文献[17,29]的研究结果都指出：“当k较大时，翼型排开的空气质量带来的惯性反作用力会带来额外的升力，从而提前相位”,而且可以看出当k较大时，带来的额外升力也会比较明显。

从式(9)中还可以看出，这个附加质量带来的惯性反作用力只会对升力的幅值和相位有所影响，并不影响CL-t曲线的频率特性，这与计算结果也是相符合的。

此外，从图14中可以看出，当振动轴位置向后缘移动时，k增大带来的相位增加并不明显，即升力系数曲线的相位对k不再敏感了，这与文献[13] 的结论相似，从本节的分析可以看出，当k变大时，翼型排开的附加质量带来的惯性反作用力会变大，使得翼型升力变大。从式(9)可以得到在周期开始时(瞬时迎角为0°)，由于反作用力带来的升力系数增量为ΔCL=πkαm，所以当k=1.00 时，由于反作用力带来的升力系数增量ΔCL1-t=0.219 3，k=0.30时，升力系数增量ΔCL2-t=0.065 8，即k=1.00相比于k=0.30，升力系数差值为ΔCL-t=0.153 5，从图13中可以得到绕前缘振动时，k=1.00和k=0.30在周期开始时升力系数差值为ΔCL1-c=0.221 1，而绕后缘振动时，对应的升力系数差值ΔCL2-c=0.116 6，此时有ΔCL1-c>ΔCL-t>ΔCL2-c，可以看出当振动轴后移时，升力增量的确是减小的，这主要是因为当振动轴在前缘时，翼型在迎角增大的过程中，有效迎角也在变大，如图16(a)和图16(b)所示，即此时升力的2个组成部分，附加质量带来的反作用力和常规的气动力都是增加的，因此相位提前很显著，而当振动轴后移时，特别地，对于振动轴在后缘时，翼型上的有效迎角是减小的，如图16(c)和图16(d) 所示，虽然由于附加质量带来的反作用力随k的增大在增大，但是翼型上产生的气动力由于有效迎角的变小在减少，而且振动轴后移本身会带来负相位，这就大大抵消了惯性力带来的额外升力增量，表现出来的就是k增大，相位增加缓慢。

图16 绕前缘和后缘振动时翼型周围流场随k的变化(Re=7.89×105)Fig.16 Variations of flow field around airfoil with k when pivot located at leading edge and trailing edge (Re=7.89×105)

3.3 推论及应用

从3.1节和3.2节的分析可知，利用已知的计算结果得到绕其他振动轴位置振动的升力系数曲线(幅值会略有差别)是可行的，例如，当k=0.30，Re=7.89×105时，从表1可以看出，绕x=0.50c处振动时CL-t曲线的相位偏移为4.87°，即时间上提前0.003 s，而绕x=c处振动时，相位和时间分别为-11.52°和-0.007 1 s(负号代表滞后)，根据本文的结论，在这两个振动轴位置之间必然会出现相位为0的情况，即CL-α曲线呈现直线型，而且可以根据这两个状态推算出相位为0°时对应的振动轴位置。首先，从这两个状态可以推算出x=0.50c到后缘处这一段翼型表面的平均流动速度为

Uav=(c-0.5c)/(0.003+0.007 1)=49.5cm/s

假设振动轴位置位于x0处时，相位差为0°，即时间差也为0，从3.1节的分析可以看出振动轴位置对相位的影响主要是线性的，所以有

x0-0.5c=Uav×0.003≈0.15c

即这个振动轴位置位于x=0.65c时，CL-α曲线近似呈现直线型。

图17 k=0.30，x=0.65c时的CL-α曲线(Re=7.89×105)Fig.17 CL-α curve at k=0.30, x=0.65c (Re=7.89×105)

k=0.30,x=0.65c时的CL-α曲线如图17所示，验证了推算的准确性。相应地，如果想推算已知振动轴位置的升力系数曲线，可以利用同样的方法，推算出此振动位置的CL-t曲线与α-t曲线的相位差，如当k=0.30时，已知振动轴位置x=0.75c，利用x=0.50c和x=c的结果可以推算出其时间上滞后0.002 s，即相位差应为-3.23°，则升力系数曲线为

CL-x=0.75c=CLmean+CLampsin(ωt-3.23°)

(10)

式中:CLmean和CLamp可以由表1插值得到，这里分别为0.362和0.297。

如图18所示，推算的结果和计算的结果符合良好，可以看出本文得出的结论是正确可靠的，这对于工程实际应用有较大的意义，例如可以通过计算或实验获得容易测量位置的结果，以此推算出其他位置的结果。

此外，根据本文的分析，小振幅振动的翼型并没有牵涉到涡的形成和发展，这也意味着传统的势流理论一定程度上也可以预测这种迟滞环变向的现象。

图18 k=0.30, x=0.75c时的预测曲线和计算曲线对比Fig.18 Comparison between predicted curve and calculated curve at k=0.30, x=0.75c

本文利用面元法[30]计算了相应的状态，结果如图19所示，可以看出当k<0.30时，面元法预测的结果和基于RANS方程计算的结果高度一致，但是当k=1.00时，升力系数计算结果不仅在幅值上有较大差别，而且相位预测也有差异。这主要是因为传统的势流理论只能处理附着流，而从图16中可以看出，当k增大到一定程度时，振动翼型周围流场特别是前缘处的有效迎角被改变，因此面元法计算结果也和CFD结果相差较大。但是，面元法在一定程度上还是提供了一种更加快速的研究小振幅振动翼型气动特性的方法。

图19 面元法与CFD动网格计算结果对比(Re=7.89×105)Fig.19 Comparison of calculated results of panel method and CFD sliding mesh (Re=7.89×105)

4 结 论

1) 迟滞环现象主要是升力系数、力矩系数随时间变化的曲线在相位上与迎角变化规律曲线的差异，当升力系数曲线与迎角随时间变化曲线的相位差φ>0°，即升力曲线相位提前时，升力系数随迎角变化的迟滞环曲线呈现顺时针变化规律，而当φ<0°，即升力曲线相位滞后时，迟滞环曲线呈现逆时针变化，当φ=0°时，此时的升力曲线恰好为直线型，而这个相位与振动轴位置和减缩频率k有着密切关系。

2) 振动轴的影响：本文的计算结果显示，振动轴位置后移会带来相位上的延迟，而且这种影响近似呈线性关系。相位上的延迟，使得迟滞环向顺时针变化就越困难，即相同的k下，振动轴的位置越靠后，升力系数迟滞环越可能呈现逆时针变化。

3) 减缩频率k的影响：减缩频率k对升力系数曲线的影响机制与振动轴不同，k的增大，带动周围空气振动从而带来的惯性反作用力增大，进而提高了升力，即提前了相位，但是并不改变CL-t曲线的频率。可以看出这种变化不再类似振动轴位置的线性影响。

4) 雷诺数的影响：本文研究结果表明，当雷诺数变大时，流动黏性会相对变弱，因此相位滞后比低雷诺数时较小，但是不会使得迟滞环现象消失，文献[13]在无黏情况下(可以看成雷诺数无穷大)也观察到了迟滞环现象，与本文结论类似。