《MATLAB软件应用》课程建设探索及实践应用

聂春燕

(长春大学 电子信息学院， 长春 130022)

MATLAB软件目前成为国际上流行的计算机仿真软件工具之一，已经被广泛地应用在工程设计的各个领域中，如测试控制、通信、电子、以及自动化等领域，属于一种功能强大、编程简单、易学、非常实用的编程语言，是通用的数值仿真、科学计算和可视化及动态仿真的重要工具，目前各大高校普遍开设了此课程。通过MATLAB 在理论和实践教学中的应用，用 MATLAB 语言描述抽象的理论知识，使理论知识更具体化，便于应用于实际工程中[1]。尤其对于电类课程中很多枯燥的理论内容，非常需要仿真软件去形象逼真地展示过程和结果，所以，让学生掌握一门仿真软件势在必行。教学服务于应用，使《MATLAB软件应用》课程的教学与科研、应用紧密地结合起来，突出实践应用,为他们后续专业课的学习、、课程设计、毕业设计、科研活动等打下仿真知识的基础。

1 MATLAB 软件简介

20世纪70年代，美国New Mexico大学计算机系主任Cleve Moler博士在给学生讲授线性代数时，发现学生们应用EISPACK和LINPACK库程序编写FORTRAN接口时特别困难，于是他自己亲自动手，在业余时间开发出方便学生使用的接口程序，并且用MATrix和LABoratory两个单词的前3个字母组合成一个名字叫MATLAB[2]。在这之后，MATLAB软件作为教学仿真软件在很多所高等学校中被应用，而且作为一种免费的仿真软件被广泛流传。当今，人们普遍使用的MATLAB软件是MathWorks公司用C语言开发的。该仿真软件已经被确认为可靠、准确的科学仿真标准软件之一。

2 《MATLAB软件应用》课程开设的必要性

当前许多理工科院校已经将MATLAB仿真软件列为学生必须了解的仿真软件，也是教育部指导委员会指定要求的一门仿真软件课程。长春大学电子信息学院(以下简称学院)的电子信息工程专业、通信工程专业、测控专业、物联网、电气及其自动化等专业都开了这门课程。学院从2006年开设《MATLAB软件应用》以来，通过本课程的讲授，旨在提高学生解决实际工程仿真的能力。将MATLAB 软件作为一个工具引入课堂教学中，用软件仿真方式加深学生对相关课程重要知识点的理解。一些课程由于理论推导复杂、绘图比较难，尤其数学计算过程比较繁琐复杂,经常使一些学生感到学习内容难于理解。MATLAB仿真是理论联系实际的重要纽带[3]。将MATLAB语言引进课堂进行教学，教师可以边讲解、边操作，使授课内容丰富、直观，可以有效提高课堂教学效率[4]。例如在对自动控制系统的性能分析中，以往课堂上需要在黑板上花费很多时间绘制系统响应曲线，而利用MATLAB软件可以方便地绘制出系统响应曲线并且还可以动态演示，使得教学内容一目了然，便于学生理解抽象的教学内容，提升学生理解能力。

3 课程建设措施及教学方法

我校的办学宗旨是以培养应用型和创新型人才为培养目标，作为课程组教师经常到相关院校进行学习，同时借鉴国内外优秀院校的先进教学理念以及教学改革成果。

3.1 《MATLAB软件应用》课程建设的措施

(1)不断完善课件和课程网站的建设，录制微课、慕课等，增加网络视频教学，丰富网上课程资源，为直观地展现教学内容，便于课后学生复习，学生提供一个具有独立、自由、开放、灵活、丰富的学习空间。

(2)增加网上实时答疑辅导，实时解答学生的疑问。

(3)在教学内容选择上，尽量与学生所学专业相结合；课堂上，巩固所学知识的同时，力争激发学生的学习兴趣，提高学生创新、动手的应用能力。

(4)积累教学经验，修订教材，增填实际工程中的应用实例以及涉及的后续相关课程的仿真实例。

(5)课堂上采用灵活的授课方式，融入比较式教学和启发式教学的理念，充分调动学生学习的主动性和创造性。

3.2 课程建设中的教学方法

《MATLAB软件应用》课程主要讲授二维绘图、自控原理、电路、信号与系统、数字信号处理以及通信工程等多种课程中的仿真应用实例。

(1)实时操作式教学。所有课程内容均采用多媒体教学。在机房里授课，基于仿真教学的需要，可以做到实时仿真、实时解决问题。通过大量的应用实例讲授系统建模仿真的基本方法和技巧，从而解决专业课程的学习、科学研究和实际现场工程中的仿真问题。

(2)启发式教学。该种教学方法是在课堂教学的过程中，教师提出问题，积极引导学生去思考，从而增强学生的求知欲。加强学生的联想思维、发散思维的能力及创新能力，加强课堂上的师生互动，是一种行之有效的教学方法。

(3)多种教学手段相结合式教学。采用上机和多种媒体为主的教学手段，针对不同的教学内容寻求最佳的表述方式，如实时演示、虚拟仿真、动画课件等。对于偏重操作的MATLAB软件学习，辅以实例进行演示，会令学生对知识点的掌握更加直观明了，同时也更容易激发学习的兴趣[5]。将现代教育技术充分运用到MATLAB仿真课程的教学中，可以丰富教学内容，达到在有限的学时内，为学生提供丰富的信息量。

4 MATLAB软件在专业中的应用实例

MATLAB软件可以充分将理论和实践相结合，能使学生更好地将理论应用于工程实践中。MATLAB仿真软件可以完成信号与系统的分析,能够更准确、快速和直观地得到可视化仿真结果, 教学效果生动形象。

下面给出几个MATLAB仿真实例。

实例1求LTI线性时不变系统的冲激响应和阶跃响应。已知系统输入输出微分方程如下：

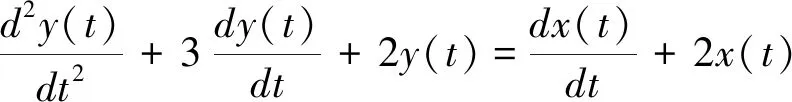
编制M文件如下：

a=[2,3,5];b=[2,1]; %赋初始值

figure(1),impulse(b,a) %画出冲激响应

grid on

figure(2),step(b,a) %画出阶跃响应

grid on

运行以上程序，得到冲激响应波形图和阶跃响应波形图，分别如图1和图2所示。

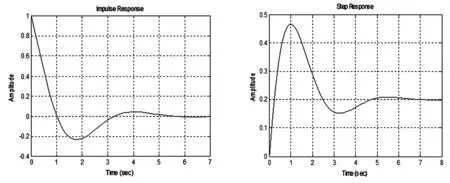
图1 系统冲激响应 图2 系统阶跃响应

综上可见， MATLAB仿真软件可以生动形象地让学生快速了解线性时不变系统的冲激响应波形和阶跃响应波形的真实具体形态。

《自动控制原理》课程所研究的自动控制规律，具有一定的抽象性。掌握其基本问题、 方法和思想对初学者来说较为困难。

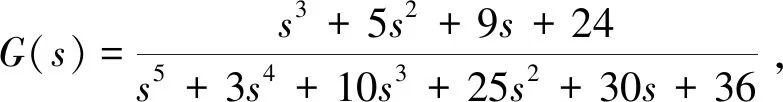
在MATLAB命令窗口输入如下：

num=[1 5 9 24];

den=[1 3 10 25 30 36];

sys=tf(num,den); %建立连续系统的连续函数

pzmap(sys)

运行程序的结果如图3所示。

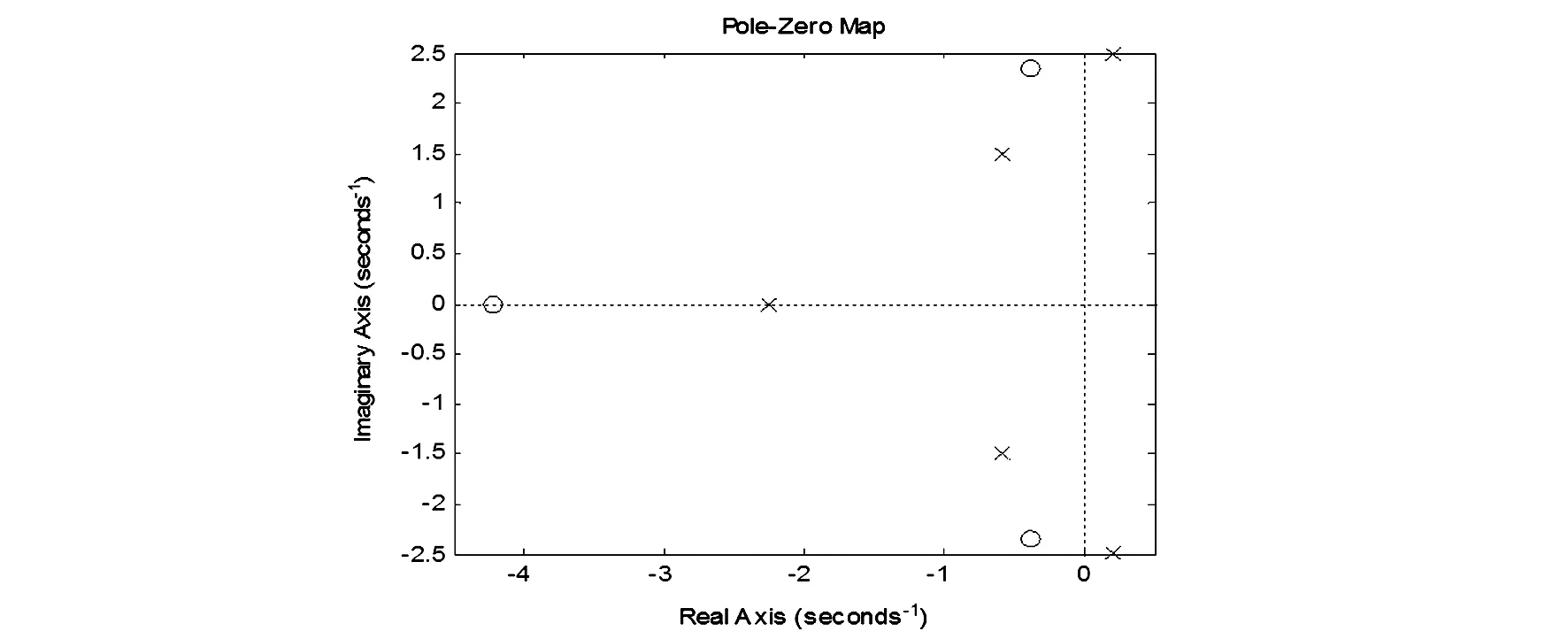
图3 系统的零极点图

由图3可知，该系统有位于s右半平面的极点，因此系统不稳定。可见，在《自动控制原理》课程的教学过程中，教师有时需要分析多个控制变量、绘制多条曲线，很难画出准确的曲线。但 MATLAB 可以很迅速地绘制出不同环节的图形，便于学生理解记忆。

曲线拟合是根据一组或多组数据找出可以描述数据走向的一条曲线的过程，是人们设法找出某条光滑曲线最佳的拟合数据，其是评价是否准确描述测量数据的常用的方法。

实例3如数据 x=[0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1]和y=[-0.32 0.75 1.86 4.56 5.14 6.43 7.21 9.2 10.78 12.66 15.86]，画出数据点，对数据x和y再做9阶多项式曲线拟合，并在同一坐标里分别绘出原数据曲线、二次拟合曲线、9阶拟合曲线。

程序如下：

x=[0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1];

y=[-0.32 0.75 1.86 4.56 5.14 6.43 7.21 9.2 10.78 12.66 15.86];

p2=polyfit(x,y,2);

p9=polyfit(x,y,9);

x1=linspace(0,1,60);

y1=polyval(p2,x1);

y2=polyval(p9,x1);

plot(x,y,'*r',x1,y1,'--',x1,y2,'b')

程序运行结果如图4所示。

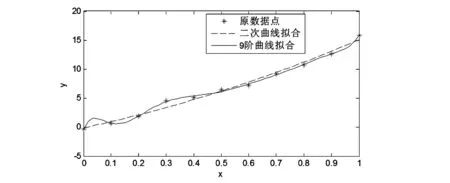
图4 原数据、二次拟合曲线与9阶拟合曲线

通过对图4分析可知，在实际工程中，为了提高拟合准确性，常采用高阶多项式进行拟合所测量的数据。但是，如果提高多项式阶次，也会给拟合曲线带来局部波浪曲线，从而增加拟合的均方误差，对工程中的数据分析带来不利影响。因此，对测试数据进行拟合分析时，一定要综合考虑拟合的阶次和均方误差的因素，才能充分让拟合发挥其作用。

6 结语

《MATLAB软件应用》课程主要讲授MATLAB仿真软件的各种功能与应用，是培养应用型和创新型人才必修课程之一。在该课程建设中，不断改革课程的教学内容、教学方法、教学手段和考核方式等。通过本课程的学习，可以提高学生解决工程实践的能力和创新能力。