机器人抛磨自由曲面的分片路径规划研究
于 淼,刘新星
(长春大学 机械与车辆工程学院,长春130022)
自由曲面的抛磨,极具复杂性和困难性。既要求效率,又要求精度。而传统的抛磨方法,一种是人工抛磨,工人根据经验,来完成加工工件的精度要求,其加工的工件随机性大,精度往往不能一致,效率不高[1-2]。另一种是半自动加工,机器通过抛磨工具,来完成对工件的抛磨。但自由曲面的形状复杂,凹凸性大,曲率变化也较大[3],导致用磨抛工具来抛磨的工件精度低。由此,为了提高抛磨自由曲面的加工效率和加工精度,作者提出基于曲率和加工工艺相结合的复杂自由曲面的二次分片规划技术。
1 自由曲面分片抛磨原理
当抛磨自由曲面时,由于自由曲面的曲率变化大,且大小不确定,从而使抛磨工具在进行抛磨时,速度发生变化,磨削力也发生变化,最终导致抛磨工件的精度降低,所以要求划分抛磨加工区域[4],使工具在加工工件时,加工区域的工件曲率变化在一定范围内,磨削力较均衡,从而使抛磨精度更高。分片抛磨就是根据自由曲面的几何性质和加工工艺,将自由曲面分成若干子曲面片,在不同的子曲面片使用不同的工具,来提高抛磨精度。
2 自由曲面分片规划
2.1 建模
对于一个自由曲面,NURBS能很好地表达其特性,故用NURBS来建模[5-8]。
被抛磨自由曲面的有理式表达式为:
(1)
式中:di,j(i=0,1,...,n;j=0,1,...,m)为控制顶点;ωi,j(i=0,1,...,n;j=0,1,...,m)为与顶点di,j对应的权因子;P(u,v)为曲面上与参变量u,v相对应的值;Ni,k(u)、Nj,l(v)分别为u向k次和v向l次的规范B样条基,它们由de Boor Cox递推公式(2)决定[9]。
(2)
2.2 自由曲面分片
2.2.1 曲率计算
曲面上法曲率的最大值和最小值称为主曲率,用kn表示,求取主曲率及其方向可用法曲率对表示方向的比值求导并使其等于零[10],方程如下:
(3)
(4)
式中:E、F、G为第1基本量;L、M、N为第2基本量。
求解方程(3)、(4)可得到曲面上的一点s(u,v)的主曲率k1、k2:
(5)
式中:高斯曲率K和平均曲率H为:
(6)
根据求得的H和K可得曲面分片的基本曲率基础。
2.2.2 依据曲率的一次曲面分片
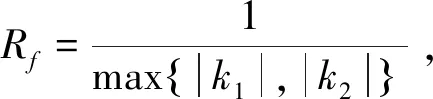
2.2.3 根据加工工艺的二次曲面分片
机器人抛磨的路径规划中,其轨迹是等间距矩形时的路径规划效率最高。根据曲率分成的子曲面片形状不规则,而机器人的最佳路径却是等间距矩形,所以在以曲率分成子曲面片的前提下,再把不规则形状的子曲面片进一步分成矩形子曲面片。以最边角的不规则形状为起始,以x轴和y轴为长和宽的基边构建矩形。把子曲面片分别投影到x轴和y轴的最大长度作为x轴和y轴方向上的边,构建矩形。相邻的两个矩形若有重合,则求差。依次投影、构建矩形、求差,直到把所有的子曲面片完成为止。从而得到基于曲率和加工工艺的二次曲面分片。
3 仿真研究
构造自由曲面,如图1所示。
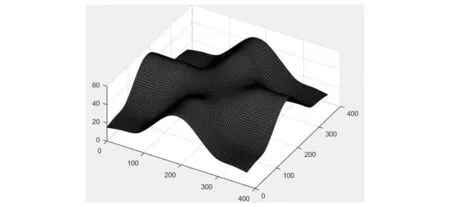
图1 自由曲面三维图
对自由曲面进行曲率计算,曲率图如图2所示。
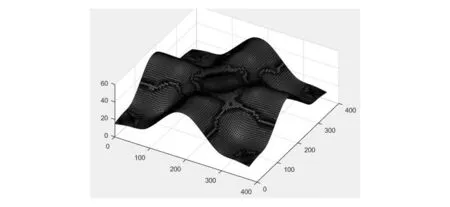
图2 自由曲面的曲率图
提取自由曲面的曲率信息,依据曲率的某一范围,划分自由曲面,如图3所示。
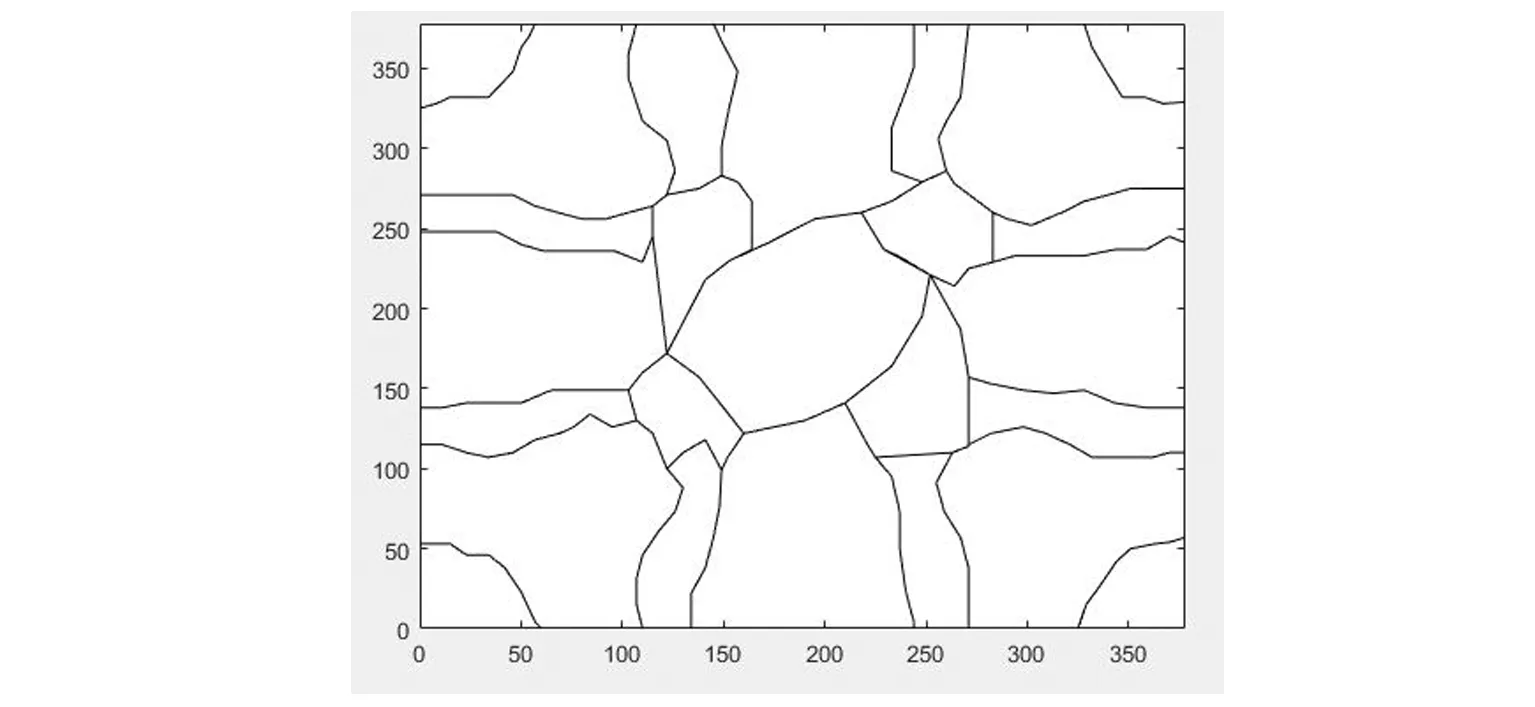
图3 按曲率范围划分的子曲面片平面图
在曲率划分的子曲面片基础上,综合加工工艺,即机器人在抛磨的过程中,受灵活运动空间、抛磨力、位姿等的约束,轨迹是等间距矩形时,抛磨的效率最高,精度最高,所以进一步划分成矩形子曲面片,如图4所示。
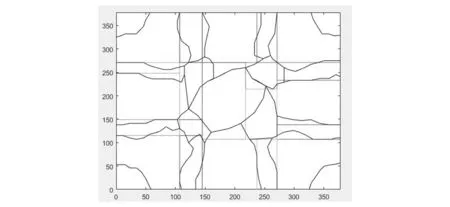
图4 二次分片图
通过计算机Matlab仿真,经过二次分片,把一块复杂的、非规则的自由曲面,分成21块曲率相近、便于机器人抛磨的矩形子曲面片,每个子曲面片的曲率在0.02mm左右,保证了机器人在抛磨时不会产生干涉。
4 结论
通过对NURBS、自由曲面的理论研究,结合机器人抛磨自由曲面的加工工艺,提出自由曲面通过曲面曲率和机器人抛磨加工工艺相结合的二次分片理论,由一个复杂的、非规则的曲面分成若干个曲率相近的矩形子曲面片,使抛磨工具和工件能最大限度的相互适应,提高抛磨加工精度。同时,在此理论的基础上,通过Matlab仿真软件,作出了计算机仿真,给出了具体的方法和确定的程序算法,为进一步的工业机器人抛磨自由曲面提供了理论基础和方法。

