概念图在初中数学复习教学中的应用*——以苏科版“第7章 平面图形的认识（二）”为例

☉江苏省运河中学 袁 健

由约瑟夫·D·诺瓦克于20世纪70年代，在康奈尔大学发展出概念图绘制技巧.当时，诺瓦克将这种技巧应用在科学教学上，作为一种增进理解的教学技术.“概念图”是一种知识及知识之间关系的网络图形化表征，也是思维可视化的表征.

现代认知心理学认为，长时记忆中的信息不能提取或提取失败的原因是失去了有助于回忆的编码线索，或者在储存时没有适当编码.使用概念图组织教学能帮助学生建构相关知识，并对知识进行编码工作，提高学生对知识进行有效提取和应用知识的能力.本文主要以苏科版“第7章 平面图形的认识（二）”为例，从全章知识、基本图形、数学思想三个方面表述概念图在初中数学复习教学中的应用.

一、构建全章知识的概念图

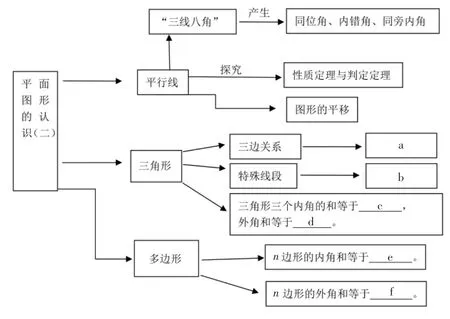
图1

将制作好的全章知识概念图（如图1），分发给每个学习小组.要求每组学生将方框内小写字母代表的内容填充.学习小组经过讨论后，由小组代表交流结果.如果有疑问，再通过小组之间的讨论及教师总结，得出最终的正确答案.（a：三角形的任意两边之和大于第三边，b：三角形的中线、角平分线、高线，c：180度，d：360度，e：（n-2）·180°，f：360°）

数学家康托尔曾经说过：“在数学的领域中，提出问题的艺术比解答问题的艺术更为重要.”上述学习过程中，学生只是对平面图形的认识（二）有一个框架性的理解.为了让学生进一步掌握与平行线相关的知识、定理，需要提出以下问题讨论：①你能识别同位角、内错角、同旁内角吗？能画出图形进一步说明它们分别是由哪两条直线被哪一条直线所截形成的吗？②平行线的性质定理有哪些？平行线的判定定理有哪些？它们是什么关系？学生通过回答这两个问题回顾同位角、内错角、同旁内角产生的前提，同时理解只有两截线平行时，同位角、内错角才相等，同旁内角才互补.理解平行线的判定定理与性质定理的互逆关系.③图形平移的定义是什么？它的基本性质是什么？利用平移的性质进行作图的步骤是什么？④三角形的三边关系式还可以理解为什么内容？引导学生通过不等式的变形感受三角形的任意两边之差小于第三边.⑤三角形的角平分线、中位、高线有哪些功能？你认为针对这三种线能出什么样的题目？从而引导学生看到角平分线的条件想到角度计算与证明角相等问题，看到中线的条件想到计算线段长度、三角形面积等问题，看到高线想到三角形的面积计算及角度计算问题.⑥三角形的内角和为180°、外角和为360°是怎样证明的？⑦多边形的内角和为（n-2）·180°、外角和为360°是怎样证明的？学生可以由合情推理到演绎推理证明三角形和多边形的内角和与外角和，进而重点引导学生回顾演绎推理的证明过程.（答案略）学生把所学的知识通过概念图“学进去”了，然后小组交流阶段又“讲出来”了，整体上把握了全章的知识模块和结构.

二、构建基本图形的概念图

史宁中教授指出，几何教学应注重原型启发.为了能让学生在形上更深刻地理解图形，笔者引导学生从本章的基本图形入手建构概念图.将制作好的卡片（图2）分发给每个学习小组.要求先标出三条线的名称，再说出∠1与∠2在每个图形中是哪两条直线被哪条直线所截形成的什么角.从识别同位角、内错角、同旁内角引出F、Z（或N）、C（或U）型基本图形及变式图形.为了一图多解，用该图还可以引出平行线的性质定理与判定定理的符号表达，小组内可以讨论交流，接着由小组代表展示交流.

类似地，从应用平行线的性质和判定引出M型等基本图形，求出一些角的关系.下发卡片，如图3第1题，请你求出∠ABC、∠BCD、∠CDE这三个角之间的等量关系式，并写出理由；如图3第2题，从学习三角形的角平分线引出两内角（一内角、一外角或两外角）角平分线相交的角与第三个角的关系的基本图形，请你求出∠A与∠BDC之间的等量关系式，并说明理由.从借助三角形内角和为180度引出“8型”基本图形，并求出相关角存在的等量关系式；等等.活动安排，均为先小组讨论，再小组代表发言，教师给予指导.

图2

几何部分有三种语言：文字语言、符号语言、图形语言.笔者鼓励学生在交流基本图形时，让学生充分感受图形及其变式图形之间的关系，结合图形语言用符号语言把一些线段、角的数量关系等表示出来，更容易形象记忆，这也符合初一学生以形象思维为主的认知规律.利用概念图形象地回顾基本图形、题型及变式图形、题型来，让学生更自信地面对解题，提升学习能力，可谓事半功倍.

三、构建数学思想的概念图

图4

在复习时，笔者引导学生在知识生成过程中感悟数学思想，让思维可视化，形成数学思想概念图.初一阶段常使用的数学思想有：数形结合思想、转化思想、类比思想、归纳思想、推理、分类讨论思想等.如本章知识十分注重合情推理、演绎推理相结合，进而体现了数学的严谨性.如图4，以推理思想为例，笔者引导学生构建平行线判定定理和性质定理的推理思想概念图（文字语言方面）.通过操作活动合情推理得到一个基本事实“同位角相等，两直线平行”，然后通过演绎推理证明得到“内错角相等，两直线平行”“同旁内角互补，两直线平行”.接着证明它们的逆定理成立.贯穿这几节课，让学生感悟平行线判定定理的生成过程，同时感受合情推理和演绎推理的密切关系.由角的数量关系说明直线的位置关系或由直线的位置关系说明角的数量关系，渗透了数形结合和转化的数学思想.数学家高斯认为，数学中一些美丽定理有这样的特性：它们极易从事实中归纳出来，但证明隐藏得极深.笔者在教学中要求能力较强的学生将上述5个定理用图形和符号语言推理证明.与先前构建的概念图不同的是，由于不同的小组、不同的学生对知识的理解、领悟能力各不相同，再加上提出了符号推理证明的要求，此处概念图的完成速度差异比较大.有些小组构建的不完整，有些小组的概念图不仅能整理出它们的内在关系，还能把每个定理的证明过程用符号推理表达出来、讲出来.因此，此处的概念图可以采用先组内合作再组间合作的学习方式.交流一段时间后，小组派代表进行班级汇报交流，教师点拨、评价.小组合作学习可以平衡不同学生之间的基础差异，培养学生的合作意识、表达能力.

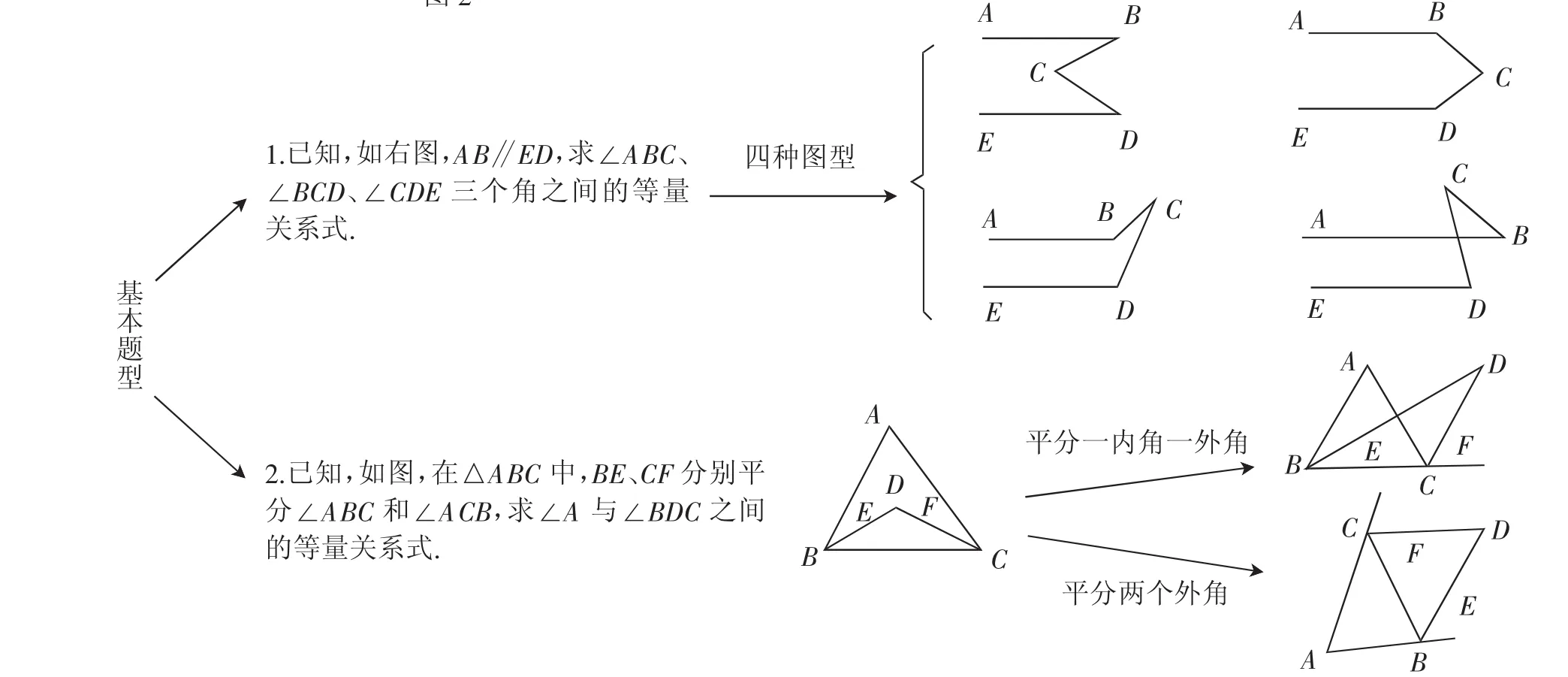
图3

在学习多边形内角和定理的推导过程时，笔者在理解教材的基础上引导学生用转化的思想将一个四边形、五边形、六边形、…、n边形分割成三角形，进而归纳出n边形的内角和公式为（n-2）·180°，在这个过程中，学生还充分感受了由特殊到一般的归纳的数学思想.通过这章内容的学习，让学生充分感受从数学思想的角度总结知识，提升学生的思维深度，进而为今后更好地学习数学打下基础.

新授课之后，一些概念在学生的头脑中是零散的、不系统的，概念之间的联系也相对贫乏，整合不够.因此在复习教学时要充分应用概念图，将知识、图形、思想、思维可视化的同时，对所学知识进行梳理、拓展、提升.在学习过程中，独立学习与小组合作学习相结合，构建、分析和修改概念图，使学生的学习主体地位得到落实，思维能力、认知能力、学习能力得到提高，启发引导学生学会学习，培养学生的核心素养.F