采用SG平滑滤波的Stewart平台主从控制研究

郭云鹏，张 弓,侯至丞,王卫军,2，王 力，韩彰秀,2

(1.广州中国科学院先进技术研究所，广东 广州 511458；2.深圳市中科德睿智能科技有限公司，广东 深圳 518055)

0 引言

机器人的离线路径规划一般适用于已知作业环境。对于未知环境的完全自主在线路径规划，需要引入各类传感器及复杂的控制算法，成本高、难度大。主从式机器人控制方式是在机器人控制中引入主手设备，以机器人作为从手，通过人操控主手间接控制机器人，是未知环境中机器人的主要路径规划方式[1]。美国的达芬奇手术系统(Da Vinci surgical system,DVSS) 外科手术机器人系统[2]、英国的Endo Assist机器人辅助内窥镜操作系统[3]、天津大学主导研制的“妙手”微创外科手术机器人系统[4]，以及美国NASA的空间站遥操作人形机器人[5]，均采用主从控制，实现手术机器人的操控。当前，主从控制研究的关键在于从手跟随主手运动的平滑度与实时性。

Stewart并联平台具有6个自由度，可以完成复杂的任务指令，广泛应用于运动模拟、装配、检测等领域[6]。SpaceMouse三维鼠标通过内置光学传感器实现6自由度的运动数据采集，便于控制工程模型和虚拟摄像机的空间位置[7]。将SpaceMouse用作Stewart平台主从控制的主手，可以在自由度上形成一一对应，从而增加操控的自然性和舒适性。为此，本文以Stewart并联机器人作为控制对象，以三维鼠标SpaceMouse作为控制主手，实现了两者之间的主从控制，并对其平滑度与实时性进行了试验研究。

1 主从映射模型

根据主手与从手的相对结构，主从操作系统可以分为主从同构型和主从异构型两种结构。主从手结构如图1所示。

图1 主从手结构示意图

主从手构型的优点是主从映射较为简单，从手末端位姿控制易于实现;缺点是受从手结构的限制，通用性差，难以达到人机工程学要求。主从异构型主手采用完全独立的设计，具有较好的通用性，且能兼具人机工程学的设计要求；缺点是控制模型更为复杂，需要实时求解主从系统的正反运动学甚至动力学[8]。本文主手为市场通用的三维鼠标SpaceMouse，从手为经典Stewart平台，属于异构型主从结构。但由于主手的通用性，其在人机交互上具有易用、可靠的特点。

1.1 主从映射方式

SpaceMouse可以实现6个自由度的运动输出，包括前后、左右方向的侧移和侧倾，上下的拉伸以及周向的扭转。Stewart平台具有前后、左右的平移，升降，俯仰，偏航以及横滚6个自由度。因此，在自由度上，主从手之间具有一一对应的关系。为符合人的自然操作习惯，对主从手间作自由度上的映射，如表1所示。

表1 主从手自由度映射

基于主从手间在运动自由度上的一一对应关系，主从运动映射既可以是空间点对点映射，也可以是增量式映射。增量式映射输入的是相对位姿，控制更为简单且误差可控，尤其适用于主手工作空间较小且灵敏度高的情况[9]。

图2 主从运动映射流程图

1.2 运动学反解

从图2可知，为实现从手Stewart跟随主手Space Mouse运动，除了建立主从手间的运动映射关系外，还需计算Stewart平台的运动学反解。

根据并联机构相关理论，建立Stewart平台坐标系[10]如图3所示。图3中，Ai(i=1,2,…,6)为上平台铰点中心，Bi(i=1,2,…,6)为下平台铰点中心。静坐标系O-XYZ与下平台固联，原点O位于下平台中心，OX轴和OY轴都在静平台平面内并且OY垂直于B3B4；动坐标系p-xyz与上平台固联，原点p位于上平台中心，px轴和py轴都在动平台平面内并且py垂直于A3A4。

假设动平台的位姿广义坐标为q=[x,y,z,α,β,γ]。其中：x、y、z为动坐标系原点p在静坐标系中的坐标；α、β、γ为动坐标系相对于静坐标系的∠RPY表示。根据∠RPY及旋转变换理论，可得相应的旋转矩阵：

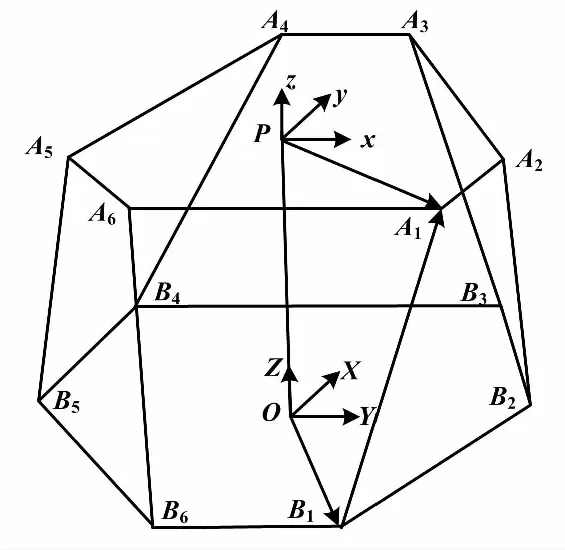
图3 Stewart平台坐标系

R=Rot(z,γ)Rot(y,β)Rot(x,α)=

(1)

由式(1)可得第i根驱动杆的长度为：

(2)

2 运动平滑性分析

通过人工操控主手时，会不可避免地产生一定的抖动。由图2可知，主手端的抖动必然会复现至从手端，从而影响从手的响应，过高频率的抖动甚至会损坏驱动电机。因此，有必要对主手端的输出进行一定的平滑处理[11]。

本文采用Savitzky-Golay(SG)滤波方法，对运动数据进行平滑处理。SG滤波是一种在时域内基于局域多项式最小二乘法拟合的滤波方法。其最大特点是在滤除噪声的同时可以确保信号的形状、宽度不变，因而被广泛运用于图像处理中[12]。

2.1 原理分析

考虑一组以n=0为中心的(2M+1)个数据x[n]，利用多项式对其拟合：

(3)

得到最小二乘拟合残差为：

(4)

根据Savitsky和Golay的发现，利用卷积运算可以求取拟合多项式的常数项，即对输入数据进行加权平均：

(5)

由微积分知识可知，若要ε最小，ε对各个参数的偏导数都应为0，即：

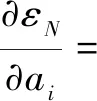
(6)

化简得到：

(7)

式中：i=0,1,…,N。

引入一个(2M+1)行、(N+1)列的辅助矩阵A，令：

A={an,i}

(8)

式中：an,i=ni,-M≤n≤M,0≤i≤N。

引入另一个辅助矩阵B，使得：

B=ATgA

(9)

经计算可得：

(10)

于是有：

Ba=ATAa=ATx

(11)

a=(ATA)-1ATx=Hx

(12)

式中：x=[x[-M] …x[M]]T；a=[a[0] …x[N]]T；H为所求卷积系数。

2.2 仿真分析

为验证SG滤波平滑效果，在Matlab中编写程序测试。给定一个长度为1 000的正弦波信号，在该信号的基础上加入服从正态分布的随机噪声，并分别选取多项式拟合的数据长度以及阶数：①长度30，阶数3；②长度30，阶数1；③长度10，阶数3。经过SG平滑处理前后的滤波效果对比可知，SG滤波在平滑数据的基础上,很好地保留了原来信号的形状和宽度。通过对比不同多项式拟合的数据长度和阶数的平滑效果(即数据个数2M+1和阶次k的不同组合)可以发现：阶数越大，越接近原信号形状，平滑效果越差；数据长度越大，平滑效果越明显，对原信号形状的保持越低。该结果符合多项式拟合的一般规律。

3 试验研究

为实现主手对从手的遥操作，本文借助以太网组建控制系统，包括Ethernet和Ethercat通信。Ethernet负责主手与控制器，即上位机与下位机之间的数据传输；Ethercat负责控制器与伺服驱动之间的数据交换。控制器采用德国Beckhoff公司的CX5120，伺服驱动为埃斯顿ProNet系列交流伺服。系统结构如图4所示。

图4 系统结构图

本文组建的试验样机以Beckhoff公司的TwinCat作为下位机程序的开发环境，以Visual Studio MFC结合3DConnexion公司提供的SDK作为上位机开发环境。所设计上位机测试界面分两部分：一部分为SpaceMouse数据显示，包括直接采集数据以及Stewart计算缸长；另一部分为Stewart数据显示，包括实际位姿和实际缸长。

由于本文采用的主从映射为增量式映射，如果不对主手的运动输出量加以限制，必然会造成从手运动超出工作空间。因此，在试验之前必须先确定Stewart平台的工作空间。Stewart平台工作空间由平台结构、电动缸行程、虎克铰转角范围等决定。以这些决定因素为判定条件，通过空间遍历的方法，结合前文提到的运动学反解，即可完成求解。本文求解Stewart平台在6个自由度上的最大运动范围如表2所示。

表2 Stewart平台最大运动范围

主从控制下的驱动缸长度变化如图5所示。

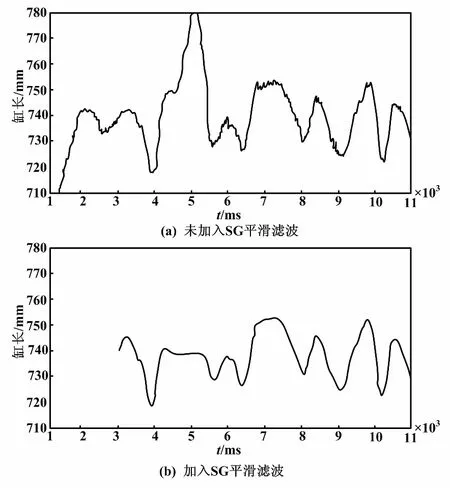
图5 主从控制下的驱动缸长度变化曲线

试验第一阶段，在不加入平滑滤波的情况下远程操控主手，获取从手Stewart平台的计算缸长与实际缸长。选取1号缸为例，从图5(a)可以看出，从手的延时大约为10 ms。但由于没有对主手进行运动平滑，导致从手的跟随运动有很明显的顿挫感。

试验第二阶段，在上位机程序中加入SG平滑滤波。其中，滤波系数设置数据长度为100，阶数为3。操控主手获取Stewart平台计算缸长与实际缸长。仍然以1号缸为例，如图5(b)所示。从手的跟随运动相较于未加滤波时更为平滑，但相应的延时增加到接近40 ms。由此可见，SG具有显著的平滑效果，但同时也增加了滞后。

4 结束语

针对机器人在特殊环境下的特殊作业要求，本文以经典6自由度并联机器人Stewart平台作为研究对象，建立以通用三维鼠标为主手的主从控制系统。分析了主从间的映射模型以及运动平滑，搭建了试验平台。试验表明，本文建立的主从控制，实现了从手跟随主手的平滑运动。由于使用了数字滤波器，从手具有40 ms左右的延时，符合一般机器人作业的实时性要求。