基于提取振源方向的频谱类型识别

顾煜炯，杨 楠，孙树民，刘 璐，徐教辉

(1.华北电力大学能源动力与机械工程学院，北京 102206；2.华北电力大学控制与计算机工程学院，北京 102206)

0 引言

汽轮发电机组振动故障诊断中，振动信号的频谱分析与识别，关系到今后诊断工作的方向。现有文献中，对频谱类型的识别方法主要有模糊识别、规则式判别、神经网络、支持向量机(support vector machine SVM)等[1-5]。实际应用中往往直接根据经验选取频谱中的特殊谱线，作为某些故障的特征频率。在故障诊断研究中，也常采用频谱中工频、倍频和分数倍频所对应的幅值比例特征，或频谱的某些统计特征(如谱的重心、各段频谱的能量比例等)作为特征向量，然后通过SVM等分类器实现识别。

由于快速傅里叶变换(fast Fourier transformation，FFT)分析存在受动态过程影响的问题，近年来出现了基于小波分析的振动信号分析方法。虽然小波分析对动态振动信号的分解效果优于FFT，但小波基不易选取，且没有从根本上解决故障激振源信息在各频段中混叠的问题。如文献[4]对碰磨和不对中故障的振动信号进行了3层小波包分解，并计算其8个频带上的区分度。计算结果显示，由于振源信息在各频带都有影响，无法确定最有效分类频带。由此可见，小波分析并不能有效分离振源信息。

基于前人在频谱识别上的研究，以及汽轮发电机组振动频谱类型识别的特点，本文提出一种基于提取振源方向的频谱类型识别方法——独立元空间重构(independent component space reconstruction，ICSR)方法。通过核独立元分析(kernel independent component analysis，KICA)方法，从高维频谱数据中提取各类典型振动故障状态激励源方向特征，并借鉴故障重构思想，从而识别故障下振动频谱所属故障类型。

1 频谱中的方向概念

从信息角度来说，高分辨率的FFT结果，可以近似恢复原始振动波形。因此，直接使用频谱的整体数据进行识别无疑是较为可信和有效的。但是，由于轴系在高速运动过程中，除本身不平衡和故障激振力产生的振动信号存在混叠外，还存在传感器误差、信号干扰等噪声，因此振动频谱类型的判别一般不易直接观察到。随着频谱分辨率的提高，在传感器采样频率随之升高的同时，频谱中的谱线数量也在增多，往往高达512、1 024甚至更多。现有研究中，大多采用定义综合信息量(重心、能量比)或从频谱中抽取部分重点关注的谱段，作为征兆信息来源；也有研究采用主成分分析(principal components analysis，PCA)法对频谱数据进行压缩，提取低维空间频谱投影点作为SVM分类器输入[2]。PCA法存在高斯分布、线性相关的假设条件限制。而由于准周期振动故障以及复杂的振动传递关系，使振动频谱数据具有非高斯分布、非线性相系的特点。因此，PCA法并不十分适合频谱信息的提取。

对汽轮机转子故障频谱特征的识别，主要分为案例总结和机理模型分析两种。在案例总结方面，刘凯等通过对振动频谱的经验总结[6]，给出了故障频谱能量分布与类别对照，如表1所示。表1中，f为机组工频。如果将各频段看作一个7维空间，以故障在各频段的比例作为坐标，不同故障即可表示为指向不同方向的向量。

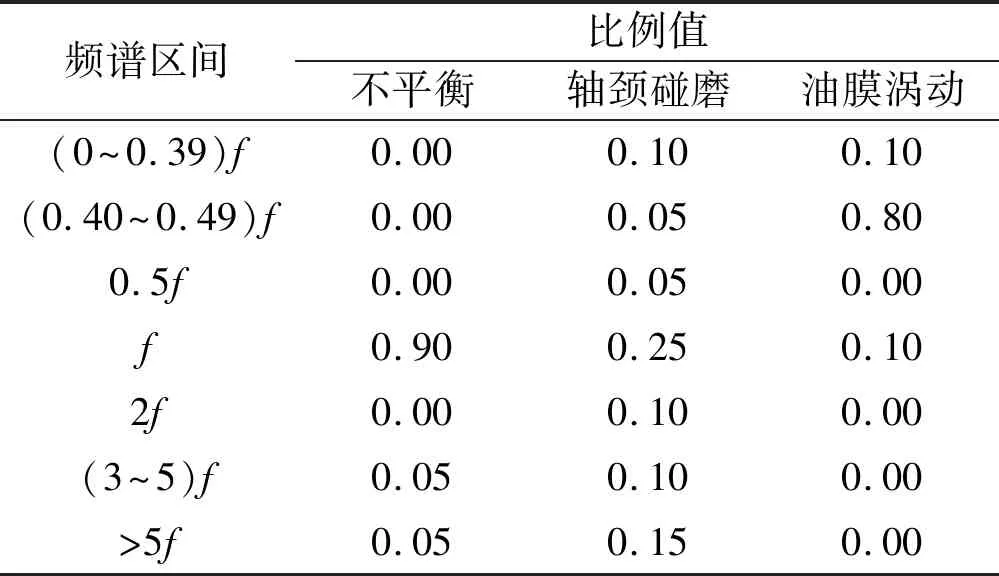
表1 故障频谱能量分布与类别对照表

从机理模型角度，对汽轮机转子振动故障产生多阶振动频率的原因进行分析时，多采用Jeffcott转子模型，获得无量纲系统振动方程[7]。

(1)

式中：Fx为水平方向非线性激振力；Fy为垂直方向的非线性激振力。

将不同故障激振力函数代入方程，通过泰勒级数展开，即可推导出碰磨、油膜涡动、裂纹等故障下的频谱类型。故障机理分析表明，不同故障在振动频谱上的方向差异，来源于非线性激振力在非线性系统中的泰勒级数展开。

实际现象和机理分析结果表明，由于非线性作用力的存在，不同故障会在频谱中表现出不同的分频谐波分量。但表1所示的各故障频谱方向存在一定相似性，且实际中的频谱也没有如此准确的比例以供对照。因此，如果能通过非线性映射，将频谱数据映射到高维空间，再以盲源分析方法提取激振源信息，理论上可以获得更加准确的故障特征信息。

2 独立元空间重构方法

机械振动故障频谱类型的识别，旨在识别振动能量在不同频率中分布的规律，并从中发现故障与频谱能量分布间的深层规律。这种故障后频谱分布的规律，本质是振动激励源成分的不同。因此，如果能通过盲源分析方法，从频谱数据中获得不同故障机理源成分，则可有效区分不同振动故障的频谱。

独立元分析方法作为一种盲源分离技术，已成为信号处理领域的热点[8]。其主要特点是根据数据的非高斯特性，使得独立元之间尽可能独立统计。与基于信号二阶统计特性的PCA方法相比，独立元分析方法不仅可去除数据间的相关性，而且能使数据间满足独立关系，因而获得更多的故障信息。

故障重构的思想是：根据不同类型故障的特征，构造去除相应故障信息的被检测数据，以判断是否可将被检测数据恢复正常，进而识别被检测数据的故障类型。以往的识别过程往往以距离作为识别标准，导致某些权重较大的特征对识别结果影响较大。而重构思想将故障的方向性和幅值分开考虑。因此，其在故障识别和故障严重程度估计领域受到了人们的重视[9]。

ICSR的基本思路如下。首先，用核函数把非线性的频谱数据映射到高维空间变为线性关系，再在核函数空间中，通过独立成分分析构建独立子空间。接着，将不同故障类型的故障频谱样本，投影到该独立子空间，获得变异最大的子空间方向作为故障特征方向。最后，在频谱识别阶段，通过新样本在不同故障特征方向上的重构效果，识别故障频谱类型。激振力方向的演变与提取如图1 所示。

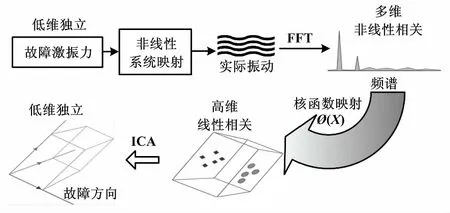
图1 激振力方向的演变与提取示意图

2.1 KICA独立空间映射

KICA是在核主元分析(kernel principal components analysis，KPCA)[10]基础上形成的、以最大化信息独立性为目标的信号提取方法。目前，KICA已在人脸识别、信号分析等多个方面得到了应用。基于KICA，将原始频谱数据映射到独立元空间(independent component space，ICS)的过程如下。

①数据映射到高维特征空间x→Φ(x)，计算核矩阵K。

②核矩阵中心化K=K-INK-KIN+INKIN。

③经协方差分解，获得白化矩阵ZTZ=I。

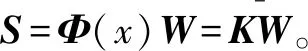
⑤计算监测统计量T2=sTΔ-1s,Δ=diag(λ1,λ2,…,λq)。λi为正常样本第i个独立元的方差，统计量T2的上限通过核密度估计得到。

核矩阵K是通过核函数映射得到的。其原理是通过一个非线性映射Φ(x)，将M维向量空间中的数据映射到高维特征空间F中，达到非线性数据在高维空间中的线性可分的目的。使用核函数方法的一个优点是在高维特征空间中进行线性学习时，不需要知道非线性变换Φ(x)的具体形式。只要满足Mercer条件的核函数替代线性算法中的内积，即K(x,xj)=Φ(xi)TΦ(xj)，就能得到原输入空间中对应的非线性算法[11]。满足条件的核函数有多种，本文选用常用的高斯核函数：

(2)

式中：c为常数，根据具体样本数据的多组交叉试验，对c进行赋值。

2.2 独立元空间故障特征方向提取

Qin等[12]首次在基于数据驱动的故障诊断领域提出了基于重构的故障诊断方法，定义了故障特征方向的概念。对于频谱类型识别来说，基于重构的频谱类型判别，将激振力幅值与方向分离，可以达到更好的识别效果。

基于重构的故障诊断思路，简单来说就是在监测空间中的不同故障特征方向上，消除监测数据中的故障部分，并以监测统计量的变化判断重构效果。如果统计量恢复正常，则说明特征方向选择正确，进而确定故障类型。假设故障方向为D，根据故障数据X∈R1×M中的正常部分x*∈R1×M，就可以通过将故障数据x沿故障方向重构，得到正常部分x*：

x*=x-fD

式中：D为一个正交矩阵，维数为lf×M，此正交矩阵表示故障所影响的空间方向；lf为故障影响空间的维数；f为在此故障方向上重构的幅度，即故障的幅度，一般随故障严重程度的不同而不同。

以PCA应用故障重构方法为例，假设主元投影矩阵为P∈RM×d，d为主元维数。通过得到正常部分x*的最佳估计(主元空间监测统计量T2最小为标准)，求不同故障方向上的故障幅度f：

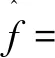
(3)

令:

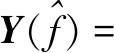
(4)

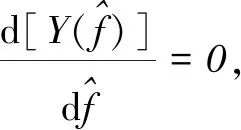
(5)

式中：D=DPPT为故障方向在主元空间中的投影。

故障重构过程可以理解为对故障数据按照不同故障方向进行分类的过程。如果新故障数据和已知故障方向匹配，则经故障重构后，故障检测统计量可回到正常阈值以下。

关于故障特征方向的定义，大致分为两种方式。一种是单一传感器或多个传感器故障，故障方向表现为相应传感器变量为1、其他变量为0的向量。例如传感器数量为5个，故障发生在第3个传感器上，则故障方向D=[0,0,1,0,0]。另一种是根据历史故障数据训练，得到故障样本的特征方向[12]。由于故障频谱维度达上百个，且其各谱线间存在着非线性耦合关系，不易直接求取故障特征方向。因此，本文选用后一种特征方向定义，采用试验故障数据，训练获得各类故障频谱特征方向。首先，通过故障与正常样本频谱训练，获得故障相关独立元方向；然后，在ICS中应用重构方法，识别故障频谱类型。

假设正常频谱的训练数据为X∈RN×M，N为训练样本数，M为频率维数。故障的频谱样本为Xf∈RN×M。首先，采用正常频谱样本训练解混矩阵W，并得到正常数据的独立元Sn：

(6)

故障频谱样本Xf通过解混矩阵W，投影到相应的ICS中：

(7)

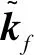
故障频谱映射到ICS后，已最大程度地消除了振源信息的关联性。当故障发生时，在ICS中表现为某方向的独立元变异。这种变异表现在幅值和方向两个方面。

首先，量化故障在ICS中的幅值变化。对故障样本独立元协方差矩阵进行奇异值分解(singular value decomposition,SVD)分解，得到：

(8)

式中：Rf∈RN×q和Lf∈Rq×q为故障样本在正常ICS中的得分矩阵和方向矩阵。

然后，在ICS中将故障独立元投影到正常独立元坐标空间，定义故障相关矩阵：

对该故障相关矩阵进行SVD分解，得到故障相关负载方向Lr∈Rq×q。故障样本独立元在Lr上的投影，反映了故障与正常独立元在ICS各方向的相对变异大小：

Rr=SfLr

(9)

根据ICS中相对方差变化衡量故障对各独立元方向的影响程度，定义故障样本得分矩阵Rf和故障相关得分矩阵Rr的相对变化率：

(10)

故障影响率TRi反映了故障对第i个独立元的相对变异程度。如果TRi大于1，则说明故障在该方向上的相对变异较大。TRi(i=1,2,…,q)中大于1的相应独立元方向，则可以得到故障相关独立元方向，即故障重构方向D:

D={TRi>1|Lf}i=1,2,...,q

(11)

故障频谱样本特征方向的提取步骤如下。

①已知故障频谱样本，用正常数据的均值和方差中心化和标准化。

②将故障数据Xf∈RN×M映射到高维空间，得到故障数据核矩阵Kf∈RN×N。其中，kf,ij=k(xf,i,xj),xj为正常数据。

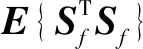
⑧计算故障相关比例TRi，并与α进行比较，得到相应故障相关独立元方向D={TRi>1|Lf}。

2.3 在线重构识别

频谱类型识别模型的训练与在线辨识流程如图2所示。

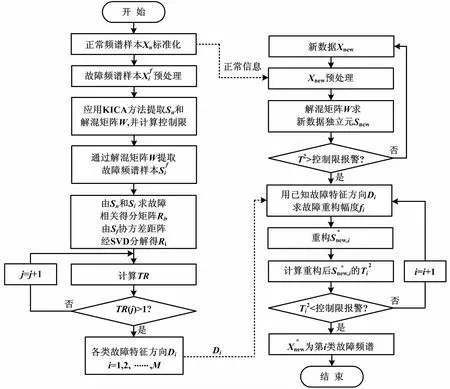
图2 频谱类型识别模型的训练与在线辨识流程图

根据KICA故障监测统计量T2定义，故障实时频谱监测统计量为：

(12)

T2统计量的控制限，由正常样本数据的核密度估计获得。

由2.2节对故障幅值的计算公式，在故障方向Di上的故障重构幅值为：

(13)

沿故障方向Di重构后的独立元为：

(14)

3 试验数据

将本文方法应用于自主研发的汽轮机振动监测与分析系统(VTDAS11)中。为了适应转子由盘车到稳定转速(3 000 r/min)期间随转速变化的整周期采样，采用同步整周期采样方式对振动数据进行采样。选用DAQ2205 A/D板作为数据采集板。该板为一款基于32位外设部件互连标准总线(peripheral conponeut interconnection,PCI)总线的高性能、功能强大的采集板。

该板最大的特点是具有成组触发采样功能，能很好地实现振动的同步整周期方式采样。将键相脉冲信号引入DAQ2205 A/D板下方的SCSIV68接口的外部触发端子，当键相脉冲信号到来时，通过软件计数，能计算出当前转速。通过倍频器产生N倍频(系统采用32倍)脉冲触发A/D转换。此时，A/D不是转换一次，而是按设定转换频率将所设定的所有采集通道自动轮询一遍，并等待下一个外部触发脉冲的到来。采样长度为1 024，即第一个键相信号触发后生成N倍频采样频率，采集振动信号1 024个点后，生成第一批采样信号，并等待下一键相信号。因此，每次振动采集经FFT分析后，可得到具有512条谱线的频谱。

3.1 试验台测试

采用BENTLY-RK4转子试验台，测试转子不平衡、碰摩、油膜涡动以及正常状态下的振动频谱。通过VTDAS11，采集振动传感器数据并形成故障频谱样本。正常和故障状态下的转子频谱如图3所示。

图3 正常和故障状态下的转子频谱

由图3可以看出，故障期间，振动频谱在不同谱线上的能量分布具有较明显的特征，即具有一定的方向性。但是具体频率上幅值的比例却与文献[6]中所提比例不完全相符。

采用本文方法对3种故障试验频谱的T2统计量进行监测，并根据3种故障样本的特征方向，对故障期间的频谱数据进行重构识别。频谱监测与重构识别结果如图4所示。

基于文献[6]的频带划分和比例计算规则，形成各故障频谱的特征向量，采用欧式距离的倒数对各类频谱特征向量间的相似性进行计算(数值越大表示两频谱越相似)。

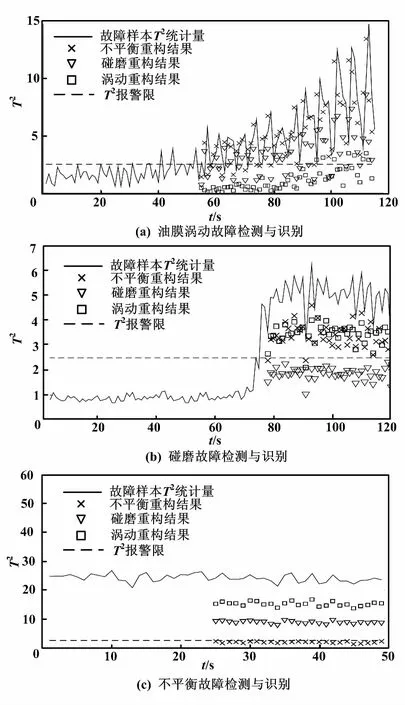
图4 频谱监测与重构识别结果

对3种故障数据与样本频谱进行交叉试验，基于欧式距离的频谱识别结果如表2所示。

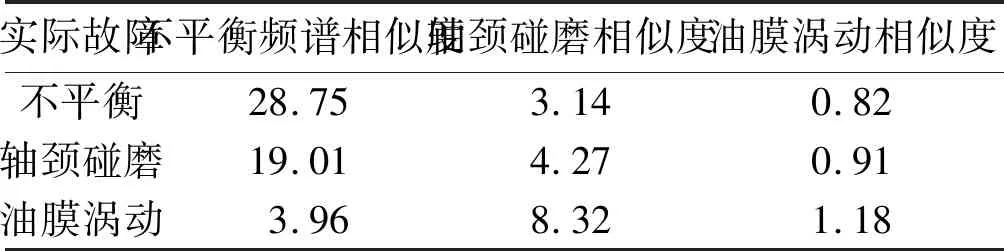
表2 基于欧式距离的频谱识别结果

由表2可知，除不平衡故障相似度判断正确外，其他两种故障都得到了错误的相似度结果，可见欧氏距离对频谱的整体识别效果并不理想。

对两种方法的确诊率和误诊率进行计算，得到频谱独立元特征方向的识别结果如表3所示。

由图4和表3可知，ICSR法不仅可以准确地判断频谱异常的发生，并且可以获得高确诊率和低误诊率的识别结果，优于直接采用欧式距离的相似度识别方法。

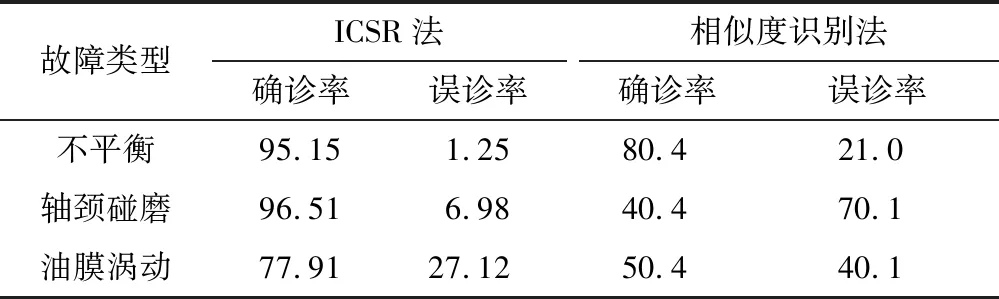
表3 频谱独立元特征方向识别结果

3.2 案例测试

某新建2×350 MW纯凝机组，采用超临界间接空冷凝汽式汽轮发电机组，锅炉为超临界循环流化床直流炉。该机组调试期间冷态启机，当过高压转子临界转速为1 552 r/min时，汽轮机诊断管理(turbine diagnosis manegement,TDM)系统检测到1#轴承的Y方向振动达到94 μm，超过报警值。在2 800 r/min时定速约40 min，期间1Y振动随转速明显增大。

此次故障发生有以下两条征兆：①在2 800 r/min定转速期间，1Y轴振呈增大趋势；②升转速到临界转速期间，1X幅值增长过快，并伴有倍频成分增加。

从频谱上看，基频和倍频有随转速升高而异常增大的现象。但振动异常初期，频谱中基频成分明显，倍频存在变化但不明显，无法判断振动的起因是转子质量不平衡，还是动静间隙变化导致的碰磨故障。

应用本文提出的方法，对启机时1#轴承的Y方向振动频谱进行分析，对早期异常频谱数据采用碰磨和不平衡两种故障模型进行重构识别。1Y轴振报警期间频谱识别结果如图5所示。

图5 1Y轴振报警期间频谱识别结果

重构识别结果显示，早期异常阶段碰磨故障和不平衡故障的重构率分别为100%和12%。因此，判断此次振动报警的起因是发生了碰磨故障。诊断建议停机后调整动静结构间隙，以消除碰磨故障措施。经后期调研，该机组后期采取调整轴封间隙的措施，使机组振动恢复正常。

4 结束语

本文基于汽轮发电机组振动故障发生时，激振力在非线性系统中传播的原理，提出一种基于提取振源方向的频谱识别方法。采用KICA方法，将频谱数据映射到独立元空间中，获得低维、独立的激励源。在独立元空间中，提取故障特征方向。借鉴故障重构的思想，识别频谱类型。试验对比和真实案例测试结果表明，本文提出的频谱识别方法，相比直接应用频谱数据进行相似性分类，有更高的准确率和更低的误诊率。