基于滑模控制器的双臂机器人控制仿真
敖天翔,李铭浩,刘满禄,2,王 姮
(1.西南科技大学信息工程学院,四川 绵阳 621010;2.中国科学技术大学信息科学技术学院,安徽 合肥 230026)
0 引言
机器人学是当今重要的研究热点之一[1-2]。目前,机械臂已在多个领域得到了广泛的应用。由于机器人系统是典型的非线性系统,近年来,滑模变结构控制理论被广泛应用于机器人控制系统中,以解决运动中存在的多种不可预见的外部干扰。Slotine[3]等将滑模控制理论应用于2自由度机械臂的控制系统中。Z.H.Man[4]应用终端滑模控制器,对多自由度机械臂进行了位置跟踪控制。A.Ficola[5]等设计了2个滑模面,实现了弹性关节机械臂的控制。刘金琨[6]针对滑模控制理论进行相关研究,其中包括了滑模理论在机械臂控制中的应用。宋崇生[7]等结合干扰观测器,利用滑模控制器对柔性关节机械臂进行了应用。万凯歌[8]等利用滑模控制器,在3自由度机械臂轨迹跟踪中取得了良好的控制效果。冯春成[9]等采用滑模控制器,在机械臂力矩估计算法的应用中取得了良好的效果。
本文在VERP机器人仿真环境中搭建机器人模型,在Simulink中建立控制系统,搭建VERP-Simulink联合仿真环境,使仿真性能与效果更加直观、可靠;通过建立机器人的运动学、动力学模型,对比了传统的逆动力学与滑模控制器的控制效果,并对滑模控制器在定点控制与轨迹跟踪控制中的效果进行了对比分析。
1 机器人模型与控制器设计
MOTOMAN-SDA20D是由日本安川公司(Yasukawa)研发的双臂工业机器人,主要应用于工业中的装配、搬运、包装等作业。该款机器人具有7轴双臂与腰部旋转轴。其中,机器人的两个机械臂可以抓取20 kg的物体,位置精度达到0.1 mm,具有很高的灵活性、精确性和协调性。以该机器人为模型搭建相应的仿真环境,并建立机器人的运动学、动力学模型,以及相应的控制系统。MOTOMAN-SDA20D机器人的左、右臂DH参数如表1所示。
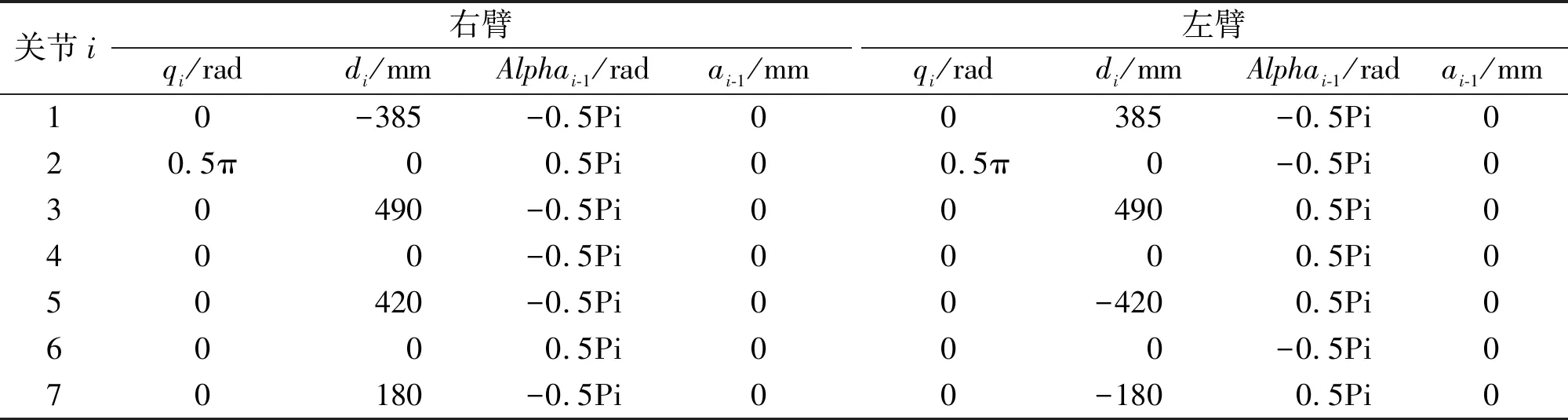
表1 左、右臂DH参数表
机械臂关节空间动力学方程(忽略摩擦力和环境接触力)[10-11]为:
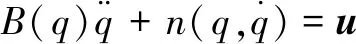
(1)
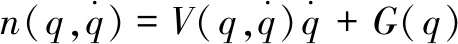
(2)
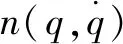
将u表示为机械臂动力学方程的形式:
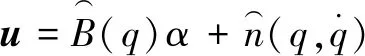
(3)
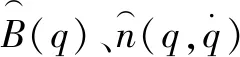
控制律α常常被设置为:
(4)
式中:KP、KD为参数矩阵。
将KP、KD设置为对角阵:
(5)
KD=diag{2ζ1ωn12,2ζ2ω2}
(6)
参考因素ri只影响关节变量qi,系统本身是解耦的,二者是由自然振荡频率ωn和阻尼比ζi决定的二阶输入输出关系。
假设位置跟踪参考轨迹为qd(t),令:
(7)
令跟踪误差e=qd-q,得误差二阶微分方程:
(8)
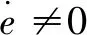
基于逆动力学的机械臂控制方法是集中控制法的代表。如果机械臂的装配误差、动力学参数取值误差较大,当忽略摩擦力、控制周期过长,将导致机械臂系统不稳定。控制系统的稳定性和快速性,非常依赖机械臂动力学模型的精确性与较高的控制系统性能。
滑模控制通过人为设计的滑动模态面,将系统状态限制在该滑模面作上、下运动。
设计误差空间的滑模面为:
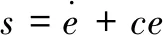
(9)
式中:c=diag(c1,c2,c3,c4,c5,c6,c7);ci(i=1,2,…,7)为正实数;e=qid-qi。
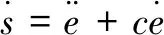
(10)
结合机械臂动力学方程:
(11)
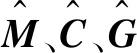
闭环系统方程为:
(12)
在设计控制系统时设计李雅普洛夫函数:
(13)
对式(13)等式两边作时间求导,有:
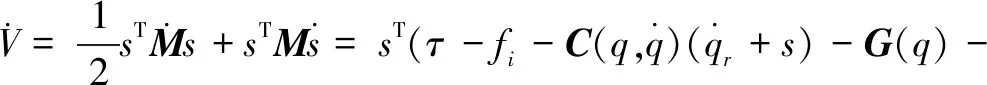
(14)
因此,滑模控制器的控制率可以定义为:
(15)
2 仿真环境搭建
仿真试验采用VERP与Matlab联合仿真的形式实现。其中:VERP是一种常用的机器人仿真软件,具有跨平台、多函数接口、集成4个物理引擎、支持7种编程语言以及良好用户界面的优点,被称为机器人仿真器中的“瑞士军刀”。而Matlab中的Simulink模块常被用于搭建控制系统仿真。
搭建仿真环境需要首先找到安川双臂机器人的3D图,依次将各个连杆的3D模型导入VERP的场景中,然后拖动各个机械臂连杆的模型,将各个连杆摆放到机械臂的初始位型。
同时,为了减少仿真中的计算量,在原位置对所有模型进行复制,并消除所复制新模型的细节描述,进行凸包化或者模型简化。将简化模型设置为可碰撞和具有动力学特性的仿真物体,用于在仿真中计算动力学特性。
将原模型设为无碰撞和动力学特性的物体,用于在仿真试验显示机器人的运动状态,并放置在简化模型支链下。在每2个连杆之间设置旋转关节,构造模型的运动链关系。
双臂机器人系统的每个机械臂都可以看作一个单独的机械臂控制系统。在Simulink中使用其对应的数学模型搭建两个相仿的控制系统,并分别设置机器人期望的角度位置、速度、加速度(或相应的运动轨迹)。通过双臂各自的控制系统,计算机械臂所需的关节力矩,并将控制信号传入VERP的系统接口中。内存共享插件负责实现Sda20控制系统与仿真环境的通信,保障VERP与Simulink之间的数据交换。系统在将力矩信号导入VERP系统的同时,也将Motoman-sda20D机器人的左、右臂的关节角度信息和关节角速度信息传送回Simulink中。
利用内存共享插件和控制周期调节插件,搭建VERP与Simulink中的机器人接口。在机器人上添加线程脚本(VERP的控制脚本使用Lua语言编写),在脚本中使用内存共享插件。在控制脚本中,将机器人关节数据(关节角位置信息,关节角速度信息)写入相应的内存共享插件。插件将控制信号从相应共享单元中的数据读出来,利用函数接口控制相应的关节力矩。因为仿真环境中的物理模型最小周期为10 ms,故设置线程的切换时间为10 ms。在Simulink中,利用Real-time Pacer插件,将仿真时间和现实时间同步。
在实际生活和仿真搭建中经常出现装配误差、测量误差和加工误差,导致机器人控制不稳定。由于仿真环境中作了大量的简化而且控制频率只能达到100 Hz,加重了控制系统的不稳定性。利用滑模控制器补偿系统建模误差,可以很好地提高系统的稳定性,达到消除机械臂角度静差、提高系统稳定性的作用。在接下来的仿真中,将对比2种控制方法在定点运动和轨迹跟踪中的效果。
3 试验仿真与结果分析
3.1 逆运动学控制
由图1可知,右臂不能稳定,而左臂最终可以稳定,系统具有很大的位置误差。因此,在仿真中,逆动力学控制算法若要得到较好的控制效果,需要精确的运动学、动力学模型。但是在实际生活和仿真搭建中,经常出现各种问题,直接导致控制不稳定(如装配误差、测量误差、加工误差和控制周期问题等)。
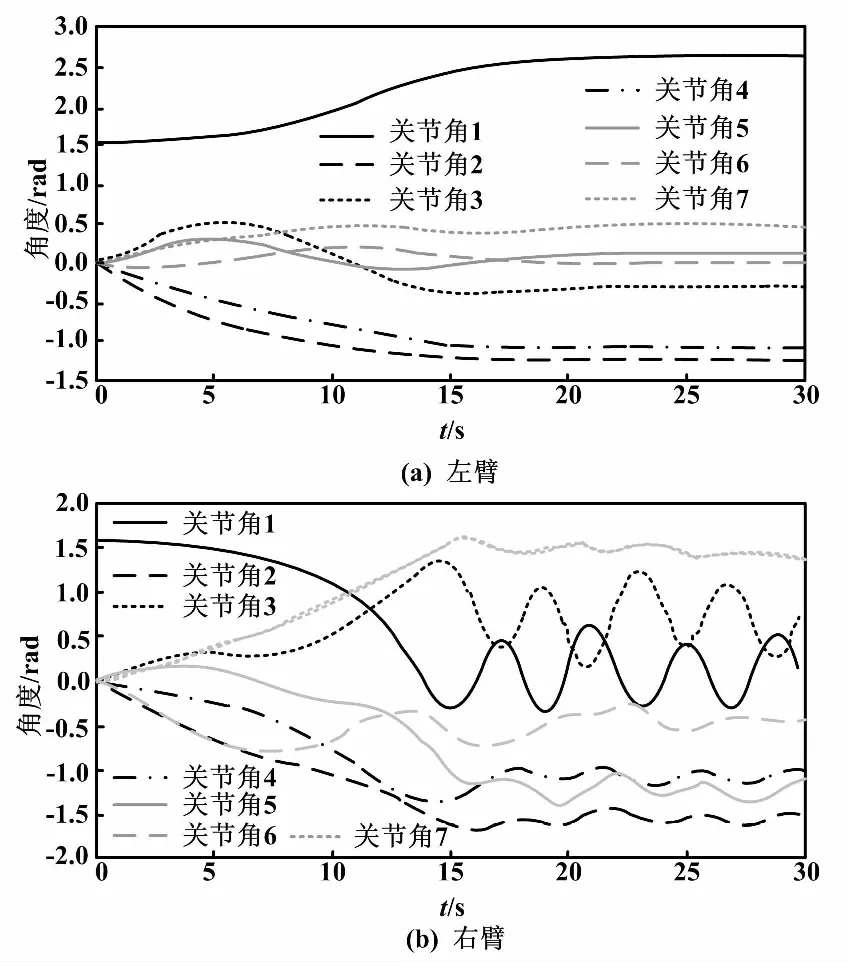
图1 左、右臂角度变化曲线(逆运动学控制)
3.2 逆运动学滑模控制
滑模控制下,左、右臂角度变化如图2所示。
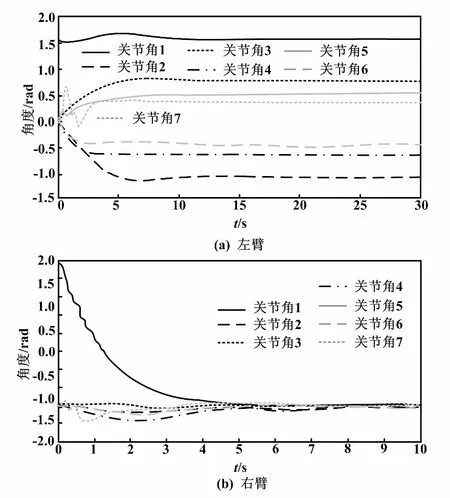
图2 左、右臂角度变化曲线(滑模控制)
滑模控制下,左臂角度误差变化曲线如图3所示。
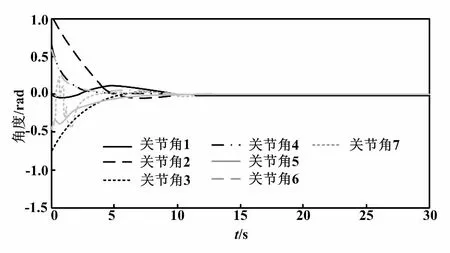
图3 左臂角度误差变化曲线(滑模控制)
由图2和图3可以看到,左、右臂都可以在10 s内到达目标位置角度,精度在0.02弧度(1°)以内。对比之前的仿真试验可知,滑模控制算法可以大大增加系统的稳定性和收敛速度。
滑模控制下轨迹跟踪的左、右臂角度变化如图4所示。
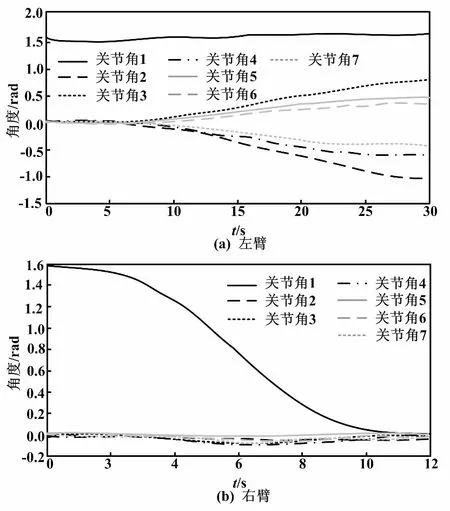
图4 轨迹跟踪的左、右臂角度变化曲线(滑模控制)
滑模控制下轨迹跟踪的左、右臂角度误差变化如图5所示。
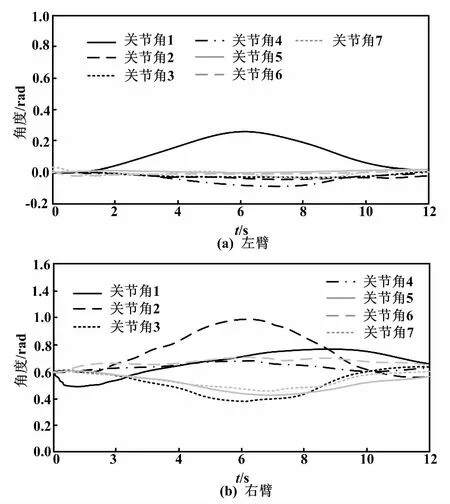
图5 轨迹跟踪的左、右臂角度误差变化图(滑模控制)
由图5可以看出,左右臂的轨迹跟踪误差在0.3 rad以内。因此,具有轨迹规划的机械臂角度变化比无轨迹规划下的机械臂更加顺滑,且不存在失控的问题,运动过程中不会出现关节角的不规则变化。
4 结束语
基于滑模控制理论,以安川Motoman-sda20D机器人为例,建立了运动学、动力学模型,以及滑模控制器。搭建VERP-Simulink联合仿真平台,设计相应的滑模控制算法,对比验证了逆动力学控制与滑模控制器的控制效果。该算法在低控制周期与模型不确定的情况下具有更强的鲁棒性。对滑模控制器的定点控制与轨迹跟踪控制效果的分析结果表明,机械臂均能快速地达到目标点,轨迹跟踪误差在0.3 rad以内。因此,利用最新的VERP机器人仿真平台,得到了更加可靠与直观的效果。

