立体几何板块第二轮复习备考建议
广东省梅州市丰顺县丰顺中学(514300) 巫纯媚
广东省华南师范大学数学科学学院(510631) 李静依
一、2016-2018年全国I卷立体几何试题考点分析
为了更好地探索命题规律,笔者将近3年全国卷I中立体几何考点整理如下:

表一 理科全国卷I立体几何考点统计表

表二 文科全国卷I立体几何考点统计表
由表一、二可知近3年全国I卷中立体几何的考查特点:
1.题量、难度保持稳定
题量一般是两小一大,分值22分(2018年文科I卷是三小一大,分值27分).其中一小题常位于5-7题中等难度的位置,另一小题为压轴题.大题位于解答题第二题,难易适中,分步设问,层次分明.
2.考点题型稳定
小题主要考查三视图、几何体的面积体积等.大题第一问较多考查简单的推理证明,侧重垂直的证明;第二问考查综合推理计算,理科主要考查线面角、二面角,文科主要考查点到面的距离、几何体的侧面积和体积.
3.注重能力考查
立体几何部分注重空间想象、逻辑推理、分析论证、运算求解等能力的考查,符合《新课程标准》要求.解答题解法多种,趋向于多想少算,其中理科第(2)问,以往以空间向量为主,近几年更倾向几何法和向量法平衡,且向量的建系难度有所降低.
二、常见考题类型
笔者通过整理近3年全国文理卷中立体几何考点分布情况,总结出如下七种常考题型:
题型一三视图

表三 三视图考查统计表
三视图是近几年高考立体几何中的重点内容,主要以小题形式出现,多是文理同题(2017年理7单独考查).主要考查方式有:由三视图求原几何体的表面积、体积、最值;根据空间几何体确定其三视图,或根据三视图的其中两个确定另一个.(目前新高考中取消三视图的内容)
例1 (2017年高考全国II卷理科第4题(文科第6题))如图1,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )

图1
A.90πB.63πC.42πD.36π
答案:B.
总结解决此类问题主要是将三视图还原成直观图,再求相应的面积、体积、最值等.
由三视图还原直观图的思路: ①根据俯视图确定几何体的底面;②根据正视图或侧视图确定几何体的侧棱与侧面的特征,调整实线和虚线所对应的棱、面的位置;③确定几何体的直观图.或借助棱柱(常用长方体、正方体)进行观察和分析,确定出几何体的关键点与关键棱,从而作出原几何体.
题型二几何体的面积体积

表四 几何体的面积体积考查统计表
题型二在小题中主要考查几何体的结构特征,进而求出几何体的面积、体积、最值等;或与三视图结合起来考查;或单独考查旋转体的表面积和体积.文科大题第(2)问主要考查点到面的距离、几何体的面积体积,常以锥体为载体.
例2(2018年高考全国卷I文科第18题)在平行四边形ABCM中,AB=AC=3,∠ACM=90°,以AC为折痕将△ACM折起,使点M到达点D的位置,且AB⊥DA.
(1)证明:平面ACD⊥平面ABC;
(2)Q为线段AD上一点,P为线段BC上一点,且求三棱锥Q-ABP的体积.

图2
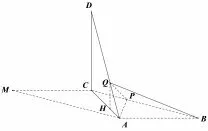
图3
解析(1)由已知可得,∠ACM=90°,故AB⊥AC,又AB⊥DA,所以AB⊥平面ACD.又因为AB⊂平面ABC,所以平面ACD⊥平面ABC.
(2)由已知可得,DC=CM=AB=3,DA=又所以作QH⊥AC,垂足为H,则QH//DC,由已知及(1)可得DC⊥平面ABC,所以QH⊥平面ABC,因为所以所以因此VQ-ABP=×3×3=1.
题型三几何体的切接球问题

表五 几何体的切接球问题考查统计表
几何体的切接球问题一般出现在选择、填空题,属中等偏难的试题.主要考查多面体或旋转体在与球的接或切的背景下,所构成的简单组合体中与球半径有关的计算问题.
例3 (2017年高考全国I卷文科第16题)已知三棱锥S-ABC的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA⊥平面SCB,SA=AC,SB=BC,三棱锥S-ABC的体积为9,则球O的表面积为______.
解析如图4,连接OA,OB.由SA=AC,SB=BC,SC是球O的直径,可知OA⊥SC,OB⊥SC.由平面SCA∩平面SCB=SC,OA⊥SC,可知OA⊥平面SCB.设球O的半径为r,则OA=OB=r,SC=2r,故三棱锥S-ABC的体积所以r=3,则球O的表面积S=4πr2=36π.

图4
总结空间几何体与切接球问题的常用方法
①若球面上四点P,A,B,C中PA,PB,PC两两垂直或三棱锥的三条侧棱两两垂直,可转化为长方体或正方体确定直径解决外接问题.
②球与旋转体的组合,先作它们的轴截面解题;与多面体的组合,通过多面体的一条侧棱和球心,或“切点”、“接点”作出截面图;即把空间问题化归为平面问题,再利用平面几何知识寻找几何体中元素之间的关系求解.
题型四线面位置关系

表六 线面位置关系考查统计表
空间线面位置关系的小题主要考查空间中线线、线面、面面间的位置关系的判定、性质等.大题经常出现在第一问,难度不大,主要以多面体(尤其是棱柱、棱锥)为载体,考查线线、线面、面面三者的平行与垂直关系的证明,特别要关注垂直关系的证明.
例4(2016年高考全国I卷文理科第11题)平面a过正方体ABCD-A1B1C1D1的顶点A,a//平面CB1D1,a∩平面ABCD=m,a∩平面ABB1A1=n,则m、n所成角的正弦值为()

图5
解析如图5,过点A补作一个与正方体ABCDA1B1C1D1相同棱长的正方体,则平面AEF1即为平面a,易知m、n所成角为∠EAF1,因为△AEF1是正三角形,所以
题型五空间角

表七 空间角问题考查统计表
异面直线所成角的考查主要出现在选择题,立体几何理科解答题第(2)问一般考查二面角或线面角,且存在“解法多种,减少计算量”的趋势,因此教师要侧重培养学生的分析能力、逻辑推理能力,合理选择恰当的方法.
1.求异面直线所成角的常用方法有:
2.求线面角的常用方法有:
(1)几何法
(2)向量法:在斜线上取一方向向量a,并求出平面α的一个法向量n,不妨设斜线和平面所成的角为θ,由得到线面角的余弦值.
3求二面角大小的方法主要有:
(1)几何法:直接找出二面角然后计算大小
(2)向量法
下面以线面角为例,介绍几何法和向量法.
例5(2018年高考全国I卷理科第18题)如图6,四边形ABCD为正方形,E,F分别为AD,BC的中点,以DF为折痕把△DFC折起,使点C到达点P的位置,且PF⊥BF.
(1)证明:平面PEF⊥平面ABFD;
(2)求DP与平面ABFD所成角的正弦值.

图6

图7
解析(1)由已知可得,BF⊥PF,BF⊥EF,所以BF⊥平面PEF.又BF⊂平面ABFD,所以平面PEF⊥平面ABFD.
(2)解法一(几何法)
过点P作PH⊥EF,垂足为H,连接DH.由(1)知平面PEF⊥平面ABFD,平面PEF∩平面ABFD=EF,所以PH⊥平面ABFD,故∠PDH就是DP与平面ABFD所成的角.同理AD⊥平面PEF,PE⊂面PEF,所以AD⊥PE.在Rt△PDE中,在△PEF中,PE2+PF2=(2DE)2=EF2,即△PEF为直角三角形.又因为所以所以

即DP与平面ABFD所成角的正弦值为

图8
解法二(向量法)过点P作PH⊥EF,垂足为H.由(1)知PH⊥平面ABFD.以H为坐标原点,的方向为y轴正方向,为单位长度1,建立如图所示的空间直角坐标系H-xyz.由(1)可得,DE⊥PE.又DP=2,DE=1,所以又PF=1,EF=2,故PE⊥PF.可得则H(0,0,0),为平面ABFD的法向量.设DP与平面ABFD所成角为θ,则

故DP与平面ABFD所成角的正弦值为
题型六折叠问题与探索性问题
折叠问题主要考查由平面图形经过折叠在空间中得到立体图形,由这个图形产生立体几何中的基本问题,常与空间中的平行、垂直以及空间角相结合命题,考查学生的空间想象力和分析问题的能力(如2016年全国II卷.文理19、2017全国I卷.理16、2018全国I卷.文理18).
探索性问题常考查探求某些点的具体位置(或是否存在),使得线面满足平行或垂直关系(如2018年全国III卷.文19).
三、学生易错点
1.传统法解题时较常出现的错误:
2.向量法解题时较常出现的错误(理科):
四、备考建议
基于以上立体几何考点的整理与分析,笔者给出以下几点备考建议:
1.注重夯实基础,规范解题过程
立体几何的基本概念、公理、定理是问题解决的基础,要求学生记清概念、理解公理定理,注重通性通法,规范解题步骤,避免“会而不对,对而不全”的现象.
2.建立知识网络,突出动的意识,树立转化思想
在立体几何的复习过程中要让学生注重系统学习,建立完整的知识网络,培养学生“转化”的数学思想.
位置关系之间的转化:

3.重视空间想象,提高图形处理能力
空间想象能力是处理空间图形的基础,空间图形的转化又是解决立体几何问题的关键.在具体要求上,要把握好以下三点:
①培养学生识图、想图、画图、变图、用图的能力(包括规范图形和非规范图形);
②培养学生将概念、性质灵活运用于图形的能力,即数与形有机结合起来;
③培养学生对图形的处理能力,如对图形的折、展、割、补等问题,能够对图形进行分解、组合.

