放缩+最值证一类对称型条件不等式的探究

陕西省岐山县蔡家坡高级中学(722405) 公宽让

对称型条件不等式是指这个不等式左端轮换对称,一般为对称项的和、或对称项的积、或对称项的和与对称式的积的和,其造形优美,证法多样,在高考、竞赛和问题研究中经常出现.这些不等式大多在变元相等时取等号,对在变元相等时取等号的这类不等式,笔者通过研究,发现先放缩,再求最值(简称“放缩+最值”法,以下同)的方法是证明这类不等式的一条捷径.因为它只须研究对称项的性质,所以对比较复杂的这类不等式的证明及推广更显优势.下面是笔者用“放缩+最值”法对这类不等式证明及推广的一些探究.

探究一如果这类不等式的对称项有明显的增减趋势时,可直接考虑用“放缩+最值”法去证.

例1《中学数学教学》2014年第5期有奖征解题

设x1,x2,···,xn都为正数,且x1+x2+···+xn=1,求证：

对(1)的指数作变更,推广如下：

定理1设x1,x2,···,xn都为正数,且x1+x2+···+xn=1,m∈N∗,则

证明不妨设x1≥x2≥···≥xn＞0,则是递减的.由已知x1+x2+···+xn=1,有所以,不等式(2)成立.

当m=n时,不等式(1)成立.

同法可证不等式(1),这里不再重复,以下相同.

例2《数学通报》2017年10月号问题2387

已知a,b,c≥0,且a+b+c=6,证明：

问题2387按元数推广如下：

定理2已知ai≥0(i=1,2,···,n),且则

问题2387按元数和指数推广如下：

定理3已知ai≥0(i=1,2,···,n),且m≥2,m∈N∗,则

证明不妨设a1≥a2≥···≥an＞0,则是递减的,由已知有2≤a1≤2n,当a1=2时,所以,不等式(5)成立.

当m=2时,不等式(4)成立,当n=3,m=2时,不等式(3)成立.

例3《数学通报》2017年4月号问题2356

设a,b,c,d＞0,且a+b+c+d=4,求证：

问题2356按元数推广如下：

定理4设ai＞0(i=1,2,···,n),且a1+a2+···+an=n,则

证明不妨设a1≥a2≥···≥an＞0,则a21+a22+···+a2n+(a2a3···an+a3a4···ana1+···+ana1···an-2+a1a2···an-1)≥na2n+(n-1)an-1n.

令y=na2n+(n-1)an-1n,n≥1,则y=na2n+(n-1)an-1n是递增的,由已知a1+a2+···+an=n,得0＜an≤1.当an=1时,ymax=n+n-1=2n-1.所以,不等式(7)成立.

当n=4时,不等式(6)成立.

例4文[3]猜想：设a,b,c＞0,且a+b+c=1,n≥2,且为整数,则

笔者发现这个猜想是正确的,现按元数推广如下：

定理5设ai＞0(i=1,2,···,m),且n≥2,n∈Z,则

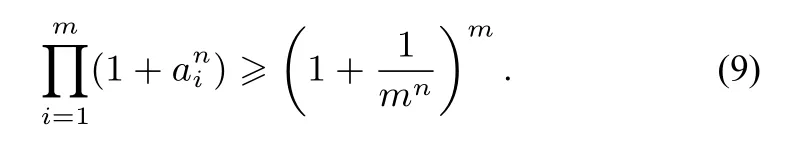
证明不妨设a1≥a2≥···≥an＞0,则(1+ann)m,(1+ann)m是递增的,由已知有时,所以,不等式(9)成立.

当m=3时,不等式(8)成立.

例5《数学通报》2017年12月号问题2398：设a,b,c＞0,a+b+c≤3,求证：

问题2398按元数推广：

定理6设a1,a2,···,an＞0,a1+a2+···+an≤n,则：

问题2398按元数和指数推广：

定理7 设a1,a2,···,an＞0,a1+a2+···+an≤n,p,q∈N∗,则：

证明不妨设a1≥a2≥···≥an＞0,则是递减的,由已知a1,a2,···,an＞0,a1+a2+···+an≤n,有1≤a1＜n,当a1=1时,所以不等式(12)成立.

当n=3,p=1,q=2时,不等式(10)成立;当p=1,q=2时,不等式(11)成立.

探究二如果这类不等式的对称项的增减趋势不明显,可利用函数等方法判定其增减,再用“放缩+最值”法去证.

例6《数学通报》问题1830

已知a,b,c＞0,且a+b+c=2,求证：

问题1830按元数推广如下：

定理8已知ai＞0(i=1,2,···,n),且a1+a2+···+an=n-1,则

证明是递减的,不妨设a1≥a2≥···≥an＞0,则

当n=3时,不等式(13)成立.

例72017年全国高中数学联赛陕西预赛第五题：

设a,b,c为正实数,且满足(a+b)(b+c)(a+c)=1,求证：

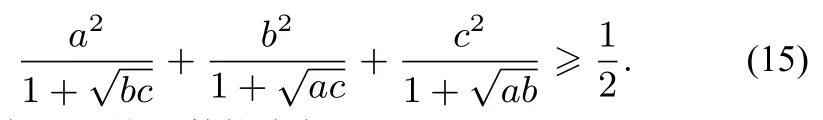
不等式(15)按元数推广如下：

定理9设ai＞0(i=1,2,···,n,n≥3,n∈N),且满足(a1+a2)(a2+a3)···(an+a1)=1,则

不等式(15)按元数和指数推广如下：

定理10设ai＞0(i=1,2,···,n,n≥3,m≥2,n＞m,m,n∈N),且满足(a1+a2+···+am)(a2+a3+···+am+1)···(an+a1+···+am-1)=1,则

证明不妨设a1≥a2≥···≥an＞0,则不等式(17)的左边各项是递减的,从而有

由(a1+a2+···+am)(a2+a3+···+am+1)···(an+a1+···+am-1) = 1,有(man)m≤ 1,得0＜所以,当时,即不等式(17)成立.当且仅当时,等号成立.

当n=3,m=2时不等式(15)成立,当m=2时不等式(16)成立.

例8《数学通报》2017年6月号问题2367

设a,b,c＞0,且abc=1,求证：

问题2367按元数推广如下：

定理11设ai＞0(i=1,2,···,n),n≥3(n∈N+),且a1a2···an=1,则

问题2367按元数和指数推广如下：

定理12设ai＞0(i=1,2,···,n),n≥3,n∈N+,m≥p＞q＞0,且a1a2···an=1,则

证明设则是增函数.不妨设a1≥a2≥···≥an＞0,则由a1a2···an=1,得0＜an≤1.当an=1时,所以,不等式(20)成立.

当n=3,m=3,p=2,q=1时,不等式(18)成立,当m=3,p=2,q=1时,不等式(19)成立.

例9《数学通报》2017年8月号问题2378

设x1,x2,···,xn＞0,x1+x2+···+xn=s,p≥1,求证：

证明令是增函数.不妨设x1≥x2≥···≥xn＞0,则由有当时,所以,不等式(21)成立.

例102009年全国高中数学联赛福建预赛第15题

已知正数a,b,c满足a+b+c≤3,求证：

不等式(22),(23)推广如下：

定理13设正数ai满足m∈N+,则：

证明(i)考察函数是减函数,不妨设a1≥a2≥···≥an＞0,则由已知,1≤a1＜n,当a1=1时,而0＜an≤1,则所以不等式(24)成立.

当n=3,m=1时,不等式(22)成立.

由已知,1≤a1＜n,当a1=1时,所以不等式(25)成立.

当n=3时,不等式(23)成立.

例112015年全国高中数学联赛安徽初赛第9题

设a,b＞0,a+b=1,求证：

不等式(26)按项数推广如下：

定理14设ai＞0(i=1,2,···,n,n≥2),则

证明构造函数所以,上减小,在上增加,是下凸函数.不妨设a1≥a2≥···≥an＞0,由已知当当时,由琴生不等式

(当且仅当x1=x2=__···=xn时取等号),有综上,不等式(27)成立.

当n=2时,不等式(26)成立.

探究三当这类不等式的条件是复杂一点的对称项的和或对称项的积,可用分离或函数等方法去确定范围,然后用“放缩+最值”法去证.

例12《数学通报》2014年9月号问题2201

已知a,b,c＞0,且求证：

问题2201按指数和元数推广如下：

定理15已知ai＞0(i=1,2,···,n)且1(k∈N∗),则

证明不妨设a1≥a2≥···≥an＞0,则而是递增的,由已知1(k∈N∗),有得当所以,不等式(29)成立.

当n=3,k=2时,不等式(28)成立.

小结(1)“放缩+最值”的方法,适合于当变元相等时不等式等号成立的对称型条件不等式的证明及推广;

(2)“放缩+最值”的方法,不同于一般的放缩法,一般的放缩法是适当的同向放缩直到得出要证的结果,技巧性强,弄不好会得到反向结果,使证明陷入僵局,高次的更不好办.这个方法正好化解了这个难点;

(3)人常说：不等式“推广”容易证明难.因为“推广”可以照猫画虎,证明就没那么容易了.“放缩+最值”的方法,不仅可以简捷地证明这类不等式,而且还可以轻松的对这类条件不等式进行推广,并能纠正在推广中由于考虑不周引起的偏差.