解题教学中的逆向思维*

云南省曲靖师范学院数学与统计学院(655011) 孙雪梅

云南省曲靖市第一中学(655000) 李德安

《普通高中数学课程标准(2017版)》中将数学核心素养定义为:学生应具备的、能够适应终身发展和社会发展需要的、与数学有关的思维品质和关键能力[1].如何将数学核心素养落实于课堂教学中是高中数学教学当前要解决的首要问题.数学核心素养本质上反映的是思维品质,基于核心素养的数学课堂教学应立足于学生思维品质的培养[2].

逆向思维是指根据一种观念(概念、原理、思想)、方法及研究对象的特点,从它的相反或否定的方面去进行思考,以产生新的观念[3].家喻户晓的“司马光砸缸”的故事,就是典型的逆向思维,人们习惯的正向思维要从水里救人,是要让人离开水,而司马光的聪明之处就是利用逆向思维让水离开人.在数学中也经常用到逆向思维来破解用正向思维解决起来较为复杂困难的问题,从而得到新颖巧妙而简洁的解法.文中通过例子,对比分析正向思维与逆向思维在数学解题中的应用,并探究如何在数学解题教学中培养学生的逆向思维能力.

1.公式逆用,化繁为简

例1判断函数f(x)=的奇偶性.

利用正向思维要判断函数的奇偶性,学生想到是图象法和定义法,于是可得如下解法1和解法2.

解法1画出函数f(x)的图象,可知图象关于原点对象,f(-x)=-f(x),所以f(x)是奇函数.

解法2根据已知条件,进行分类讨论.①当x≥0时,则-x≤0.f(-x)=(-x)2=x2=-(-x2)=-f(x);②当x≤0时,则-x≥0.f(-x)=-(-x)2=-x2=-f(x).综上所述,f(-x)=-f(x).又f(x)定义域关于原点对称,故f(x)为奇函数.

引导学生逆用绝对值公式|x|=由右到左添绝对值符号,可将f(x)的表达式进行转化,从而易判断出f(x)的奇偶性,避免了解法2中繁复的讨论,由此得到以下解法3.

解法3由于所以f(x)=-x|x|.因为y=-x为奇函数,y=|x|为偶函数,所以显然f(x)是奇函数.

“可逆性”、“双向性”是数学逆向思维最基本的特征,它包括了两个不同而又相互关联的过程,它与只是向着一个方向起作用的单向的A→B型联想(联结)相反,是双向的A←→B型的联想的建立[3].学生习惯正向的“顺思”,而忽视了事物间是互为因果联系的.学生由于思维定势对“反过来”思考的逆向思维不太习惯,但逆向思维对数学问题的解决能起到简化甚至是突破性的效果.通过正向和逆向思维解法的对比,让学生切实感受到逆向思维化繁为简的作用.

2.打破常规,化陈为新

例2若a＞0,b＞0,且当时,恒有ax+by≤1.求以a、b为坐标的点P(a,b)所形成的平面区域的面积.

学生看到线性规划的题,由于思维定势,马上想到是构造目标函数,然后讨论目标函数在约束条件下的最值问题,自然有体现正向思维的以下典型解法1.

解法1作出线性约束条件对应的可行域,如图1所示,在此条件下,要使ax+by≤1恒成立,只要ax+by的最大值不超过1即可,令z=ax+by,则

①当-1即b＞a时,则直线经过点A时z最大,且zmax=b,所以b≤ 1,此时,0＜a＜b≤1,点P(a,b)形式的可行城如图2所示,

综上所述,点P(a,b)所形成的平面区域是边长为1的正方形,如图4所示,故点P(a,b)形成的平面区域的面积为1.

图1

图2

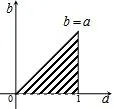
图3

图4

以上解题过程就是正向思维,先设出目标函数z=ax+by,将恒成立问题转化到最值问题,即只需zmax≤1,最后拿出a、b满足的约束条件,求出面积,但为了明确zmax,需要进行分类讨论,较为繁琐而且易出错.引导学生逆向思维:ax+by≤1表示的也是一个平面区域,要使之恒成立,即是一个区域的覆盖问题,简单明了,无须分类讨论即可求出a、b满足的约束条件,即可得到如下解法2.

解法2边界直线ax+by=1恒过点M要使ax+by≤ 1在时恒成立,则ax+by≤1所表示的半平面完全覆盖了所表示的平面区域,所以即故点P(a,b)表示的平面区域是边长为1的正方形,所以点P(a,b)形成的面积为1.

以上逆向思维体现在对数学问题的转换,已知问题A,要解决较困难的问题B,先解决另一个与之相关的较容易的问题C,而解决了问题C也就能解决问题B了.数学中的转换方法离不开运用已有的数学知识、方法和经验来解决数学问题的常规的正向思维.因此,在数学解题训练中,在强调逆向思维的重要性的同时,也要重视正向思维的训练,因为正向和逆向思维虽是不同但又是互相联系的两种思维形式,逆向思维是建立在正向思维的基础上的.正向思维是惯性使然,逆向思维是打破惯性思维,是正向思维的逆向探求和再出发.

3.逆向探求,化难为易

例3 函数y=asinx-bcosx的一条对称轴方程为则直线ax-by+c=0的倾斜角是多少?

学生看到此题,容易想到利用“辅助角”公式,将函数y=asinx-bcosx化为表示出对称轴公式,再将代入对称轴公式进而求出倾斜角的正向思维解法,即是如下解法1.

解法1其中tan对称轴方程为x-φ=∈ℤ,所以+kπkπ,k∈ℤ,所以tanφ=-1,即所以所以倾斜角是

引导学生逆向思维,先不表示出对称轴方程,而是从知道了对称轴方程思考它有什么样的性质出发,从而找到a与b的关系求出倾斜角,有以下解法2、解法3、解法4三种解法.

解法2因为一条对称轴为所以f(0)即-b=a,所以所以倾斜角是

解法3是函数的一条对称轴,所以取得最大值或最小值,所以所以倾斜角为

解法4f(x)在处取得最值也取得了极值,所以因为f′(x)=acosx+bsinx,所以所以所以倾斜角是

以上三种解法就是逆向探求,属于逆向思维中的“反推理”,利用分析法,换个角度看问题,把问题的解决的程序颠倒一下,由结论寻条件,就能化隐为显,化难为易.

4.正难则反,巧妙新奇

例4已知椭圆C:直线l与y轴交于点

P(0,m),与椭圆C交于相异两点A、B,且求m的取值范围.

此题属于直线与圆锥曲线的综合问题,正向思维就是利用常规解法:联立方程、消元、利用韦达定理和“Δ”判别式、,再根据题设条件找到与坐标的联系,于是有以下解法1.

解法1由题意知直线l斜率存在且不等于0,设其方程为y=kx+m(k/=0),代入椭圆方程得(2+k2)x2+2mkx+m2-4=0(*).设A(x1,y1),B(x2,y2),由韦达定理得又即有 (-x1,m-y1)=2(x2,y2-m),所以-x1=2x2,所以所以x1·x2=-2(x1+x2)2,所以⇒(9m2-4)k2=8-2m2.当9m2-4=0时,上式不成立,所以9m2-4/=0,所以＜m2＜4,此时方程(*)中的Δ＞0成立,所以m的取值范围是

解法2可理解为过点P的直线与椭圆交于A、B两点,存在显然当AB⊥y轴时,|AP|=|BP|,故只需≥ 2,当点A、B分别在椭圆的下、上顶点时,取最大值,所以又m＜2,所以由对称性可知,-2＜m也满足题意.所以m的取值范围是

综合法和分析法是数学中常用的解题方法,综合法的思维就是由已知到结论的正向思维,而分析法就是由结论到已知的逆向思维.此题正向思维的常规解法,虽然思路简单,但计算繁琐.在教学中,要适时启发点拨,有意识地培养学生的逆向思维能力,可使学生思维的敏捷性、灵活性、深刻性得到培养和提高.

史宁中在《高中数学课程标准修订中的关键问题》中强调:“数学核心素养是“四基”的继承和发展,“四基”是学生形成和发展数学核心素养的有效载体,强调“四基”就要把握数学知识的本质,在数学教学活动中,让学生在掌握知识技能的同时理解知识的本质,感悟知识所蕴含的数学基本思想,积累数学思维和实践的经验,在这个基础上促进学生形成和发展数学核心素养.”[1]在解题教学中,结合相关例题,让学生掌握逆向思维在数学解题中表现为“反序”、“否定”两种形式,“反序”包括反问题程序、反条件结论法(同一法、待定系数法)、反推理法(分析法、逆证法)和逆用公式、定理和定义等,而“否定”包括求补法、反证法、举反例法等[4].教师在解题教学中要重视公式、定义、定理的逆用,要有意识训练学生会正反面思考,如果正向思维受阻或者较困难繁琐就应考虑逆向思维,正难则反.要让学生通过实例学会反面思考或者从已知的条件、结论的否定方面去探索,或者通过转换问题和方法,反序思考.通过正向和逆向思维的对比,让学生感受到逆向思维化难为易、化繁为简、化陈为新的作用,特别是在使用正向思维百思不得其解,山穷水尽疑无路时,使用逆向思维迎刃而解,体会到柳暗花明又一村的感觉,让学生切实感受到逆向思维的奇妙和新颖.