初中数学规则课关键教学策略探究*

广东省广州市华侨外国语学校(510095) 陈文阳

广东省广州市越秀区教育发展中心(510080) 吴平生

初中数学中的定理、公式、法则、性质和数学基本方法等统称为初中数学规则,我们把以初中数学规则的教学作为主要教学任务的一类课称为初中数学规则课.根据皮连生教授提出的“广义知识学习三阶段模型”,数学规则的学习需要经历新规则的习得、巩固与转化、迁移与应用三个心理阶段,下面结合这三个心理阶段来探究初中数学规则课的关键教学策略.

一、习得数学规则的关键教学策略

1.提供问题情境,自然生成规则.

习得数学规则有两种基本方式:一种是从例子到规则的学习;另一种是从规则到例子的学习.教学中可根据具体数学规则的特点,创设合适的问题情境,让学生动手操作、观察猜想、推理证明,由具体的例子发现数学规则、习得数学规则.例如在“角的平分线的性质”教学中,可创设如下的问题情境.

问题情境1如何画出一个角的平分线?有哪些方法?并说明其依据.

方法1用折纸方法折出角的平分线,依据是角是轴对称图形.

方法2借助量角器画出角的平分线,依据是角的大小可度量.

方法3用尺规作图作出角的平分线,依据是全等三角形的对应角相等.

问题情境2如图1,在∠AOB的平分线OC上任取一点P,如何画出点P到OA,OB的距离?观察点P到OA,OB的距离,两者有何关系?并加以验证.

方法1过点P将平角平分折出垂线段PD与PE.通过折纸重合可发现PD=PE.

图1

方法2借助量角器作出垂线段PD与PE.用刻度尺测量可发现PD=PE.

方法3用尺规作图的方法作出垂线段PD与PE.由三角形全等可证明PD=PE.

以上问题情境从画出一个角的平分线的熟悉情境出发,过渡到画出角平分线上一点到角两边的距离的陌生情境,通过动手操作、几何测量、推理证明等多种方式让学生经历了角平分线性质的生成与发现过程,丰富了学生的数学体验,开阔了学生的数学思维,促进了学生对“如何获得”与“如何验证”角平分线性质的理解和认识.

2.提供多元表征,促进理解规则.

数学规则的教学要让学生明确数学规则为什么是这样,揭示规则背后的数学原理.在数学规则教学中,教师要有意识地提供多种证明或理解方法,展示数学规则的不同表征形式,丰富学生对数学规则的多元认识.

例如,在平方差公式(a+b)(a-b)=a2-b2的教学中,可提供如下的表征形式.

①情境表征:将一块边长为a米的正方形土地一边减少b米(0＜b＜a),相邻一边增加b米,变成一块长为(a+b)米,宽为(a-b)米的长方形土地,问前后土地的面积是否发生了变化?由此引导学生发现公式.

②操作表征:任取几组a,b的数值,分别计算(a+b)(a-b)和a2-b2的值,比较结果,形成猜想,再用多项式乘多项式验证公式.

③文字表征:用文字语言“两数之和与这两数之差的积,等于这两数的平方差”叙述平方差公式.

④符号表征:用符号(□+△)(□-△)=□2-△2理解和记忆公式.

⑤图形表征:利用如图2中图形的面积说明平方差公式.

在给出数学规则的文字、符号、图形等各种表征形式之余,还应分析各种表征的特性及其局限性,帮助学生对数学规则的表征形式作出选择与转换,从而全面理解数学规则.

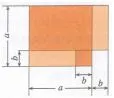
图2

二、巩固数学规则的关键教学策略

1.提供样例学习,明确规则要点.

在数学规则教学中,教师提供样例给学生学习,明确使用数学规则的程序与步骤,是将数学规则转化为办事技能的重要步骤.比如在学习用公式法解一元二次方程时,可提供如下样例.

例1用公式法解下列方程:

①x2+3x-5=0;②4x2-12x+9=0;③x2+15=7x;④x(2x-4)=5-8x.

通过以上样例,让学生明确用公式法解一元二次方程的一般步骤可分为五步:化→写→算→判→求.第一步:化,即把方程化成ax2+bx+c=0的标准形式;第二步:写,即写出系数a,b,c的值;第三步:算,即计算出根的判别式Δ=b2-4ac的值;第四步:判,即根据判别式Δ的符号判断方程实数根的个数,当Δ＜0时,方程无实数根;当Δ=0时,方程有两个相等的实数根;当Δ＞0,方程有两个不等的实数根;第五步:求,即当Δ≥0时,代入求根公式求出方程的实数根x1与x2.样例中题①,②,③的方程根的判别式Δ的符号分别是Δ＞0,Δ=0,Δ＜0,代表了方程不同实根个数的情况,题③,④的方程需先化成标准形式.

2.提供反例学习,突破规则难点.

学生对新规则的理解和使用往往存在着一定的误区,在规则教学中通过展示学生练习或作业中的常见错误,让学生分析错误并反思其根源,可以帮助学生完善对规则的理解,突破规则学习的难点.比如在学习用提公因式法分解因式时,可提供如下反例学习.

例2判断下列因式分解是否正确?若不正确,请指出错误并加以改正.1○a2b-2ab2+ab=ab(a-2b);2○m2(x-y)-m(y-x)=(x-y)(m2-m).

以上反例源自学生常犯错误,通过剖析上述反例,指出漏项、漏变号、分解不彻底等常见错误,进一步总结出比较两边项数、把因式展开对照等检验方法,让学生学会找错、纠错、防错的方法,提高正确运用规则进行因式分解的技能.

三、应用数学规则的关键教学策略

1.提供变式练习,促进规则运用.

学习数学规则的目的是能将习得的数学规则运用到具体情境中去解决相应的问题,进行变式训练是促进学生对数学规则迁移与应用的有效途径.

提供变式练习主要有两种方式,第一种方式是保持规则的本质不变,不断改变非本质属性的呈现形式,使得学生能够灵活运用规则解决问题.例如在学习幂的乘方法则:(am)n=amn(m,n都是正整数)时,可以提供如下例题及变式练习.

例3计算:(1)(103)5;(2)(a4)4;(3)(am)3;(4)[(a+b)2]n.

变式1计算:(1)(x3)4·(x6)2;(2)(x3)4+(x6)2;(3)-(x3)4+(-x6)2.

变式2若am=2,an=3,求a3m与am+2n的值.

变式3若4n·8n=210,求n的值.

变式4比较230与320的大小.

以上例题与变式分别从法则的正用(幂的底数可以是数、字母、单项式或多项式,指数可以是数或字母),混用(同底数幂的乘法、幂的乘方、合并同类项的混合运算),逆用(化为同底数),变用(化为同指数)等角度与方式对幂的乘方法则进行了各种变式,促进了学生对运算法则的深入理解与灵活运用.在解决上述问题时,可以让学生不断思考并回答:本题用到了哪些运算?每一步的运算依据是什么?使学生充分理解具体的算法与背后的算理之间的内在联系.

图3

提供变式练习的第二种方式是适当改变数学规则的条件或结论,得到与原规则相关的命题,引导学生从不同的角度去理解原规则,促进学生对规则的应用.比如,学生由圆的对称性习得圆的垂径定理(垂直于弦的直径平分弦,并且平分弦所对的两条弧)后,教师可以引导学生分析定理的条件(一条直线经过圆心,且垂直于弦)和结论(该直线平分弦,且平分弦所对的优弧或劣弧).通过调换命题的条件和结论可以得到新的命题①:平分弦的直径垂直于弦,并且平分弦所对的两条弧;命题②:弦的垂直平分线经过圆心.然后让学生判断新命题的真假.命题①是假命题,如图3,⊙O的直径CD平分弦AB(AB经过圆心O),但CD不垂直于弦AB;命题②是真命题.接着,可以提供如下的变式练习.

练习1如图4,水平的地面上垂直放置着紧贴在一起的圆圈与刻度尺,刻度尺的宽为2.4cm,它的一边与圆圈的两个交点处的读数分别0和6,求圆圈的半径.

练习2如图5是将⊙O沿弦AB翻折后得到的图形,请用尺规作图的方法找出圆心O(不写作法,保留作图痕迹).

图4

图5

通过对原规则及其相关规则的分析、比较,并加以应用,进一步加强学生对规则的理解,提高学生运用规则解决问题的能力.

2.提供分层练习,促进规则迁移.

数学规则的迁移与应用是一个循序渐进的过程,教师要设计不同层次的练习,强化学生对规则的迁移意识,逐步提高学生运用规则的能力.例如,在学习“勾股定理”后,可设计如下分层练习,有步骤地提升学生应用勾股定理解决问题的水平.

层次一正确叙述规则的水平.

题1判断下列命题是否正确,并说明理由.

①若a,b,c是△ABC的三边,则a2+b2=c2;

②若a,b,c是Rt△ABC的三边,则a2+b2=c2;

③若a,b,c是Rt△ABC的三边,∠A=90°,∠A的对边为a,则a2+b2=c2;

④若a,b,c是Rt△ABC的三边,∠C=90°,∠C的对边为c,则a2+b2=c2.

题1中只有④是正确的.本题旨在检测学生对勾股定理的条件与结论的理解是否有偏差,帮助学生能用符号语言正确叙述勾股定理.

层次二识别规则适用情境的水平.

题2如图6,一根木棒AB斜靠着地面l和墙CDEF放置,已知墙面的倾斜角∠FCD=60°,AC=3米,BC=4米,求木棒AB的长.

图6

图7

题2中的△ABC不是直角三角形,因此不能直接运用勾股定理求AB.如图7,过点B作BG⊥l于点G,构造出Rt△BCG求得CG=2和BG=2,然后在Rt△ABG中利用勾股定理求出AB=本题旨在帮助学生学会识别勾股定理的适用情境,并能适当添加辅助线构造直角三角形来解决问题.

层次三应用规则作出推断的水平.

题3如图8是由一个周长为的六边形ABCDEF与12个不同的直角三角形拼接成的图案,试求a2+b2+c2的值.

图8

这是一道利用勾股定理进行计算推理的题目,由图中已知直角边长可计算出AB=BC=CD=EF=再由六边形ABCDEF的周长可得根据勾股定理则有a2+b2+c2=2019.

题4如图9,在△ABC中,E是中线CD延长线上的一点,∠BCD=45°,∠AED=135°,试探究BC,CD,DE之间的数量关系,并加以证明.

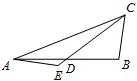
图9

图10

本题需要添加辅助线构造直角三角形,然后利用勾股定理推出相关线段之间的数量关系.如图10,过点B作BF//AE交CD于点F,易证△BFD～=△AED,从而DF=DE,∠BFD=∠AED=135°.由∠BCD=45°,可知△BCF是等腰直角三角形.根据勾股定理有CF=所以CD-DE=CD-DF=CF=

通过不同层次题目的训练,引导学生学会联想、猜想、探究,并能运用勾股定理对结论作出合理的推断或解释,逐步提升学生应用勾股定理解决问题的熟练程度.

教无定法,贵在得法.在数学规则的习得阶段,创设问题情境,提供多元表征,能够将学生聚焦于重要的学习内容上,有助于激发学生探究的好奇心;在数学规则的转化阶段,提供样例学习与反例学习,能够帮助学生从正反两面获得数学规则的使用步骤与注意事项;在数学规则的应用阶段,提供变式练习与分层练习,有助于学生由近及远地迁移应用规则,体现了教师对学生的支架式指导作用.在数学规则的教学实践中,我们可以根据具体教学内容开发、补充、完善、优化数学规则的关键教学策略,不断提高数学规则教学的实效性.