游戏与数学联系的魅力

汤卫红

【关键词】游戏;多连方;核心素养

【中图分类号】G623.5  【文献标志码】A  【文章编号】1005-6009（2019）17-0050-06

【课前慎思】

学完北师大版五下“正方体的平面展开图”后，有学生问我：为什么正方体的平面展开图只有11种？真的找不到第12种吗？我一时语塞，不知如何回答。这个问题一直萦绕在我心头，苦苦思索后我发现：如果找出所有的六连方，再逐一确认它们是否为正方体的平面展开图，不就能解决了吗？那么，六连方一共有多少种呢？我花了半个小时走了不少弯路才研究出来。我想，这个问题让学生自由探究是完全有可能探究出答案的。怎样开发出这节课呢？必须得引导学生从简单的想起，有序探索，分类思考。开发后的实施发现，学生确实感受到了挑战性和趣味性。但我仍觉得单一，因为没有体现“整合数学”的丰富性和联系性。正当我苦思冥想时，看到学生玩古典智力玩具“伤脑筋十二块”，触发了我联结的通道：这不就是五连方吗？游戏的背后正是数学。顺藤摸瓜，我又想到四连方与俄罗斯方块，它们之间天然的联系让我喜出望外。于是，就有了《多连方与游戏》这节课。

【课堂实录】

一、初聊游戏，激趣引疑

师：同学们，你们喜欢玩游戏吗？都喜欢玩哪些游戏？

生：密室逃脱、吃鸡、王者荣耀……

师：网络游戏很容易上瘾哦！咱可以用其他益智游戏来替代哟！

生：魔方、数独、鲁班锁、九连环、俄罗斯方块、伤脑筋十二块……（板书：游戏）

师：真好！这些益智游戏有益身心。同学们刚才提到了俄罗斯方块、伤脑筋十二块，请仔细观察这两个游戏的画面，你有什么发现？

生：它们都是由完全一样的正方形组成的。

师：这样的图形叫作多连方。（板书：多连方与）学贵有疑，你想研究什么问题？

师根据生的回答板书：什么是？多少种？规律？联系？有什么用？

二、体悟策略，有序探索

师：今天这节课，咱们就主要围绕这些问题展开研究。你认为首先要解决什么问题？

生一致决定先研究什么是多连方。师给出一个正方形，指名生贴在黑板上。

师：这是不是多连方？

生（摇头）：不是！

师再给出一个同样大小的正方形，生将两个正方形边与边重合贴在一起。

师：这个图形，咱们给它取个什么名字？

生：二连方。（板书：二连方）

师（把两个正方形摆成顶点相接）：这是不是二连方？

生：不是！必须是边和边重合。

师接着给出三、四、五、六个正方形，生依次摆出。板书：三连方、四连方、五连方、六连方。接下来研究有多少种。

师：这个六连方让你想起了什么？

生：哇！这不是正方体的平面展开图吗？

师：正方体的平面展开图有多少种？

生：11种。

师：那你猜猜，六连方有多少种？

生：肯定不止11种。我记得课上判断时，有的六连方不能围成正方体。我猜有28种。

生（七嘴八舌）：32种、36种、48种……

师（演示课件）：给大家看一眼。（生准备数，师隐去图）

生：这么多，看得眼花缭乱！

师：如果现在让你研究出六连方有多少种，你有什么想法？

有的生表示有點难，也有的表示有信心研究，但担心会乱、重复或遗漏。

师：既然大家感觉研究六连方有点复杂，咱得想想办法。你觉得可以怎么办？

生1：要分类研究，按一定顺序慢慢去找。

生2：我觉得可以倒回去，先研究五连方。

生3：五连方可能也比较难，可以先研究四连方……可以一直退到二连方。

师：同学们真有办法！华罗庚爷爷说过——我们要善于退，足够地退，退到最原始而不失去重要性的地步。二连方有几种？为什么只有一种？

生（操作）：因为旋转后跟横着摆的一样。

师：在数学上，这样旋转以后完全一样的二连方只能称为一种。现在怎么研究三连方？

生：在二连方上添加一个正方形。

师：想一想，三连方有几种？

生纷纷表示有两种，师指名摆出两种。

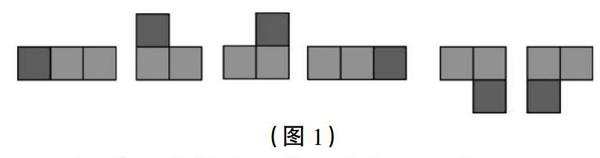
师：为什么只有两种？二连方可以从6个位置“长”出一个正方形。预学时，就有同学画出了这样的6种。（出示图1）

生：第四个图形和第一个相同。第三、五、六个图形都可以通过旋转与第二个图形重合。

师：这里虽然有重复的，但操作方法有什么值得咱们学习的地方？

生：他是从最左边的位置开始有序地沿顺时针方向添加的。

师：为了方便研究和交流，咱们像这样从最左边的1号位开始，沿顺时针方向依次在2号位、3号位……进行添加。为什么从二连方上只能长出两种三连方？咱从二连方这个图形的特征上找找答案。

生：因为二连方是轴对称图形，左右对称、上下对称。

师：接下来，我们再来“长”出——（四连方）。

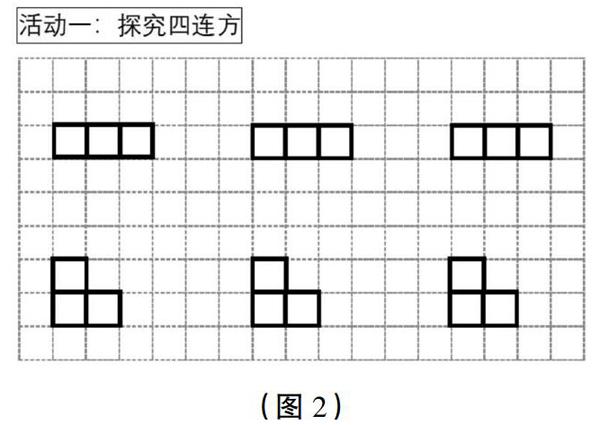
出示共学活动一（如图2）：

（图2）

学生独立完成，4人小组交流，一组汇报。

生1：我们从“一”字形三连方开始添画。从最左边1号位开始，依次画出了3种四连方。由于对称性，从4号位开始就会跟前面的重复。

生2：在L型三连方上，在1号位添画会和上面的第三个四连方重复。在2号位添画没有重复。在3号位添画与上面的第二个图形重复。接着在4号位添画，成为一个田字形。在后面的6号位至8号位添画，也都会重复。

生3：这样，我们一共找到了5种四连方。我想特别强调，大家在画的时候一定要先想想是否与之前的重复，如果重复就不用画了。

生4：大家还有什么疑问或补充？

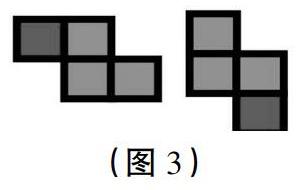
生5：我觉得第二行，在7号位添画应该是可以的，与之前的不重复。

生4：把右边这个四连方逆时针旋转90°，再翻转就和左边的四连方重合了。所以只能算一种。（操作并讲解如图3）

生5：我明白了！我还想到一种更简便的方法，只要通过轴对称就可以证明两个四连方是一样的。（操作演示如图4）

师：为什么在这两个位置添画会重复？你能从三连方本身的特征上找到答案吗？

生3：因为三连方是轴对称图形，而这两个位置正好是对称关系。

三、联系游戏，辨析深化

师：看着四连方，我不禁想起好玩的游戏（板书：俄罗斯方块）。可俄罗斯方块有7种，这是怎么回事呢？结合游戏规则想想。

生2：游戏规则中只有平移和旋转两种运动，没有翻转。所以，L与J、Z与S都必须出现，否则就没办法铺满平面。（如图5）

师：为什么俄罗斯方块中没有出现与I、T、O这三种四连方形状一样、方向不同的图形呢？

生：因为它们都是轴对称图形，即使方向变了，通过旋转也都能和原来的重合。

四、深化探索，挑战思维

出示共学活动二（如图6）：

学生独立探究后小组交流，一组汇报。

生1：我们在“一”字形四连方上依次从1号位开始添画，共有3种。到4号位时就开始与前面的重复了，不用再画了。

生2：在L形上添画，1号位与上面的第三个五连方重复。在2、3、4、6号位添画都出现了新的五连方，在7号位上添画与第一行的第二个五连方重复。再在8、9、10号位上添画。共可以画7个五连方。

生3：在T形上添画，只能找到十字形这一种五连方，其他的都重复了。

生4：在Z形上添画，也只能找到W形一种。而在田字形的每个位置添加都一样，且与第二行的第二个五连方重复。这样，我们一共找到了12种五连方。

生1：我想强调，一定要注意有序，否则就容易遗漏。当然，我们发现越到后来重复得越多，越要仔细检查是不是重复。

生5：我有质疑，我觉得在T形右下角位置添画与之前的不重复。

生2：我可以驗证给大家看。右边的五连方逆时针旋转180°就会跟左边的重复了。（如图7）

生6：在Z形下方添画得到的五连方，我觉得也是重复的。

生5：这个我看出来了，先顺时针旋转90°再翻转，就和刚才的重复了。

生7：我觉得可以更简单，通过轴对称就能发现重复。（如图8）

师：为便于记忆，有人把五连方形象地看成12个英文字母，看一看，是哪12个？

生：哇！正好是26个字母中的后12个。

师：五连方让我们想起的游戏是——（伤脑筋十二块）

师：五连方跟伤脑筋十二块完全一致吗？

生：完全一致，都由12个正方形组成。

师：游戏规则跟俄罗斯方块有什么不同？

生：伤脑筋十二块允许翻转，因为在拼图时是可以翻过来拼的。

师（出示拼图）：咱们来验证一下，看看这两幅拼图中的同一个形状是不是翻转了。

生（演示）：这一块就用了翻转。

师：假如伤脑筋十二块不允许翻转，哪些形状需要给出另外一种？

生：P、Q、R、S、Y、Z这六种需要给出它们的轴对称图形。

师（出示图）：研究了半天，我们再来看看俄罗斯方块与伤脑筋十二块这两种拼图游戏，其实都与哪一个数学知识有关？（密铺）

师：我们已经研究了什么是多连方、有多少种、它们之间的关系及其与游戏的联系，你还想研究什么？

生：我想研究有什么规律，这样我们就可以推断六连方有多少种了。

师：仔细观察黑板上这张表，你有没有发现什么规律？

生1：我发现n连方的个数=（n-1）连方的个数的2倍+（n-2）连方的个数。比如，四连方的个数就是三连方个数2乘2加二连方个数1，共5个;五连方的个数就是四连方个数5乘2加三连方个数2，共12个。

生2：这么看，六连方应该有12×2+5=29个。

师：真是这样吗？咱们得——（验证）

师：这个研究起来比较复杂。我们可以先对这12种五连方——（分类）能分成哪几类？

生：一字形一类、1+4一类、2+3一类、1+1+3一类、1+3+1一类，1+2+2一类。

师：由于这个工作量非常大，现在咱们来分工合作探究。4人小组分成两个2人小组，分别完成3个五连方基础上的“生长”。

出示共学活动三（如图9）：

学生合作探究后全班交流，一组重点汇报。

生1：在一字形上添画，从1号位到4号位有4种，从5号位到10号位就与之前的重复了。

生2：1+4类，第1幅图可以在2、3、4、6、7、9、10、11、12号位添画，共有9种;第2幅图可以在4、5、10、11号位添画，共4种。这样我们两人就找到了17种。

生3：2+3类，第1幅图可以在1、3、4、5、6、8、9、10、11、12号位添画，共10种。但在1、8号位添画与第1小组的重复了，我们划掉了。所以，只有8种。

生4：2+3类，第2幅图可以在1、3、4、5、8、9号位添画，但在1号位添画与第1小组的也重复了，共5种。第3幅图可以在1、3、10、11号位添画，但1号位添画与第1小组的也重复了，共3种。我们两人共找到16种。

师生针对有质疑的图形进行验证交流。

师：六连方的探究才进行了一半，但我们已经可以推翻刚才的猜想了。

生：是啊！已经33种了，刚才的规律不灵了。 师：其实，探究看似才进行了一半，但胜利的曙光已近在咫尺。观察图形的特征，想一想，哪类图形可能已经“生长”不出不一样的六连方了？

生：我觉得1+3+1这一类可能已经“生长”不出了。我随意试了几个，都重复了。

师：确实如此，现在咱们只有在L形、W形上找答案了。这两种五连方各自只能长出一种不重复的六连方了，猜猜可能是哪两种。

出示所有六连方图（如图10），学生欢呼。

师：现在，咱们确定六连方共有35种，可以尝试回答为什么正方体只有11种展开图了。

生：只要逐一验证哪些六连方能围成正方体就可以确认了。

五、畅谈收获，延伸拓展（略）

【课后反思】

数学的教育功能不只在技术与工具层面，还在于文化熏陶与人格培塑层面。数学中蕴含的理性精神、积极情感、审美旨趣、文化意识、文化品格等都应当成为数学教育的价值取向。“整合数学”的课堂追求在育人高度上考量学科内、学科间、超学科的联系与整合。本課在以下三个方面作出了努力：

第一，以多连方为载体，将数学内部的图形变换知识一体化应用，设置具有挑战性的任务，促进学生空间观念的深度发展。平移、旋转、轴对称等变换，在探究多连方有多少种、辨析是否为同一种、分辨游戏与多连方的联系与区别中都得到了丰富而灵活的应用。这是在小学阶段全部学完几种变换后的一次综合应用，如何使学生基于已有经验实现再发展是本课教学一个重要目标。我试图基于操作并超越操作，遵循能想象不操作、能推理不操作的原则，充分调动学生观察、想象、推理、验证的积极性。当然，在模糊的地方还是要以实际操作来验证。同时，注意引导学生深入理性分析层面把握图形特征，为其想象图形的位置关系、运动和变化提供有力的依据。在学生表达的过程中激发其他学生依据描述想象和理解，也旨在促进他们进一步发展空间观念。

第二，在思想方法上，突出有序、分类、简化等的一致性，促进学生形成“带得走”的思考力。在实践中，我欲擒故纵，面对挑战性较强的问题，启发学生自主寻找简化的策略，在抓住基本操作方法的基础上不断迈进，一步步体验成功，感悟“生长”的力量，自然体会到分类思考、各个击破、纵横比较的益处。探究过程中的有序思考、分解散点、小心验证都让学生体会到思想的巨大能量，在“纵向数学化”的道路上享受到柳暗花明、乘胜追击、大胆猜测、求证纠错的高峰体验。

第三，打通游戏与数学的联系，引导学生在“横向数学化”的世界里自由穿梭，体会数学在游戏创造和规则设计中的价值。在课的高潮部分，学生发现原来游戏背后真的是数学，且由于规则的需要，数学的简洁、抽象需要做一些让步，学生惊叹于这种联系和区别。实践表明，学生课外对七连方、八连方及其相关拼图游戏的热衷更彰显出数学与游戏打通的巨大魅力。数学眼光、普遍联系、模型应用等思想或意识也正潜移默化地成为学生素养的一部分。