考虑不确定性因素的不锈钢点焊车体焊点强度评估

智鹏鹏,李永华,陈秉智

(1.大连交通大学 机械工程学院,辽宁 大连 116028; 2.大连交通大学 机车车辆工程学院,辽宁 大连 116028)

为了适应轨道交通装备高强度和轻量化的设计需求,不锈钢点焊车以其抗冲击、抗温升、耐腐蚀、自重和维护运营成本低等优点越来越受到业界的关注[1].然而,不锈钢因其独特的材料特征,在焊接过程中易发生热变形.因此,为获得较好的焊接质量,减少焊接变形,不锈钢车体的各类薄壁梁结构采用热输入量较小的电阻点焊连接[2].在设计阶段主要通过有限元计算其刚度和静强度，验证不锈钢车体是否满足标准要求.但是,在有限元分析结果中各设计参数均为确定值,而实际加工过程中存在较多不确定性因素,导致实验与分析结果具有一定的差异.在设计阶段焊点的静强度评估是保证列车运行过程中焊点不发生开裂的基础和前提,而国产不锈钢点焊车体较少评估焊点强度和疲劳寿命,致使焊点存在开裂的风险[3].因此,考虑车体加工和焊接过程中的不确定性因素评估焊点的静强度,对预防焊点开裂,保证车辆安全、可靠运行具有重要的指导意义.

目前,针对不锈钢点焊的研究,许娇等[4]根据EN 12663:2010标准分析了全自动不锈钢车体的静强度和模态,验证了车体结构设计的合理性.束洋[5]基于ABAQUS软件分析了焊缝长度和间距对激光断焊结构性能的影响,并根据疲劳性能对激光焊的位置进行了布局优化,获得了具有优良疲劳性能焊缝的焊接原则.谢素明等[6]通过对焊点位置的布局优化研究了不锈钢车体的屈曲问题,分析了焊点位置对结构稳定性的影响.姚亚涛[7]对9种焊点的模拟方法进行了对比分析,得到了两种较优的焊点模拟方案,并通过对车体进行分析,验证了方案的可行性.孙芳芳等[8]采用ANSYS软件分析了201不锈钢电阻点焊的温度场和应力场,并通过试验测定，验证了模拟结果的准确性.

上述研究分别从不锈钢车体、点焊过程的模拟和焊点的布局等方面进行了分析,并未涉及焊点强度的评估.在设计阶段为了提高车体焊点强度评估的准确性,本文以某型号不锈钢点焊车体为研究对象,考虑加工制造和焊接过程中的不确定因素,建立了参数化的车体有限元模型,并结合D-最优试验设计和AWS C1.1M/C1.1:2012(AWS)标准编写的综合剪切强度Tcl脚本文件,建立了设计参数与焊点强度的函数表达式.基于证据理论确定了样本点在各设计区间的基本可信度分配(Basic Probability Assignment,BPA),据可靠性理论分析了焊点强度的可靠性.该方法对准确评估焊点强度是否满足要求具有参考作用,且符合工程实际.

1 不锈钢点焊车体设计参数的选取

设计参数的不确定性是载荷、材料、尺寸公差和制造工艺等不确定性因素综合作用的结果.针对焊点强度而言,并非所有的设计参数均对其有影响,因此,选择合适的设计参数是准确评估焊点强度的前提.

本文选取的不锈钢点焊车体由底架、端墙、侧墙和车顶4部分组成,各部分主要通过焊点连接.车体总体采用Shell181壳单元进行网络划分,单元总数为1 169 876个,节点总数为1 206 010个.各吊装设备采用Mass21单元以质量点形式施加,并通过Rbe3连接到相应位置.焊点作为车体传力的主要部位,其尺寸相对车体较小,与车体的关系可视为“点传力结构”.对这类结构,常采用具有轴向拉压,弯曲和扭转特性的梁单元Beam188单元进行模拟.不锈钢点焊车体的焊点模拟如图1所示.

图1 不锈钢点焊车体焊点模拟Fig.1 Welding spot simulation for stainless steelspot welding car body

根据EN 12663-1:2010标准,车体垂直载荷工况为(整备状态下的车辆自重-两转向架重量+超员AW3)×g×1.3,并在空气弹簧处施加约束[9].车体的主要材质为SUS301L不锈钢,牵枕缓和底架边梁为碳钢,不锈钢点焊车体的应力云图，如图2所示.

由图2可知：车体最大应力为293.2 MPa,发生位置为窗上外板,该部位材料的屈服强度为345 MPa,满足标准要求.图2显示,车体侧墙受力较大,该位置的焊点布置也较为密集,因此,将侧墙的外板、窗立柱、门立柱以及侧墙横梁的板材厚度作为主要的设计参数,同时考虑点焊过程中的不确定性,将其所对应焊点的焊核直径也作为主要的设计参数.

图2 不锈钢点焊车体应力云图Fig.2 Stress plot for stainless steel spot weldingcar body

2 基于不确定性的焊点强度评估

2.1 焊点综合剪切强度的计算

焊点强度的评估实质是评估焊点的综合剪切强度是否满足标准要求,由于利用Beam188单元模拟焊点,因此,需要对该单元的性质进行分析,计算并提取出单元的综合剪切强度.Beam188单元的三维及断面的力学性质描述如图3所示.

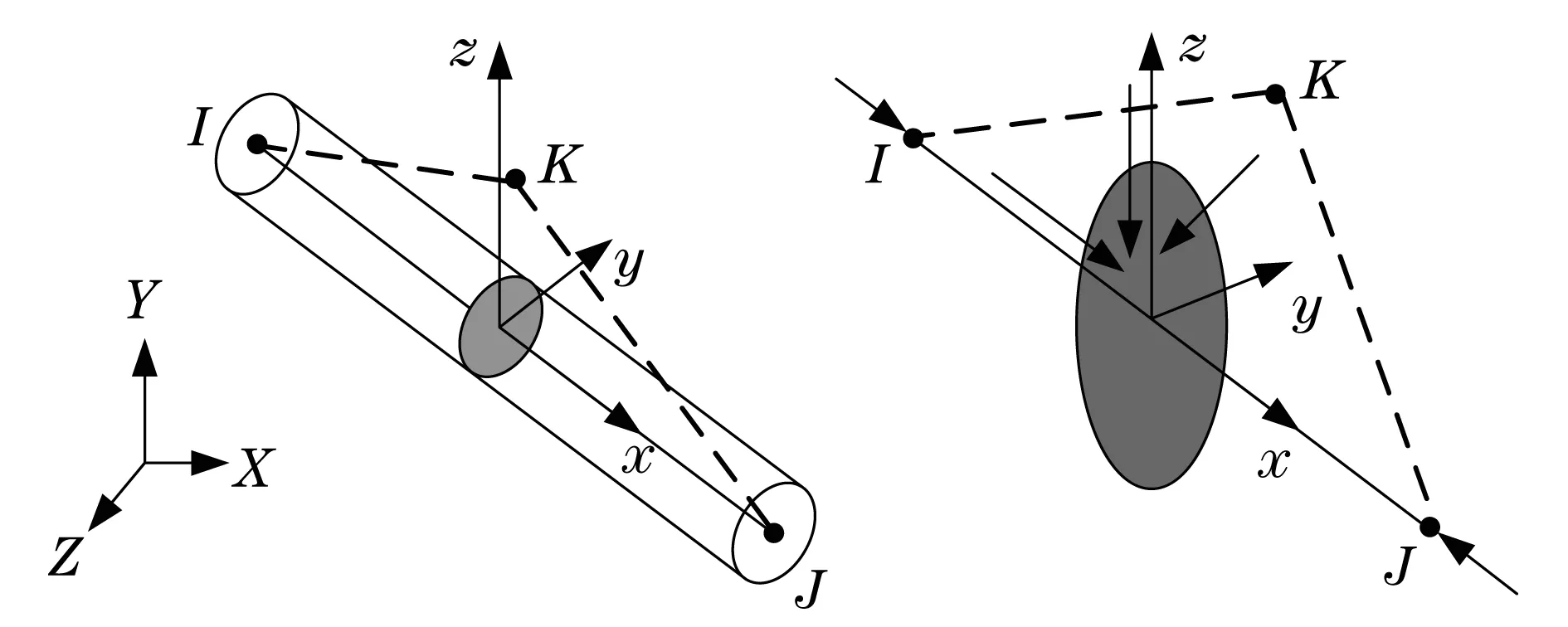
图3 Beam188单元Fig.3 Beam188 element

由图3可知：该单元主要受轴向力Fx、剪切力τy和τz.在有限元分析中对应的APDL为SFz=SMISC(5)和SFy=SMISC(6),根据力的合成规则,Beam188单元受到的综合剪切力为

(1)

2.2 基于美国焊接标准的焊点强度评估

国内对焊接部件的评估标准通常参考EN 15085-3:2007[10].该标准详细地介绍了铁路车辆焊接部件的设计要求、缺陷质量等级和焊接接头的设计等内容.该标准对电阻点焊的评估是基于最低剪切拉应力,同时根据不同的焊接性能等级查表得出所对应的焊点最低剪切拉应力.美国焊接学会(American Welding Society,AWS)C1.1M/C1.1:2012标准[11]也同样基于最低剪切拉应力给出了不同的焊接性能等级所对应的最低剪切拉应力.文献[12]认为两种标准具有较大的相似性,可用于评估不锈钢点焊车.但AWS明确标注了点焊的材料范围,通过对比发现目标中SUS301L不锈钢对应美标中的301不锈钢,因此,可将AWS标准用于该型号地铁车的焊点强度评估.评估所用的不锈钢点焊的参数如表1所示.

表1 不锈钢点焊参数Tab.1 Spot welding parameters for stainless steel

表1给出了焊接薄板厚度所对应的最小剪切强度值.由表1可知,薄板厚度并不具有连续性,应通过插值求得侧墙厚度所对应的焊点的最小剪切强度.本文采用的方法为梯形插值,如图4所示.

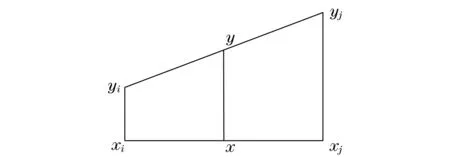
图4 梯形插值示意图Fig.4 Trapezoidal interpolation diagram

设侧墙焊点所连接的两块板材中薄板的厚度为x,在表1中查得x的上、下限分别为xi和xj,所对应的最小剪切强度为yi和yj,则x所对应的最小剪切强度y为

(2)

侧墙的主要材质为SUS301L(HT)和SUS301L(DLT),两种材料的最低抗拉强度为690 MPa.因此,选择表1中的620～1 033 MPa的评估区间.将计算得到的最小剪切强度的0.65倍作为许用剪切强度,并与式(1)求得的τ值作商,即τ/R,得到焊点强度的最大利用率W,若W>1,则焊点强度不满足标准要求,否则满足要求.

2.3 剪切强度和不确定性设计参数函数表达式的建立

为了提高分析效率,本文采用D-最优试验设计选取不确定性设计参数的样本值,其回归模型为

(3)

式中:xα为给定的因子区域X中一点,若因子空间为P维欧氏空间,则xα为P维向量(xα1,xα2,…,xαp);f1(xα),f2(xα),…,fm(xα)为连续函数;β1,β2,…,βm为m个待定系数;εα为服从正态分布的随机变量.

若试验方案是由N个试验点x1,x2,…,xN组成,则可以得到式(1)的参数估计为

(4)

信息矩阵为

(5)

D-最优设计就是使得信息矩阵的值达到极大化的一种设计.

根据第1节确定的设计参数,并考虑其实际生产过程中的上下偏差,利用D-最优试验设计选取样本点,不确定性设计参数应根据试验设计分为3个水平,如表2所示.

表2 不确定性设计参数的水平特征Tab.2 Horizontal characteristics of uncertaintydesign parameters

基于第2.2节的评估方法,利用Tcl语言编制HyperMesh脚本文件,提取焊点强度和最大利用率作为响应,试验设计过程如表3所示.

表3 试验设计过程Tab.3 Process of experimental design

通过D-最优试验设计,得到78组设计参数波动下的焊点的剪切强度和最大利用率,如图5所示.

由图5可知:考虑设计参数的不确定时得到焊点的剪切强度和最大利用率均有所波动.图5中的剪切强度表示焊接厚度为0.8 mm的外板加强梁和1.5 mm的侧墙外板间所有焊点强度的最大值.由于参数的不确定性导致焊点强度的最大值为2.46 kN,对应的最大利用率为0.9.由此可见,不确定因素的存在很可能使焊点强度超过标准值.

图6给出了焊接厚度为1.0 mm的窗、门立柱与1.5 mm的侧墙外板间所有焊点强度的最大值及其最大利用率.

图5 TH1～TH3焊点的剪切强度和最大利用率Fig.5 Shear strength and maximum utilization ofwelding spot for TH1～TH3

图6 TH2～TH3焊点的最大利用率Fig.6 Maximum utilization of welding spotfor TH2～TH3

由图6(a)可知,焊点强度的最大值在78组观测数据中均不符合标准要求,最大利用率在8.2左右波动,说明该点的焊点强度较标准要求高得多,该点在车辆运行过程中极易开裂.图6(b)为第9次试验中TH2～TH3厚度之间所有焊点的最大利用率,在2 070个焊点中,仅有39个焊点的最大利用率大于1,说明焊点强度的分析结果不符合标准要求的判定,并非针对所有的焊点,而是仅指焊点强度中的最大值.因此,若焊点强度的评估不符合标准要求,应提取焊接件间所有焊点的强度,找到不符合要求的焊点,对其进行结构改进,从而避免因设计缺陷导致的车体运行过程中的焊点开裂.

对表3中提供的试验数据进行回归分析,得到不确定性设计参数与焊点强度、最大利用率的回归方程,其表达式为

为了验证回归方程的拟合精度,图7给出了方程的残差曲线.

图7 残差曲线Fig.7 Residual curve

图7可知：焊点强度的残差除了4个点比较突出以外,其余74个点的残差均控制在0.2以内,且大部分处于0.15以内.最大利用率的残差除了1个点比较突出以外,其余各点均在0.02左右波动.说明在给定置信度的前提下,可认为两者的拟合精度较高.

为了直观地观测不确定参数对响应的影响,选取厚度TH1,TH2和最大利用率W,通过最小二乘法拟合响应面,如图8所示.图8给出了板材厚度TH1和TH2的变化对焊点最大利用率的影响.

图8 响应面图Fig.8 Response surface diagram

由图8可知：随着板材厚度的增加,最大利用率减小,说明板材厚度的增加会使焊点强度减小.

2.4 不确定性设计参数样本点选取的BPA

在考虑设计参数等不确定性因素的基础上,为了进一步减少焊点强度评估的不确定性,需同时考虑认知不确定性对评估结果的影响,本文采用证据理论处理板材厚度和焊核直径落在区间范围的不确定性.

证据理论又称为D-S理论[13],由Dempster和Shafer首先提出,并被广泛应用到认知不确定分析领域.分析所涉及的证据理论的基本概念如下:

(1) 识别框架(Frame of Discernment,FD).

对于某一决策问题,人们认知的所有可能结果组成的完备集合,且集合中的所有元素两两互不相容,在某些情形下,事件发生仅为集合中的某一元素,这样的集合称之为识别框架,用符号Θ表示，即

(8)

式中:xi为识别框架Θ中的元素;n为元素个数.

(2) 基本可信度分配(BPA).

BPA描述了证据的可信程度,设Θ为识别框架,从集合2Θ→[0,1]的映射m称为BPA,其中2Θ为Θ的幂集.需满足以下3个性质:

(9)

式中:A为识别框架Θ幂集中的任意元素;m(A)为BPA,m(A)>0的区间A称为焦元,反映了证据命题A的可信程度[14].

(3) Dempster 合成法则.

假设从不同专家处得到对同一变量X的BPA为m1和m2,所对应的命题分别为B和C,则合成的BPA为

(10)

其中，

(11)

式中:K为不同专家之间证据的冲突程度,冲突越大K越大.

综合各个设计参数在实际生产中的不确定性,两位专家给出了关于板材厚度和焊核直径落在区间范围的具体信息,并通过式(10)合成得到合成后的BPA,如图9所示.

2.5 焊点强度的可靠性分析

焊点强度的可靠性分析是为了验证由设计参数的不确定性引起的结构强度能够达到标准要求的能力.根据可靠性理论[15],焊点强度可靠性评估的极限状态方程定义如下:

(12)

图9 不确定性设计参数的BPAFig.9 BPA of uncertainty design parameters

式中:W为焊点强度的最大利用率;屈服强度为标准要求的最小剪切强度.

根据式(12),可靠度可定义为

(13)

式中:n为κ≤0的次数;N为总样本点数.

利用Matlab 2015b按照2.4节计算的各个区间的BPA,对各个不确定性设计参数的区间随机抽取100个样本点,并进行1 000次随机组合,带入式(7)得到焊点强度的最大利用率样本历史.

图10 焊点强度的样本历史Fig.10 Sample history of welding spot strength

图10展示了1 000次计算的焊点强度最大利用率的分布历史.由图10可知:最大利用率主要集中在0.3～0.6与0.7～0.8之间,最大值与最小值之间大约相差0.5的最大利用率,说明设计参数的不确定性对焊点的强度影响较大.根据式(12)和式(13)可知,焊点强度的可靠度为1,说明0.8 mm的外板加强梁和1.5 mm的侧墙外板间所有焊点强度均符合标准要求.相比确定性的焊点强度分析,不确定性分析结果更能保证车辆量产后的可靠性,同时减少由设计缺陷和分析局限性造成的车辆使用过程的焊点开裂问题.

3 结论

(1) 提出了基于AWS C1.1M/C1.1:2012标准的焊点强度评估方法,并给出了具体的评定过程.相比利用EN 15085-3:2007标准,该方法适用的板厚评定范围更广,评定结果更加精准.

(2) 将有限单元法和D-最优试验设计相结合，分析焊点强度的不确定性,展示了焊点强度随不确定性设计参数变化的总体趋势,同时提高了分析效率.

(3) 基于证据理论的样本点选取规则,相比随机取点,更多地考虑了制造工艺和人为的不确定性,计算结果更具参考价值.

(4) 焊点强度的可靠性分析方法为在设计阶段合理地设定焊点的安全系数提供了理论支撑.