汽车拨叉加工变形超声振动矫形机构设计

孔宪玉

(巴音郭楞职业技术学院 机械电气工程学院,新疆 库尔勒 841000)

随着“中国制造2025”的提出,整个制造行业得到了飞速发展,汽车行业也是如此,各零部件的加工过程也日趋自动化.拨叉是汽车变速箱的关键零部件之一,属于外形复杂的非标类薄壁件,它的加工精度会影响整个变速箱的性能,甚至会缩短汽车的使用寿命.拨叉当前采用的还是较为传统的加工工艺,在加工过程中因多次装夹、切削等工序而易发生永久性的弹塑性变形.目前,国内主要依靠工人根据自己的经验手工矫正,缺乏系统的、具有针对性的矫正理论,受人的情绪影响很大,因此，会对拨叉的矫正稳定性产生很大的影响[1-2].

为了使零部件的加工形变量在控制范围之内,海内外诸多专家学者通过优化生产工艺、设计更加合理的夹具等,希望在生产过程中最大限度地控制变形量.但由于生产环境不佳、设备的加工误差等许多外在因素,拨叉在生产过程中依旧会产生塑性变形.

在传统加工技术中，常用的矫正方法并不普遍适用,矫正的准确性也不高,而超声振动可以利用振动消除拨叉的残余应力,提高拨叉内部应力场的平衡稳定性,防止其产生二次变形[3-4].

本文首先在弹塑性理论基础上,得到了拨叉的横向和纵向变形曲线,建立了相应的修正数学模型;然后基于矫正数学模型,利用Solidworks建立了超声振动矫形机构;最后通过有限元分析软件对超声振动矫正机构的谐响应进行了分析,验证了矫正机构设计的合理性,从而提高了变形拨叉的矫正效果[5].

1 拨叉变形矫正原理分析

1.1 拨叉变形规律分析

在加工过程中,拨叉很容易产生非线性弹塑性变形.在受力加载过程中,拨叉内部的应力平衡会被打破,先产生可逆的弹性变形,当载荷卸载后拨叉即可恢复原状而不产生变形.当外部载荷超过拨叉的屈服极限Fe时,此时拨叉为使内部应力场重新达到平衡状态,便会产生不可逆反的塑性变形.卸载后,拨叉会产生一定量的塑性变形δ0,详细的弹塑性变形原理如图1所示[6-7].

图1 弹塑性变形原理图Fig.1 Elastic-plastic deformation principle diagram

为了了解拨叉在不同维度的变形规律,利用有限元仿真分析,在叉脚末端X方向和Y方向分别施加多组不同的载荷,如图2所示.

根据有限元分析结果,利用Matlab绘制了叉脚末端X向和Y向的变形规律曲线,如图3所示.从图3中可以明确得出,无论是X向或Y向的变形均符合图1所示的弹塑性变形原理,属于典型的非线性弹塑性变形,而且获得的拨叉在X向和Y向的变形趋势是互不相同的.

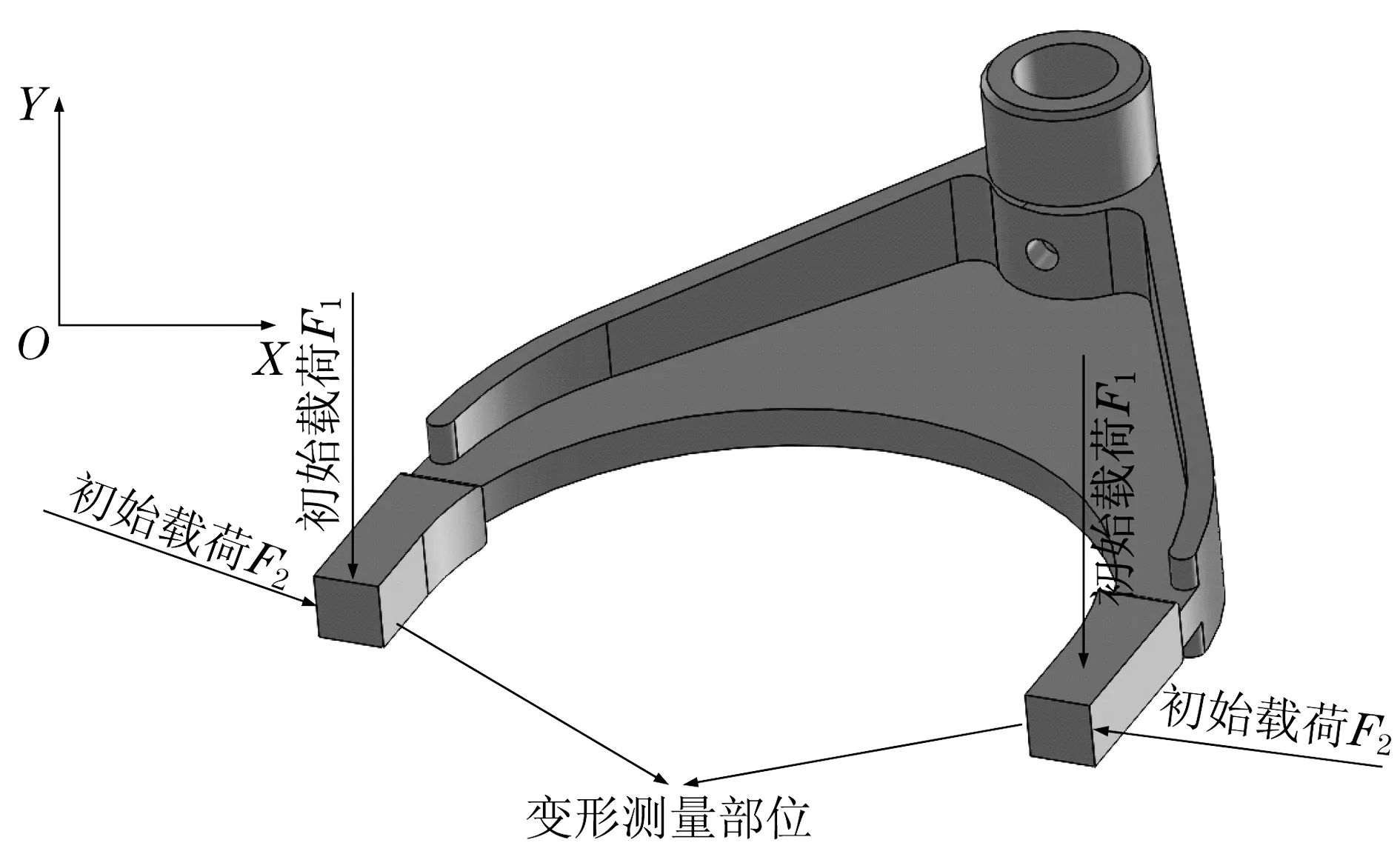
图2 拨叉加载示意图Fig.2 Dial yoke loading diagram

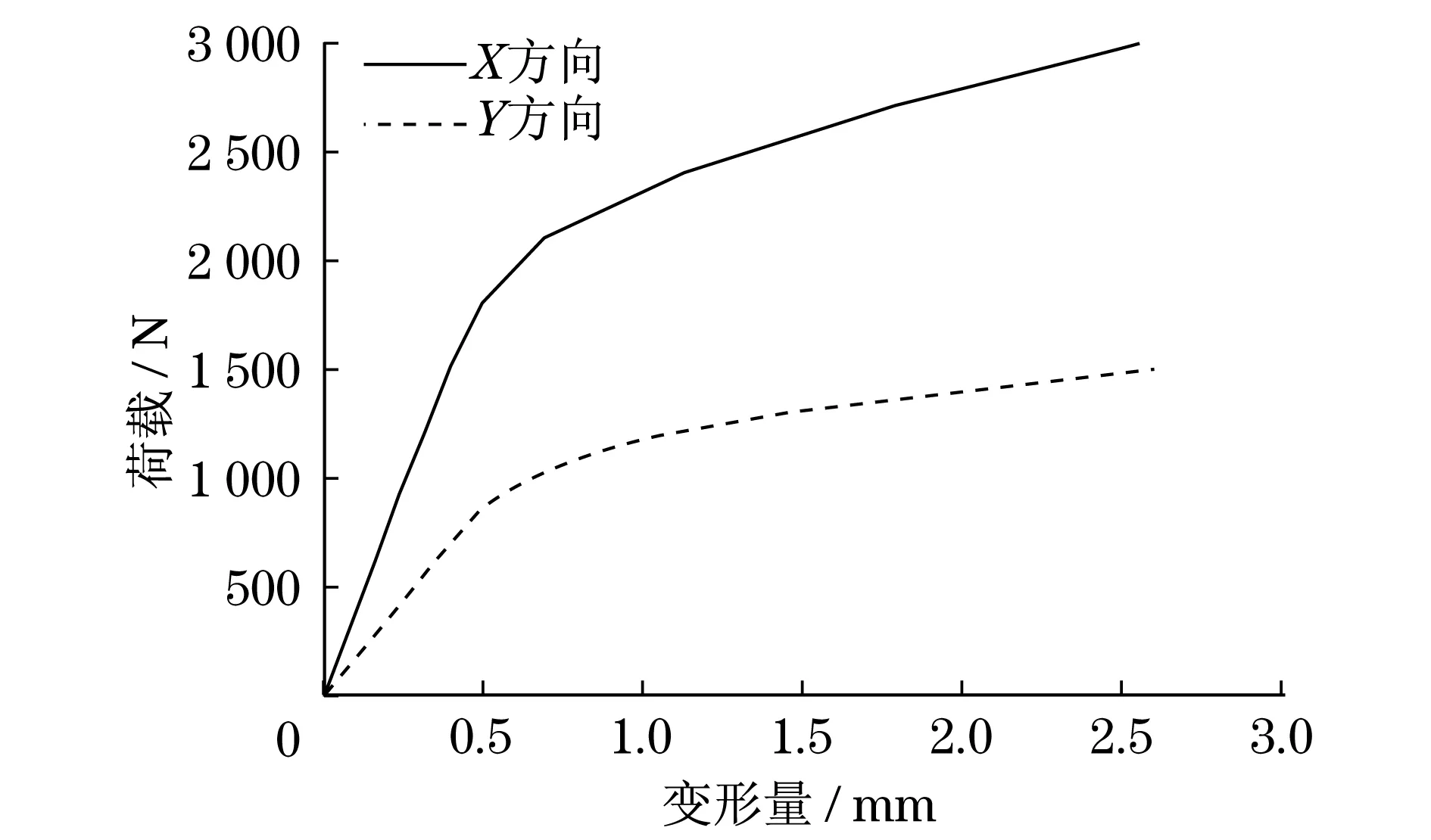
图3 拨叉变形规律曲线图Fig.3 Curve diagramof the deformation law ofdiagonal yoke

1.2 拨叉弹塑性变形矫正模型的建立

在图1中,变形拨叉的矫正过程与变形过程相似,OE是拨叉的弹性变形阶段,且E点是拨叉的屈服极限.当载荷超过E点,拨叉便进入了EC塑性变形阶段,假设拨叉的外部载荷在C点卸载,进入卸载阶段CA,通常假设卸载路径与加载路径相似,并且是一条直线,即CA与OE平行,此时便会产生一个变形量δ0.利用此原理可对拨叉的变形进行矫正,向拨叉变形的反方向施加一个载荷,使其产生一定量的反向变形,如果拨叉的反向变形量与δ0相等,则该载荷就是拨叉的矫正载荷.整个变形矫正过程可用数学模型表示为

(1)

式中:k为弹性变形过程中的斜率;Fe为屈服极限;Fm为矫正载荷.

拨叉在不同维度的变形规律略有不同,因此,其在不同方向的矫正数学模型是有差异的,下面将对X向和Y向的变形矫正数学模型进行分析求解.

拨叉在X向和Y向的弹塑性变形存在一定的差异,因此，其变形矫正模型也是不同的.为了获得相应的变形矫正数学模型的方程,实测了某传动公司某个系列拨叉X向和Y向在不同外载荷下的变形量、残余变形量,并用Matlab对相应的F-δ曲线进行了拟合仿真,如图4和图5所示.

依据图4可以得到拨叉X向塑性变形的数学模型为

(2)

当拨叉的初始变形量为1.105 mm时,则对应的卸载直线方程为

(3)

联立式(2)和式(3),求得对应的矫正载荷F=2 733.49 N，矫正行程δ=1.807 mm,与实验结果F=2 734 N,δ=1.810 mm非常相近,误差非常小,验证了X向变形矫正力数学模型的准确性.

图5 Y向塑性变形曲线Fig.5 Y-directional plastic deformation curve

依据图5可以得出拨叉Y向塑性变形的数学模型为

(4)

当拨叉的初始变形量为1.769 mm时,则对应的卸载直线方程为

(5)

联立式(4)和式(5),求得对应的矫正载荷F=1 574.351 N，矫正行程δ=2.653 mm,与实验结果F=1 574 N,δ=2.683 mm非常相近,误差非常小,验证了Y向变形矫正力数学模型的准确性.

2 超声振动矫形机构的设计与分析

2.1 振动矫形机构设计

拨叉弹塑性变形超声振动矫形机构如图6所示.该振动矫形机构主要包括驱动系统、传动机构、变形检测机构及振动矫形机构.其工作原理主要是利用外形检测机构采集拨叉的轮廓数据,并将数据输入计算机进行数据处理和分析,判断拨叉在加工过程中是否产生了变形;然后通过驱动系统控制传动机构带动振动矫形机构运动打拨叉相应的变形部位,对其进行矫正,实现整个机构的变形矫正功能.

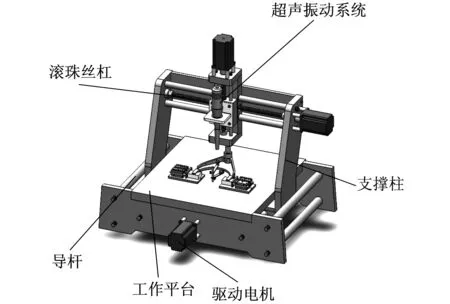
图6 检测矫形机构外形图Fig.6 Detection of outline of orthopaedic mechanism

2.2 关键零部件谐响应分析

谐响应分析的功能主要是检测零件整体结构的动力学特性,从而验证所设计的机构是否可以避免因共振或受迫振动而产生的不良效果[8-9].

变幅杆是超声振动矫形机构中关键的零部件,既要传递振动又要承受相应的矫正载荷,因此，必须对变幅杆进行谐响应分析,验证其动力学特性[10].变幅杆大端与换能器相连,前端与工具头相连,变幅杆整体较为薄弱的部位就是与工具头相连的端面.

变幅杆谐响应分析的步骤主要有:首先,在Solidworks中完成变幅杆三维模型的建立;然后,将其导入到Workbench中,设置材料,划分网格,施加相应的约束和载荷,借助“Harmonic Response”模块对变幅杆进行谐响应分析.变幅杆是通过自身的法兰盘进行固定的,因此,须对其法兰面施加固定约束,又因为矫形系统的最大载荷可能达到5 kN,所以给谐响应所赋予的激励载荷也为5 kN.

由于变幅杆的工作频率为20 kHz,因此，谐响应分析中的“Range Minimum”设置为19.5 kHz,“Range Maximum”的值设置为22.5 kHz,求解区间“Solution Intervals”为30,然后对变幅杆前端面的应力、变形和加速度进行了谐响应求解,具体的求解情况如图7所示[11].

图7 谐响应求解情况曲线图Fig.7 Curve diagram of harmonic response solution

由图7可以看出:应力频谱曲线出现了一个峰值,当响应频率为20.9 kHz时,变幅杆前端端面的应力达到了最大,且最大应力为2.43 MPa,相应的应力相位移降幅较大,从180°降到了0°;变形频谱曲线趋势与应力频谱曲线相同,也同样出现了一个峰值,在频率达到20.9 kHz时,变幅杆前端端面的位移达到了最大,且最大位移值为1.12 mm,相应的变形相位移降幅较大,从180°降到了0°;当响应频率为20.9 kHz时,加速度频谱曲线出现了一个峰值,变幅杆前端端面的加速度达到了最大,且最大加速度的值为1.94×1010mm/s2,加速度相位移与应力、变形相位移相反,从0°升到了180°.

综上所述,变幅杆应力频谱曲线的最大值为2.43 MPa,变形频谱曲线的最大值为1.12 mm,由设计结果可知，变幅杆的总长为136 mm,变形比例为0.82%,变形比例非常小,不会对变幅杆的性能产生影响.

变幅杆的工作频率为20 kHz,提取变幅杆在谐响应分析中频率为20 kHz时的应力及变形云图,如图8所示.变幅杆的最大应力为18.787 MPa,发生在截面左边,在材料安全限度以内;最大变形为4.11×10-3mm,发生在变幅杆前端端面处,且其余各处变形位移的分布完全符合振动规律.

图8 变幅杆应力及变形云图Fig.8 Stress and deformation nephogram of amplifier

3 矫形效果分析

本文完成了超声振动矫形机构的设计,如图9(a)所示.以叉脚弯曲变形为例,利用设计的振动矫形机构对其进行矫正试验,矫形效果如图9(b)所示.拨叉初始变形量的最大值为2.929 mm,矫形过后拨叉的残余变形仅为0.282 mm,矫形率达到了90.4%,验证了振动矫形方法的可靠性及有效性.

图9 振动矫形机构及矫形效果图Fig.9 Vibration orthopaedic mechanism andeffect chart

4 结论

(1) 利用弹塑性理论对拨叉的弹塑性变形进行了分析,得到了叉脚在X向和Y向的变形规律曲线,并针对不同的变形情况建立了相应的矫形数学模型,为振动矫形机构提供了一定指导作用.

(2) 利用振动理论，结合变形矫正模型设计了超声振动矫形机构,并对关键零部件变幅杆做了谐响应分析,验证了其设计的合理性和正确性.

(3) 利用设计的超声振动矫形机构对拨叉的塑性变形进行了矫形验证,结果表明,矫正率达到了90.4%,验证了超声振动矫形方法的有效性.