采用混合算法优化的液压驱动机械手PID控制仿真研究

王亚茹,王雪丽

(1.吉林工程职业学院 机电工程学院,吉林 四平 136001; 2.长春职业技术学院 工程技术分院,长春 130033)

随着工业自动化的发展,机械手装置在许多领域得到了广泛应用.机械手装置涉及机械、控制、传感器及人工智能等多种学科,是一种高技术自动化生产设备[1-2].由于液压驱动装置具有结构紧凑、运动平稳及位置精度高等优点,所以,液压驱动装置在机械手的发展中得到了迅速发展.液压机械手运动的外界环境因素多变,容易受到外界各种因素的影响.如果机械手控制系统设计不合理,就会使机械手运动轨迹产生偏差,有可能造成重大的经济损失.因此,研究机械手高精度控制系统,对于提高机械手市场的竞争力具有重要意义.

为了提高机械手控制系统抗外界干扰能力,需要设计出更好的控制系统.国内外学者对机械手控制系统展开了广泛研究.文献[3-4]研究了液压机械手PID控制系统,建立管柱移运液压机械手结构简图,设计液压缸PID控制系统框图,采用Matlab软件对PID控制系统进行仿真,获得良好的控制性能.文献[5-6]研究了液压伺服机械手控制系统,建立了机械手液压系统模型,给出了机械手液压伺服PLC控制方案,对末端执行器运动轨迹进行仿真验证,提高了机械手输出轨迹精度.文献[7-8]研究了机械手自适应滑模控制系统,建立机械手运动数学模型,设计了滑模控制系统,对控制系统的稳定性进行证明,通过仿真验证滑模控制效果,降低了机械手角速度跟踪误差.以前研究的机械手控制输出精度有所提高,但是,受到外界波形干扰时,其输出误差较大.对此,本文建立液压机械手平面运动简图,推导出阀控液压缸流量方程式,引用混合算法优化PID控制,给出PID控制优化流程图.采用数学软件Matlab对机械手优化后的控制进行仿真,输出机械手位移跟踪仿真曲线,并与常规PID控制系统仿真曲线进行对比,为提高机械手运动轨迹精度研究提供理论依据.

1 液压系统模型

本文研究的机械手采用液压驱动控制,其模型如图1所示.

图1 液压驱动机械手Fig.1 Hydraulic driving manipulator

在机械手中,液压驱动系统包括不对称气缸,其占据较小的工作空间,能够提供较高的有效载荷.气缸由伺服阀控制.位移传感器安装在活塞杆内部,形成位置闭环控制.阀控液压系统如图2所示.

图2 阀控液压缸示意图Fig.2 Drawing of valve-controlled hydraulic cylinder

假设电压是伺服阀的输入信号，并且阀动态可以用一阶传递函数表示,则阀芯位置和输入信号之间存在以下关系:

(1)

式中:xs为阀芯位置;us为输入电压信号;k为增益系数;s为输入指令信号.

阀控液压缸工作方程式为

式中:n=A1/A2;A1，A2分别为无杆腔和有杆腔面积;p1，p2分别为液压缸无杆腔和有杆腔压力;PL为负载压力;QL为负载流量;Q1，Q2分别为液压缸无杆腔和有杆流量.

阀门流量方程式[9]为

(4)

(5)

式中:cs为流量系数;ps，pt分别为泵和罐的压力.

活塞匀速运动进入液压缸流量方程式为

式中:x′为活塞的速度.

因此,可以推导出液压缸流量连续运动方程式为

式中:x为活塞的位移;V1，V2分别为气缸无杆腔和有杆腔体积;Be为体积弹性模量;Cic为液压缸泄漏系数;L为液压缸行程.

根据牛顿定律,活塞力的平衡方程式为

(10)

式中:b为活塞的黏性摩擦系数;m为有效载荷质量.

由式(3),(8)和式(9)可以得到

(11)

式中:Vt为液压缸体积;Ctc为总泄漏系数.

式(11)采用拉普拉斯变换后[9]为

(12)

2 PID控制器优化

2.1 PID控制

PID控制是工业控制系统中最常用的控制算法,其具有强大的性能并且易于实现.控制器由3个系数组成,即比例、积分和微分项,可以适当选择它们以获得最佳响应,如图3所示.

图3 PID控制流程Fig.3 PID control flow

PID控制微分方程式[10]为

(13)

式中:kp为比例系数;ki为积分系数;kd为微分系数.

PID控制器输出的误差方程式为

(14)

采用误差积分性能指标评价系统误差函数,当PID控制器设置参数最优时,误差函数取得最小值,可以提高系统输出精度.误差积分性能评价函数为

(15)

2.2 混合粒子群算法优化流程

粒子群算法由Kennedy和Eberhart等开发的一种新的进化算法[11].它从随机解开始,粒子通过搜索个体极值Pt和群体极值Gt,迭代更新自身速度V和位置X,迭代方程式[11]为

1938年8月，国民政府行政院举行第373次院会，会上通过了《沦陷区教育实施方案》，提出沦陷区的各级教育，应利用各种方法，继续维持教育，“以适应抗战需要，而延续文化生命”［22］291。在敌人已直接控制的沦陷区，督导员要“采用以抗战为中心之教材，秘密教导学生”，倘若这种教材难以获得，则由“学生辗转抄写或竟用口授”［22］292。对于尚未被敌人控制的区域，督导员要指导小学校长，在“尽可能范围内设法继续维持各该校正常教育”；对于已停闭的小学，“应尽量设法恢复”；各学校除授予正常课之外，还“应特别加授与抗战有关之教材”［22］293。

Vt+1=ωVt+c1r1(Pt-Xt)+c2r2(Gt-Xt)

(16)

Xt+1=Xt+Vt+1

(17)

式中:ω为惯性权重;c1,c2为速度更新参数;r1,r2为随机数.

为了充分发挥局部搜索和全局搜索各自优势,惯性权重系数修改为

(18)

式中:ω0为初始惯性权重系数;ω1为迭代最大次数惯性权重系数;t为当前迭代次数;T为最大迭代次数.

随着粒子迭代次数的增多,各个粒子就会出现相似情况,从而产生局部最优解.因此,在粒子群算法中混合遗传算法,对粒子实行交叉和变异操作,最终搜索到全局最优解.

交叉操作:采用实数交叉法对粒子群个体进行操作,第n个群体最优染色体An和第m个染色体Am进行交叉操作,其交叉方程式[12]为

变异操作:从种群中随机抽取一个个体,通过基因变异产生优秀个体,第i个个体第j个基因变异方程式[12]为

(21)

f(t)=1-r(1-t/T)a

(22)

式中:Amax为个体上界;Amin为个体下界;a为可调参数.

采用混合算法优化PID控制流程如图4所示.

3 仿真与分析

混合粒子群算法参数设置为:群体大小为100,惯性权重系数为ω0=0.9,ω1=0.4,速度更新参数

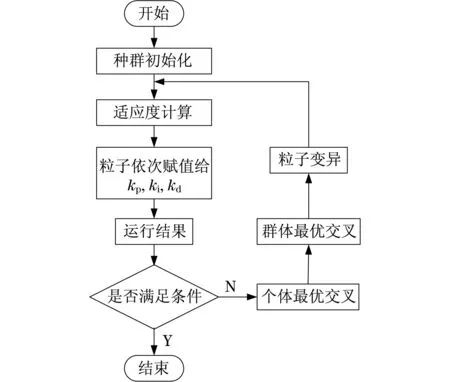
图4 混合粒子群算法优化流程Fig.4 Hybrid particle swarm optimization

c1=c2=2,变异概率为0.6,交叉概率为0.01.采用Matlab软件优化后的PID控制系统进行仿真,仿真参数如表1所示.

表1 PID控制系统仿真参数Tab.1 Simulation parameters of PID control system

分别采用阶跃波形和正弦形，对优化后的液压机械手PID控制系统跟踪效果进行仿真验证,并与优化前的PID控制效果进行对比.假设外界环境没有波形干扰,其仿真结果分别如图5和图6所示.假设外界环境有正弦波形干扰(y=2sin πt),其仿真结果分别如图7和图8所示.

由图5和图6可知：在没有干扰环境条件下,液压驱动机械手运动位移为阶跃波和正弦波信号时,采用PID控制和混合粒子群算法优化PID控制都能快速地实现位移跟踪.由图7和图8可知：在有正弦波干扰环境条件下,液压驱动机械手运动位移为阶跃波和正弦波信号时,采用PID控制,信号跟踪反应时间较长,机械手跟踪误差较大.采用混合算法优化PID控制,信号跟踪反应时间较短,机械手跟踪误差较小.在相同外界环境条件下,采用混合算法优化PID控制,不仅反应速度快,而且输出精度高.因此,采用混合粒子群算法优化PID控制,能够改善液压驱动机械手控制性能指标,提高机械手运动轨迹的跟踪精度.

图5 阶跃波形位移跟踪(无波形干扰)Fig.5 Step waveform displacement tracking(no waveform interference)

图6 正弦波形位移跟踪(无波形干扰)Fig.6 Sinusoidal waveform displacement tracking(no waveform interference)

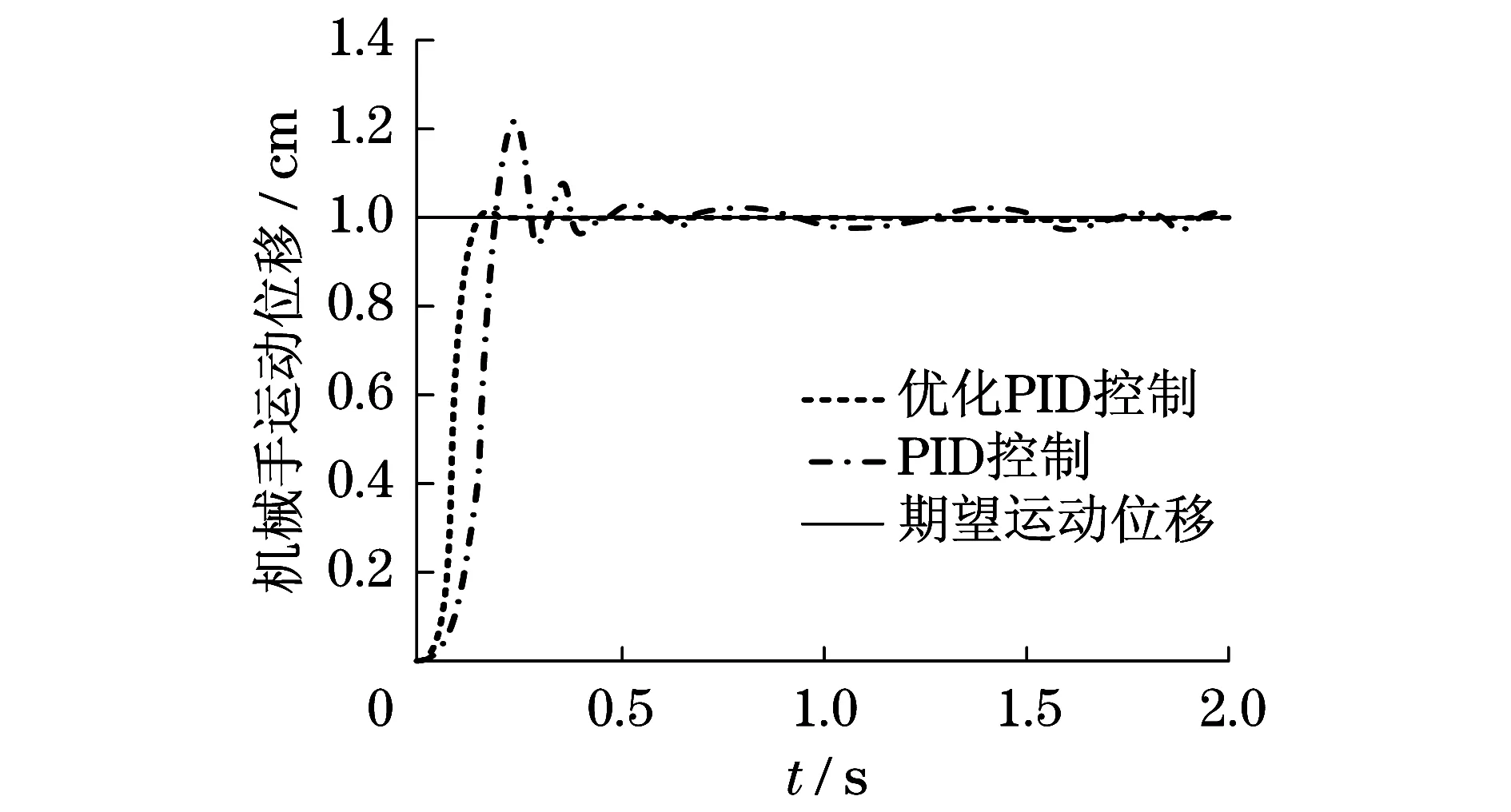
图7 阶跃波形位移跟踪(有波形干扰)Fig.7 Step waveform displacement tracking(with waveform interference)

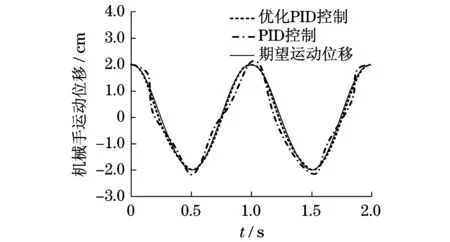
图8 正弦波形位移跟踪(有波形干扰)Fig.8 Sinusoidal waveform displacement tracking(with waveform interference)

4 结论

本文采用混合粒子群算法优化液压驱动PID控制,并对优化后的控制系统反应速度和跟踪误差进行仿真验证,主要结论如下:① 混合粒子群算法增加了遗传算法的交叉和变异操作,能够避免产生局部最优解,适合PID控制参数优化；② 液压驱动机械手采用混合粒子群算法优化PID控制系统,能够抑制外界环境因素的干扰,反应速度快,输出精度高.