超起装置对起重机伸缩臂的稳定性影响
佘占蛟,姚峰林,孟文俊,石国善,白艳强
(1.南充职业技术学院 机电工程系,四川 南充 637131; 2.太原科技大学 机械工程学院,太原 030024)
随着客户对全地面起重机的起重量和起升高度的要求提高,伸缩臂的全伸长度越来越长,因此,保证伸缩臂的稳定性成了发展大型全地面起重机必须解决的问题之一.为了解决大型全地面起重机伸缩臂的稳定性问题,大部分厂家都选择了在臂架上加装超起装置.由于我国全地面起重机起步相对较晚,加之受到国外技术封锁,导致我国全地面起重机与西方发达国家仍有一定差距,特别是5节以上伸缩臂及其超起装置的设计在《起重机设计规范》中暂无相应规范,在此方面的理论尚不成熟,需要进一步深入研究[1].伸缩臂的稳定性主要研究内容是确定其失稳形态和屈曲临界载荷[2].近年来,国内外行业专家对伸缩臂、细长杆等的稳定性给予了足够的重视,并取得了丰硕成果[3-6].本文对带超起装置的伸缩臂系统进行了简化,发现超起撑杆高度、超起撑杆夹角以及超起撑杆的铰接位置都将对伸缩臂的稳定性产生影响,采用有限单元法对超起装置的几何参数对伸缩臂屈曲临界吊载的影响规律进行了研究.
1 对含超起装置的伸缩臂简化
目前我国《起重机设计规范》中对于5节(含5节)以下不带超起装置的伸缩臂临界载荷的计算已经比较成熟.为了降低对带超起装置伸缩臂稳定性的探讨难度,可先将带超起装置的伸缩臂系统简化为不含超起装置的伸缩臂.带超起装置的伸缩臂系统如图1所示.

图1 带超起装置的伸缩臂系统Fig.1 Telescopic boom with super-lift system
假如图1中带超起装置的伸缩臂处于平衡状态,两侧超起拉索均处于理想对称作用.几何参数如下:超起撑杆高度CD=CM=H;超起撑杆夹角∠MCD=φ=2θ;F2为单侧超起拉索拉力;F3为单侧超起拉板拉力;F1为单侧超起撑杆压力;记AC=L,CE=L1,ξ=L1/L.
将带超起系统的伸缩臂进行简化后,可得到简化后的伸缩臂,如图2所示.将简化后的带超起装置的伸缩臂与不含超起装置的伸缩臂进行对比,不难发现多出了F4,F5,M,
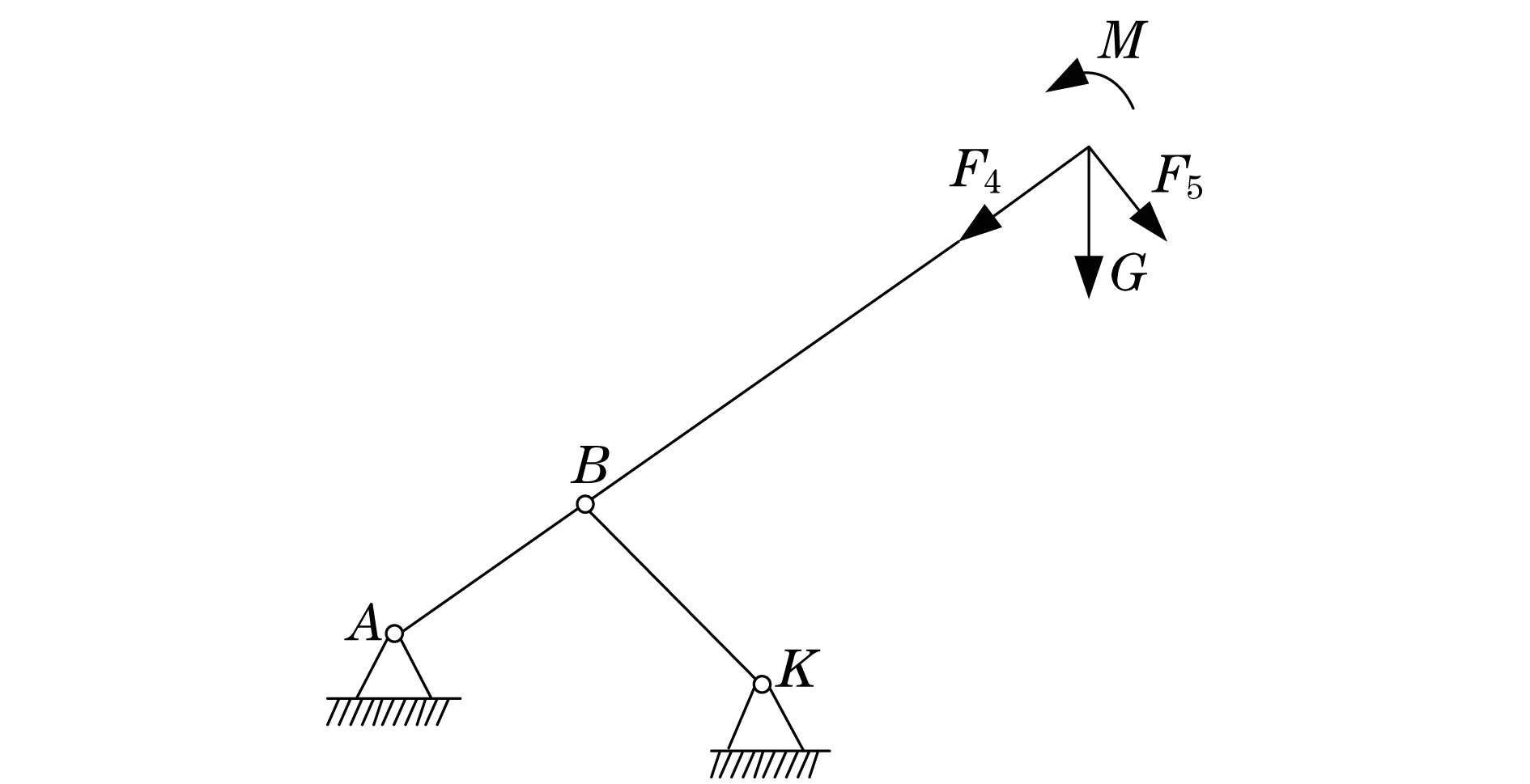
图2 简化后的伸缩臂Fig.2 Simplified telescopic boom
从式(1)~式(3)可以看出,简化后的力F4,F5以及弯矩M几乎都含有H,F2,L1,ξ,θ,所以,超起撑杆高度、超起撑杆夹角以及超起撑杆的铰接位置都将对伸缩臂的稳定性产生影响.
2 屈曲分析理论
屈曲分析包括线性屈曲分析和非线性屈曲分析,主要用于确定结构失稳的临界载荷.线性屈曲分析是基于线弹性理想结构的假设而进行的分析,其结果与Euler方程求得的基本一致.
当结构发生屈曲时,其临界载荷可表示为
(4)
式中:λ0为屈曲特征值或载荷因子;P0为屈曲时加载的初始载荷.
从式(4)不难看出,采用线性屈曲计算临界载荷关键是计算特征值(载荷因子)λ0.
线性屈曲分析计算特征值λ0的一般方程为
(5)
式中:[K]为结构总体弹性刚度矩阵;[S]为结构总体几何刚度矩阵;λ0j为模态对应的屈曲特征值(载荷因子);{ψj}为屈曲模态;j为屈曲模态阶数,模态阶数选取为1.
线性屈曲未考虑结构缺陷以及非线性,算出的屈曲临界载荷为上限值,但在计算效率方面远远优于非线性屈曲分析,且为非线性屈曲分析加载提供参考,所以线性屈曲仍被广泛采用[7].本文采用线性屈曲分析方法研究超起装置几何参数对伸缩臂屈曲临界吊载的影响规律.
3 有限元分析过程
本文以某厂300 t全地面起重机伸缩臂为实例,分别对其2节臂、3节臂、4节臂、5节臂工作时,超起装置各几何参数对伸缩臂的临界吊载影响进行分析.
在进行有限元模型建立前需对模型所采用的单元以及材料属性等进行定义,本文中主臂采用SHELL181单元,超起撑杆采用BEAM188单元,超起拉板、超起拉索采用LINK180单元.ANSYS 15.0中不能对BEAM188单元和SHELL181单元定义实常数,需在Sections中分别给BEAM188定义截面,赋予SHELL181伸缩臂上下盖板厚度.LINK180可以定义实常数,由于文中超起拉板和超起拉索的截面积不同,因而需要定义两个实常数.本文中主臂和超起装置所采用材料属性如表1所示.

表1 超起装置及伸缩臂材料属性Tab.1 Super-lift system and telescopic boommaterial properties
3.1 模型建立
定义好所需单元、实常数、材料以及截面Sections后,便可进行有限元模型建立,本文中伸缩主臂为U型截面.本文采用APDL命令流进行建模,运用自下而上的建模方式[8].模型建好后,为简化计算可直接将臂节之间放置滑块位置处通过节点耦合连接起来,超起撑杆与主臂之间通过MPC接触对连接起来,超起拉索和超起拉板直接通过主臂、撑杆上的两节点生成LINK180单元.建立好的含超起装置伸缩臂有限元模型如图3所示.

图3 有限元模型Fig.3 Finite element model
3.2 网格划分
划分主臂网格时,采用AATT命令流先赋予单元属性(包括材料号、单元号、单元截面号),再运用ESIZE命令流控制网格划分精度、MSHKEY选择网格划分方式,最后运用AMESH命令流选择即将划分的主臂面.同样,划分超起撑杆时,采用LATT命令流先赋予单元属性,再用LESIZE命令流控制网格划分精度,最后用LMESH命令流进行超起撑杆的网格划分.
3.3 添加约束及载荷
为了模拟符合实际情况,将基本臂与转台的铰接点和变幅油缸与基本臂的铰接点处,沿x,y,z3个方向的平移自由度和绕y,z转动自由度约束,释放绕x轴转动自动度.
伸缩臂所受载荷众多,其中包括自重载荷、起升载荷、起升绳拉力、物品偏摆产生的水平力,以及风载荷等,其计算公式如下.
自重载荷:可通过给模型添加重力加速度g来考虑重力载荷.
起升载荷PQ为
(6)
式中:φ2为起升动载系数;mQ为有效起质量;m0为吊具自重.
起升绳拉力FS为
(7)
式中:n为倍率;η为起升滑轮组效率.
物品偏摆产生的水平力FT为
(8)
式中:α为允许的物品偏摆角,α为6°.
风载荷PW为
(9)
式中:C为风力系数;PΠ为工作状态计算风压;A为伸缩臂侧向的实体迎风面积.

将上述伸缩臂所受载荷分别加在臂端相应方向上,如图4所示.

图4 添加约束和载荷Fig.4 Add constraints and loads
4 超起装置几何参数对伸缩臂临界吊载的影响
4.1 超起撑杆夹角φ的影响
采用有限单元法分析超起撑杆夹角φ对伸缩臂临界吊载的影响,即选取的工况如表2所示.为了不影响伸缩臂正常伸缩,一般都将超起撑杆铰接在基本臂上,令超起撑杆铰接点至基本臂起点的距离与基本臂的长度之比为μ.
将表2中4种工况下,临界吊载随超起撑杆夹角φ的变化计算出来,可得到图5.
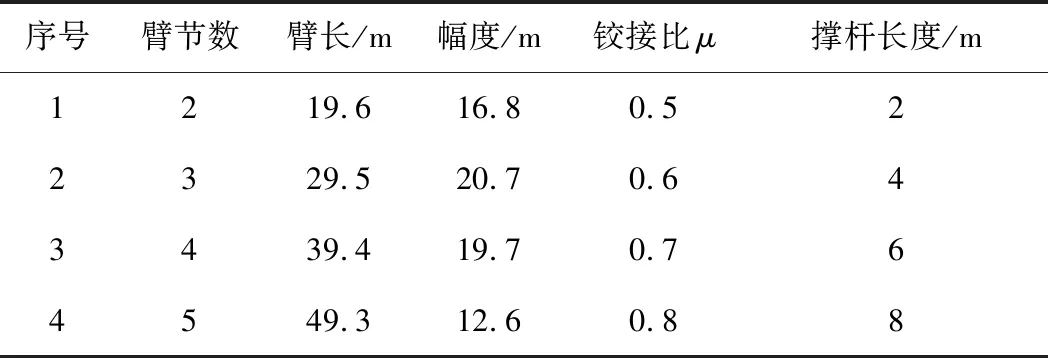
表2 工况Tab.2 Working conditions

图5 φ对伸缩臂临界吊载影响曲线Fig.5 Influence of φ on critical lifting load of telescopic boom
4.2 超起撑杆长度H的影响
采用有限单元法分析超起撑杆长度H对伸缩臂临界吊载的影响,即选取的工况如表3所示.
将表3中4种工况下,临界吊载随超起撑杆长度H的变化计算出来,可得到图6.
4.3 超起铰接位置的影响
采用有限单元法分析超起装置铰接位置对伸缩臂临界吊载的影响,即选取的工况如表4所示.

表3 工况Tab.3 Working conditions

图6 H对伸缩臂临界吊载影响曲线Fig.6 Influence of H on critical lifting load of telescopic boom
将表4中4种工况下,临界吊载随超起装置铰接比μ的变化计算出来,可得到图7.
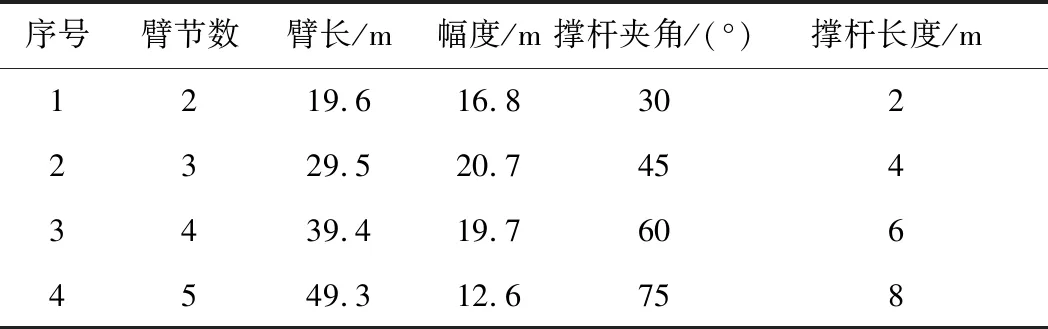
表4 工况Tab.4 Working conditions

图7 μ对伸缩臂临界吊载影响曲线Fig.7 The Influence of μ on the critical liftingload of telescopic boom
5 结论
本文先对带超起装置的伸缩臂系统进行了简化,结果发现超起撑杆高度、超起撑杆夹角以及超起撑杆的铰接位置都将对伸缩臂的稳定性产生影响;然后采用有限单元法,对某起重机厂300 t全地面起重机的超起装置几何参数对伸缩臂的屈曲临界吊载的影响进行了研究.通过研究发现:
(1) 临界吊载先随着超起撑杆夹角φ增大而增大,当夹角φ超过一定角度时,临界吊载将随着超起撑杆夹角φ增大而减小.
(2) 临界吊载随着超起撑杆长度H的增大迅速增大,当超起撑杆长度H达到某一长度时继续增大H值,由于超起撑杆截面不变致使自身刚度不够,将使得临界吊载下降.
(3) 临界吊载随着超起装置在基本臂上的铰接比μ增大而增大,说明将超起撑杆安装在基本臂靠近末端最有利.

