飞机液压管路支撑的2自由度动力学模型研究
权凌霄,赵文俊,付旭鹏
(1.燕山大学 机械工程学院,河北 秦皇岛066004;2.燕山大学 河北省重型机械流体动力传输与控制实验室,河北 秦皇岛066004;3.江苏恒立液压科技有限公司,江苏 常州213000)
液压管路作为飞机液压传动系统的重要组成部分,是飞机安全飞行的重要保障。在柱塞泵或发动机工作以及气流扰动、着陆撞击、特殊机动等复杂环境产生的简谐振动和随机振动作用下,振动激励经过支撑结构传递至管路系统;振动激励长久循环作用时,将引发管路磨碰或疲劳损伤以及支撑松动;当管路的固有频率与基础振动频率相接近还会引发谐振[1–2]。飞机液压传动系统中,液压管路通过若干数量的管路支架和卡箍约束到机体结构上,从而实现管路的支撑和固定。管路支架和卡箍通常以组合形式构成一个支撑组件,其中,卡箍用以约束管路、释放应力及吸收振动和冲击[3];支架起到支撑和稳固管路的作用。飞机液压传动系统具有分布广、线路长、空间结构多变及工作环境复杂等特点。除了要抑制振动能量在管路结构中传递以外,管路和机体间的隔振特性也是管路系统减振降噪的重要研究内容之一。
飞机液压管路系统的机械振动控制通常采用改变管路构形或支撑参数来控制管路振动的幅值、频率或相位,以达到避开激振源的共振频率和减小振幅的目的[4–5]。然而,由于空间限制,相比管路空间构形优化,通过调整支撑参数来改变管路系统的振动特性是一种有效且常见的方法[6–7]。
从隔振角度出发,卡箍和管路支架可被看作是隔振器,对管路振动的抑制起到积极作用,是管路振动的有效被动控制方式。因此,进行卡箍及管路支架的动力学特性分析对了解其动态特性以及对减小管路系统振动、提高系统工作性能及其可靠性具有重要意义。
本文针对“机体结构-支撑组件-液压管路”机械振动系统中的管路支架和卡箍,采用ABAQUS软件建立有限元模型,分别在指定频段范围内进行谐响应分析,获取动刚度及加速度导纳特性。在此基础上,基于经典隔振理论,将机体结构视为弹性体,考虑支撑组件质量、阻尼及刚度,建立以机体结构为振动激励源、液压管路为振动受体的管路支撑组件2自由度物理模型,采用四端参数法推导支撑组件的位移/力传递率,对位移传递率的影响因素进行分析,为飞机液压管路支撑组件的参数优化提供参考。
1 隔振性能参数指标及分析
管路支架和卡箍作为飞机液压管路上使用的隔振结构,其性能参数主要包括外形尺寸、重量、刚度/阻尼系数、振动导纳和阻抗等。由于受数值分析方法和有限元软件力学分析的条件限制而无法同时考虑多维耦合振动环境下的振动传递特性,依据参考文献[8]将P卡与管路支架的三向刚度特性单独进行有限元分析。此外,设计阶段常用的评价指标还有传递率[9]。
在飞机机体带来的动态载荷作用下,管路支撑的动刚度是指管路支架或卡箍抵抗变形的能力,其倒数为位移导纳或动柔度。在NVH(Noise、Vibration and Harshness)研究领域得到广泛应用[10]。当管路支架的动刚度不足时,会对管路的振动特性和疲劳寿命产生不良影响。振动传递率是评价和描述隔振元件的隔振效果的常用指标之一[11]。由于元件的隔振作用,基础结构的振动信号经过隔振元件并传向振动受体传递时信号特性将发生改变。飞机飞行工况下,吊挂区域振动激励通常为航发转子动不平衡产生的周期性振动,其可简化为简谐振动,其中f=Fejwt。由于管路布置受空间限制,位移传递率更加引人关注,当传递率小于1 时,认为隔振有效,且传递率越小说明通过隔振元件传递的振动越小,隔振效果也越好。
1.1 管路支架的动态特性分析
常见的管路支架结构形式为L 型和Z 型,以ARJ21-700 支线客机吊挂区域的某Z 型管路支架为分析对象,研究其隔振性能。
(1)静刚度
Z 型管路支架底部螺栓孔为固定约束,在顶部卡箍连接孔上施加沿y向的静载荷F,其等效大小为10 N,图1 为支架在载荷F 作用下的静态位移云图,顶部卡箍连接孔的相对平均变形量约为17.6 mm。
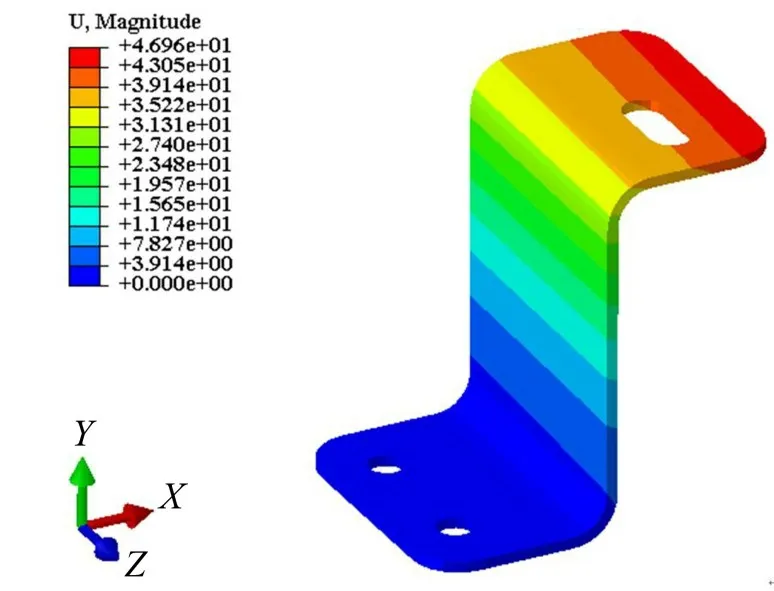
图1 支架Y向静态位移云图
计算可得管路支架在y 向的静刚度系数ky=5.68×102N/m,同理,x 向和z 向的静刚度系数kx和kz分别为1.21×102N/m和1.44×103N/m。
(2)动刚度及加速度导纳
对管路支架有限元模型进行模态频响求解,求解频率范围为0~2 000 Hz;顶部卡箍连接孔施加幅值为10 N沿y向的集中力,以激励点作为响应点,计算原点加速度导纳和动刚度,如图2和图3所示。
从分析结果看,管路支架的基频和主频分别为110 Hz 和165 Hz;在强迫激励作用下,管路支架在165 Hz、545 Hz 和1 590 Hz 频率附近产生较大加速度峰值;管路支架的动刚度随激励频率增大而波动性增大,其波动峰值与管路支架发生谐振有关,激励频率为零时,管路支架的动刚度约等值于静刚度值。
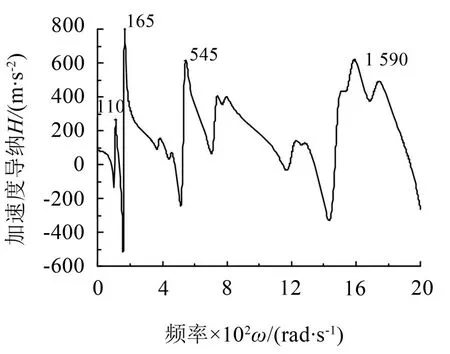
图2 支架原点加速度导纳

图3 支架原点动刚度
1.2 卡箍的动态特性分析
P卡由不锈钢环形基体和橡胶外衬2部分组成;块卡则由2个分体橡胶块和2个金属压紧垫片组成。以ARJ21-700 支线客机吊挂区域的P 卡为分析对象,研究其动力学性能。
(1)静刚度
建立P卡的有限元简化模型。其中,P卡底部螺钉孔处设置为固定约束,其与管壁接触面上施加沿y向的静载荷,等效大小为1 000 N,图4为P卡在等效静载F 作用下的静态位移云图,其与管壁接触面的相对平均变形量约为7.54 mm。
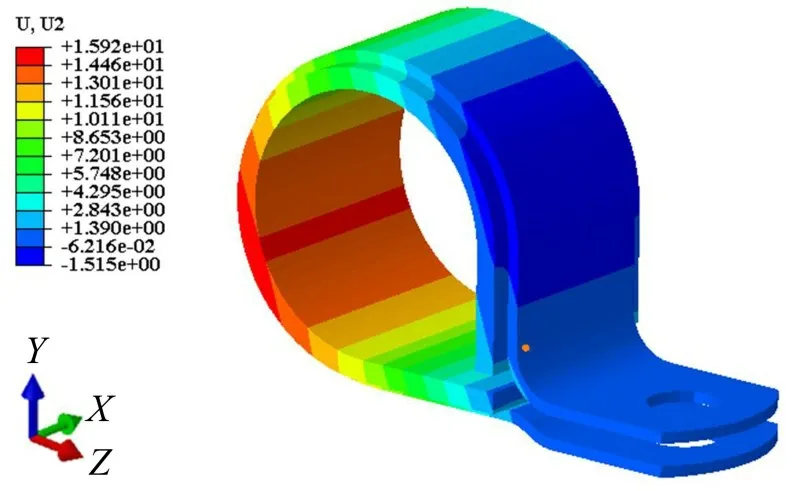
图4 P卡Y向静态位移云图
计算得到P 卡在y 向的静刚度系数ky=1.32×105N/m,同理得到x 向和z 向的静刚度系数kx和kz分别为1.02×106N/m和2.03×105N/m。
(2)动刚度及加速度导纳
对其有限元模型进行模态频响求解,求解频率范围为0~2 000 Hz,P 卡与管壁接触面上施加沿y向的幅值为1 000 N 的集中力,以激励点作为响应点,计算原点加速度导纳和动刚度,如图5 和图6所示。

图5 P卡原点加速度导纳
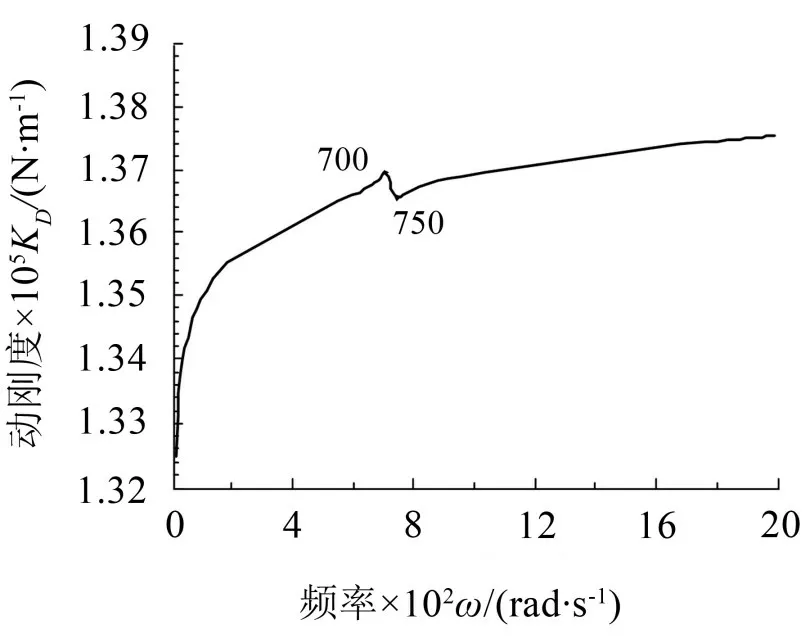
图6 P卡原点动刚度
从分析结果看出,在0~700 Hz 频段,P 卡的动刚度逐渐增加,抵抗动载能力增强,相应地,其加速度导纳逐渐减小;同样地,在750 Hz~2 000 Hz 频段,动刚度和加速度导纳曲线变化趋势亦相反。在720 Hz激励频率附近原点加速度响应出现了共振峰与反共振峰,其与动刚度曲线的波动频率一致。
2 管路支撑组件的隔振分析
2.1 管路支撑组件2自由度隔振模型建立
以ARJ21-700支线客机吊挂区域中使用的管路支撑组件进行分析,结构如图7所示,其通常在布置单根或双根导管情况下被使用,使用螺钉和自锁螺母将其固定在与机体相连的结构上。
根据经典隔振理论研究其隔振性能,建立支撑组件的力学模型。经典隔振理论模型通常是将基础结构视为无限刚度、隔振器视为无质量的弹簧和阻尼器、被隔振对象视为理想质量块的单自由度隔振系统[12]。

图7 管路支撑组件示意图
以往的管路系统振动特性分析中,通常采用单自由度、无质量的弹簧-阻尼系统来模拟支撑组件,这样的简化方式在一定程度上满足了工程分析的要求。但忽视了支撑组件本身质量的影响,而支撑组件的固有特性对管路系统的振动响应会产生一定的影响。同时,基础结构通常是机体内的腹板或肋板等结构,其并非是理想刚体,而具有一定的弹性[13]。因此,本文在建立管路支撑组件的力学模型时,将支撑组件简化为2自由度隔振系统,如图8所示。

图8 管路支撑组件简化模型
在不考虑管路弯曲振动情况下,将管段长为L的液压管路简化为集中质量m2,考虑支撑组件的本身质量m1,P 卡与管路的连接刚度和阻尼视为k2和c2,管路支架与机体肋板或腹板的连接刚度视为k1和c1,Fi和Xi分别表示系统各单元的广义力和广义位移。由于在实际安装环境中,飞机液压管路支架通常固定在具有一定弹性的基础结构上。此时基础结构的位移X1不再为零。
2.2 管路支撑组件力及位移传递率数值求解
采用四端参数法推导图8所示的管路支撑组件隔振模型的位移传递率和力传递率;图9(a)和图9(b)所示分别为该隔振模型的四端参数线路图及其简化形式,图中的箭头指向为能流的传递方向。
上一个单元的输出为下一个单元的输入时,这两个单元形成了一个串联单元;当多个单元以串联的联结形式构成一个组合单元时,整个组合单元的四端参数矩阵即等于各个子单元的四端参数矩阵的乘积;结合传递简化图可以推得组合单元的四端参数方程为
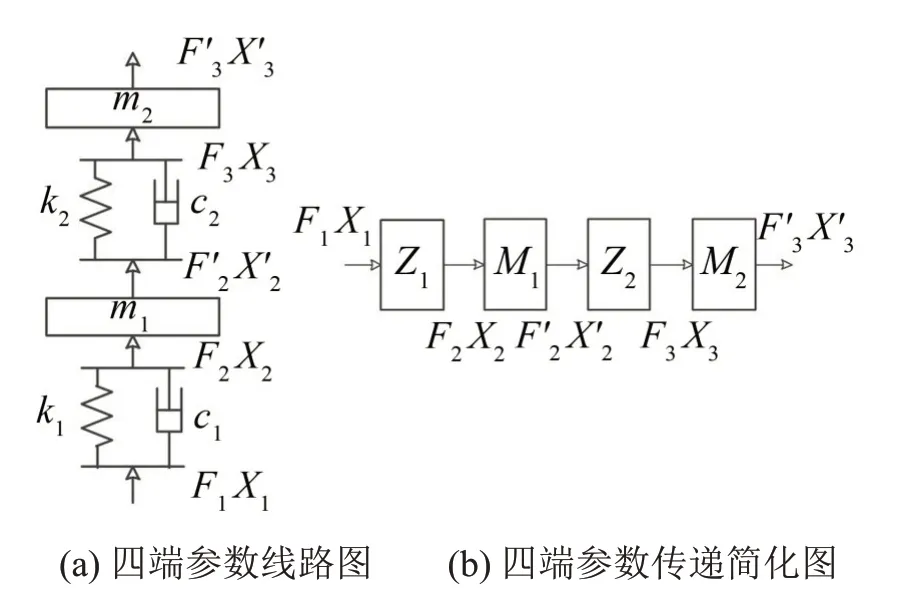
图9 四端参数传递简化图
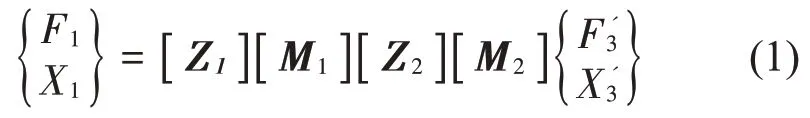
式中:[Zi]为刚度与阻尼并联单元四端参数矩阵;
[Mi]为质量单元的四端参数矩阵。
分别计算质量单元以及弹簧与阻尼并联的组合单元的四端参数矩阵。图10 为质量单元的受力状态。
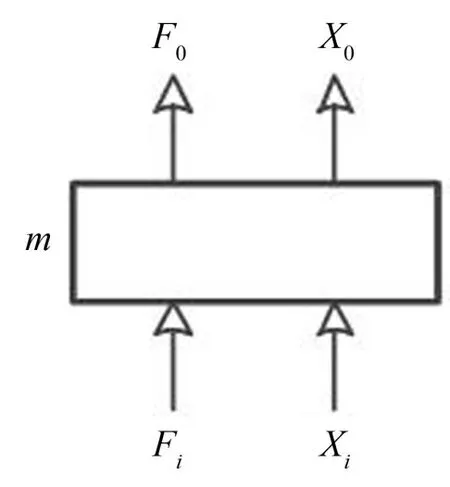
图10 质量单元受力图
对其纵向运动进行分析,假设其为刚度无限大的质量单元,则Xi=Xo;依据牛顿第二定律,即Fi-联立两式即得矩阵方程为
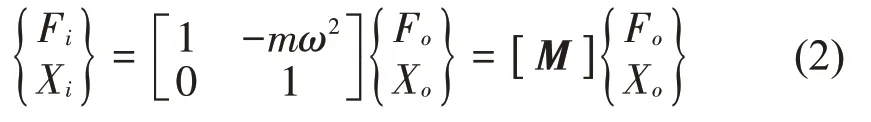
图11 为弹簧单元的受力状态,分析其纵向运动。
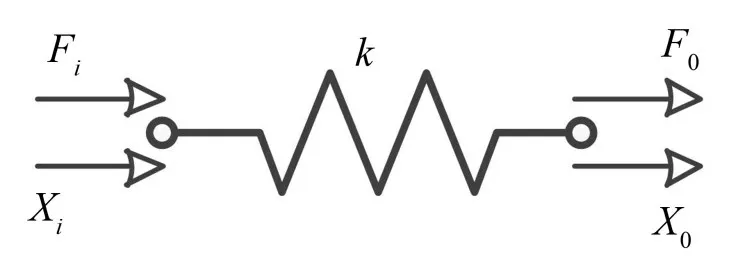
图11 弹簧单元受力图
忽略弹簧单元质量,有Fi=Fo=k(Xi-Xo),可得其矩阵方程为
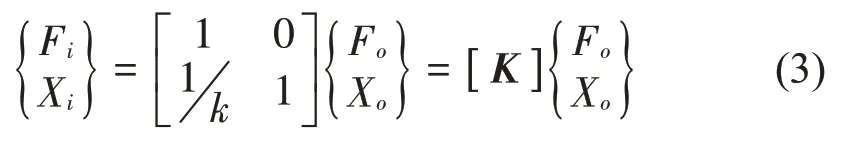
图12为阻尼单元的受力状态,分析其纵向运动。
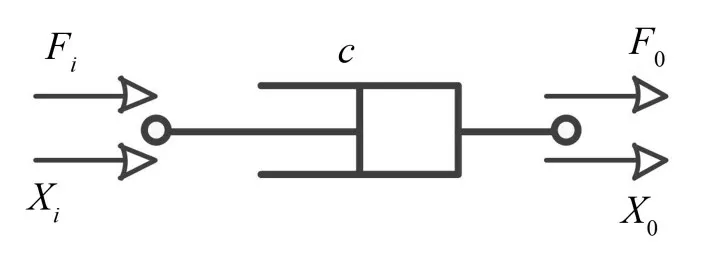
图12 阻尼单元受力图
同理可得其矩阵方程为
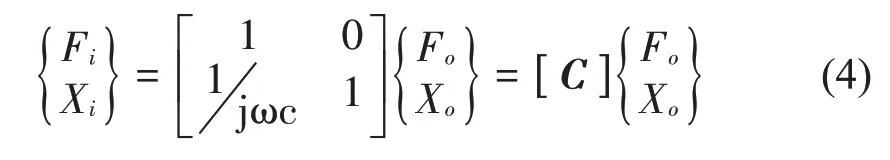
综上,由振动理论,得到弹簧和阻尼并联组合单元的矩阵方程为

如图9 所示,由于质量单元m2上表面无任何外界约束,即其输出端为自由时,外界作用力F'3=0。将式(2)和式(5)代入式(1)可得管路支撑隔振系统的传递方程为

已知F3=-m2ω2X3,代入式(7)得到

可以看出,位移传递率和力传递率不仅与k、c和w 有关,而且还与管路段L 的质量m2及支撑组件质量m1有关。当不考虑结构阻尼时,得到位移传递率μX和力传递率μF为

为形象地描述管路支撑组件的隔振效果,依据参考文献[14],设直径约为19 mm、壁厚约为0.991 mm的不锈钢液压管路在严酷环境下的支撑间距为400 mm,其材料弹性模量为1.96×1011Pa,密度为7.76×103kg/m3,泊松比为0.27;P卡与管路的连接刚度k2为1.32×105N/m,管路支架与机体肋板或腹板的连接刚度k1为5.68×102N/m;通过计算得到管段长400 mm的液压管路简化为集中质量m2为0.174 kg,支撑组件本身质量m1为2.59×10-2kg。根据式(9)编写MATLAB求解程序,得到支撑组件的位移传递率曲线如图13所示。

图13 位移传递率曲线
(1)管路支架与机体的连接刚度对支撑组件隔振系统位移传递率的影响。
通过有限元分析得到了管路支架的垂向刚度k1=5.68×102N/m,为此,同样选用垂向刚度分别为5.68×103N/m 和5.68×104N/m 的管路支架进行对比分析,得到位移传递率μX曲线如图14所示。
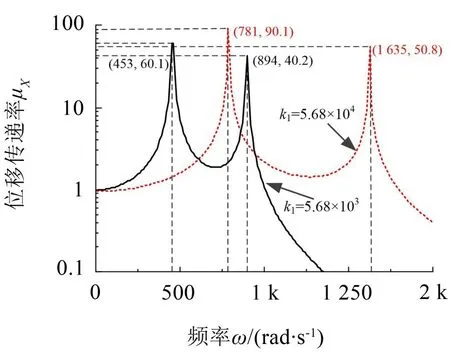
图14 管路支架刚度k1对位移传递率的影响
对比图13和图14中曲线可以看出,管路支架刚度对位移传递率有显著影响,刚度小时的曲线峰值要小于刚度大时的曲线峰值,且峰值频率前移,衰减较快;因而可知,管路支架刚度k1是影响支撑组件隔振效果的一个重要因素,但并非k1越小时隔振效果越好,在低频区,k1越小反而不利于支撑组件的隔振。
(2)P卡与管路间的连接刚度对支撑组件隔振系统位移传递率的影响。
通过有限元分析得到了P 卡的垂向刚度k2=1.32×105N/m,为对比P卡刚度对支撑组件隔振性能的影响,分别选用为1.32×106N/m 和1.32×107N/m两个刚度进行计算,得到位移传递率μX曲线如图15所示。

图15 P卡刚度k2对位移传递率的影响
对比图13和图15可以看出,P卡刚度是影响支撑组件隔振性能的一个重要因素;当P 卡的刚度增大时,支撑组件的位移传递率曲线在1 阶峰值处无明显变化,然而其2阶峰值对应的频率后移,同时位移传递率衰减较快。可见k2对激励频率小于250 Hz时的隔振性能无显著作用,随着刚度值k2或激励频率的增加,隔振性能越加明显。
(3)支撑组件的集中质量对隔振系统的位移传递率的影响。
通过有限元计算得到支撑组件的质量m1约为2.59×10-2kg,为对比支撑组件集中质量对支撑组件隔振性能的影响,分别再选取集中质量为3.89×10-2kg和5.18×10-2kg两组数据进行解析,得到位移传递率μX曲线如图17所示。

图16 支撑组件质量m1对位移传递率的影响
通过对比图13和图16的曲线可以看出,支撑组件的质量对位移传递率2阶峰值的对应频率无明显影响;然而,随着支撑组件质量的减小,位移传递率曲线的1阶峰值和2阶峰值均有所降低,其中一阶峰值衰减更为明显。
可知,支撑组件的质量m1及P 卡与管路间的连接刚度k2减小时,能够降低支撑组件的位移传递率,有利于改善隔振效果;管路支架与机体的连接刚度k1减小时,位移传递率曲线的峰值频率前移,但是在1 000 Hz 后迅速衰减,因此在高频段具有更好的隔振效果。
(4)结构阻尼对隔振系统的位移传递率的影响。
考虑结构阻尼参数时,依据参考文献[15]将P卡和管路支架的材料耗散特性作为集中参数;令P 卡的阻尼系数c1为0.1,管路支架的结构阻尼系数c2为0.04。分别计算有无阻尼时的位移传递率μX曲线如图17所示。

图17 结构阻尼对位移传递率的影响
对比图17中的两条曲线可以看出,支撑组件的阻尼参数有利于减小位移传递率曲线的各阶峰值,但峰值衰减效果并不明显。
3 结语
针对飞机液压管路支撑组件进行了隔振特性分析。从隔振的角度,首先介绍了评价和描述隔振性能的常用指标,通过ABAQUS软件分别对管路支架和卡箍进行动态特性分析,得到了原点动刚度和加速度导纳;建立了管路支撑组件的2 自由度物理模型,采用四端参数法推导并求解了管路支撑组件的位移/力传递率,对位移传递率的影响因素进行分析,得以下结论:
(1)随激振频率的递增,管路支架和卡箍的动刚度值均呈上升趋势,受共振现象的影响,在固有频率附近处出现幅值波动。
(2)影响支撑组件隔振性能的主要因素是刚度参数k1和k2,其不仅影响位移传递率曲线的幅值,同时导致峰值产生频移。支撑组件的质量参数和结构阻尼参数主要对曲线幅值产生不同程度的影响。
(3)在飞机支撑组件实际设计安装时,根据各机身区域载荷频段的差异,合理调整组件各刚度参数以避开共振频率;同时,对于轻量化的飞机管路系统而言,支撑组件的质量对其位移传递具有一定影响,工程设计时可对支撑组件质量参数值进行寻优设计。

