双底面电力电容器底部空气层尺寸设计方法
李德玺,匡 兵,刘夫云,王娇娇, 姚春革
(1.桂林电子科技大学 机电工程学院,广西 桂林541004;2.桂林电子科技大学 信息科技学院,广西 桂林541004)
在高压、大容量直流输电过程中,换流站中的变压器、平波电抗器、滤波电容器等装置所辐射出来的噪声已经超出相关部门所拟定的场界标准[1–3]。其中,滤波电容器是换流站噪声的主要来源之一。
换流站设备由于产生大量的高次谐波,并且台数目较多,使得电容器等装置产生的噪声对周边居民正常的生活产生诸多不利的影响,滤波电容器所产生的噪声是高压、特高压直流输电工程中一个不可忽视的问题。因此,国内外学者对电容器振动与噪声进行多项研究[4–5],其研究结果对于治理电容器噪声有着重要的学术价值和工程意义。例如,祝令瑜[6]等人通过对电力电容器进行振动噪声测试,并对电容器外壳的6个表面的辐射噪声贡献量进行定量分析,结果显示:电容器底面振动是其外壳辐射噪声产生的主要来源之一。因此,有效降低电容器底面噪声对于治理电容器噪声至关重要。
现阶段电容器底部降噪方法主要是在底部增加一个内部为空气层的双底面结构,此结构加工成本低,降噪效果明显。吴鹏[7]等设计了双底面型低噪声电容器,将腔体焊接到电容器底部,中间为密封的空气介质。实验结果表明:与普通电容器相比其底部噪声水平降低了8 dB~15 dB。左强林等[8]尝试了多种电容器降噪措施并进行对比,试验结果证明目前较为有效的电容器底面降噪方法是在电容器底部增加双底面空腔结构。
目前对于电容器底部双底面结构的空气层尺寸参数的确定主要是通过大量振动噪声试验来确定的,工程成本较高,并未针对此结构进行设计、计算。因此本文针对单台电力电容器底部噪声问题,提出一种针对电容器主要噪声频率的双底面电容器空气层尺寸的设计方法,并设计试验方案验证此方法的准确性。
1 电容器振动噪声机理分析
1.1 电容器结构分析
电容器主要是由下列几部分组成:芯子、壳体、电介质引线铁、绝缘瓷套管[9]。电容器芯子以芯子单元为基本单元,由两块缠绕的铝箔片和一定长度的聚丙烯薄膜缠绕而成。在电容器的壳体内充满绝缘油体,壳体保持密封状态。
电容器辐射噪声主要是由壳体内部芯子元件振动引起,分析壳体内部芯子元件振动可知:当电容器中加载有基波电压和谐波电压激励时,电容器两极板间产生电场力,引起电容器芯子的受迫振动,并通过绝缘油或固定支撑件传递至电容器外壳进而引起壳体振动,然后向外界辐射噪声[10]。

图1 电容器结构
1.2 电容器激励分析
对电容器内部芯子的受力分析如图2所示[11]。

图2 芯子元件受力分析
电容器加载基波电压和谐波电压激励时,处于其顶部和底部的极板均受到电场力作用,中间极板的电场力则保持相对平衡状态,并且芯子单元所产生的电场力有明显的指向性,方向分别指向电容器的顶部和底部,因此电力电容器外壳的底部和顶部振动最大。
为确定两极板电场力与主要电参数的关系,建立如图4所示的双极板电容器模型[12],进而得到两极板的电场力与激励电压之间的函数关系。
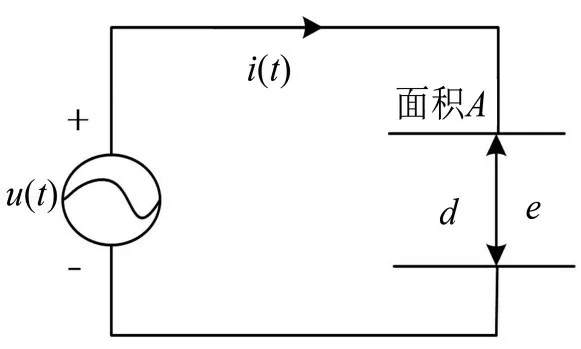
图3 双极板电容器模型
其中两极板之间电场力F(t)为

式中:F(t)为电场力,ε 为介电常数,A 为极板面积,d为电极间距,u(t)为电压。
电容器基波电压为

式中:U0为基波电压有效值,ω为角频率。
谐波电压为

式中:Un为谐波电压的有效值。
电容器中基波和多种谐波叠加的电压为

联立式(1)、式(2)、式(3)、式(4),则可得电场力为
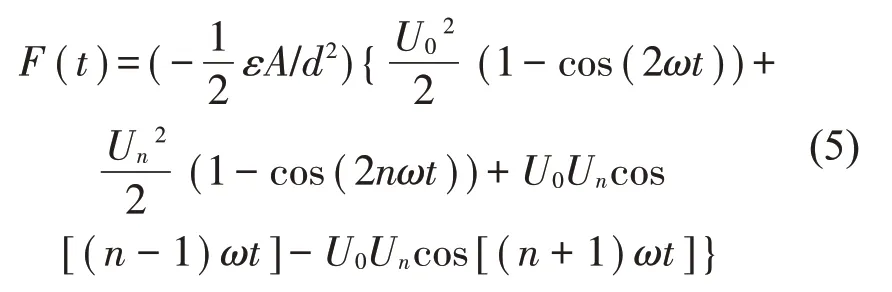
通过对电容器运行时所受电场力进行分析推导,可以看出,当电容器加载基波电压并叠加某n次谐波电压激励时,电容器元件除了受到谐波频率为2ω 的基波电场力外,还受到了谐波频率为2nω、(n-1)ω和(n+1)ω 3种不同谐波频率的电场力。
2 双底面隔声结构尺寸设计
2.1 双底面隔声结构隔声原理
双底面隔声结构是一种比较简单的轻质金属三明治板结构[13],其基本结构主要由两块矩形钢板和尺寸为l 的空气层组成,对此结构隔声原理进行分析。其声波的基本传递路径为“板-空气-板”,可以将此结构等效为弹簧阻尼减振系统,如图4所示。

图4 双底面结构等效模型
当电力电容器底面振动产生噪声后,声波从电容器底部传入,声压首先作用在双底面结构的上表面,其中有一部分声波被反射,另一部分通过金属板传播至空气层,中间空气层可以等效为弹性系数为k的弹簧,损耗一部分声波,剩余声波通过双底面结构的下表面传播至外界,进而辐射噪声,从而达到隔声的目的。
2.2 面向电容器噪声的双底面结构尺寸设计
本文仅对某出口电容器产品进行空腔结构空气层尺寸设计,首先通过试验的方法确定电力电容器辐射噪声的主要噪声频率,然后在LMS Virtual.lab中建立双底面结构的参数化模型,进而使用声振耦合的方法计算得到频率与隔声量的特性曲线。最后针对电力电容器特定噪声频率,以隔声量为优化目标优化出特定噪声频率下的最优空气层尺寸。
2.2.1 电容器底部噪声主要贡献频率的确定
单台电力电容器底部主要噪声频率主要通过振动噪声测试得到,也可以通过式(5)所示的电场力计算公式确定电场力的主要贡献频率,进而确定主要噪声频率。
图5 为电力电容器振动与噪声实验方案,所加电流激励为:50 Hz基频40 A电流同时叠加3次谐波6 A 电流、5 次谐波12 A 电流、7 次谐波5 A 电流、35次谐波9 A电流、37次谐波9 A电流、47次谐波18 A电流与49 次谐波12 A 电流。将上述激励参数代入式(5)可得电场力的主要谐频为1 700 Hz(35-1次谐频)、1 800 Hz(37-1 次谐频)、1 900 Hz(37+1 次谐频)、2 300 Hz(47-1 次谐频)、2 400 Hz(49-1 次谐频)、2 500 Hz(49+1次谐频)。

图5 电力电容器振动与噪声实验方案图
通过添加上述激励的50%电流和75%电流和全工况电流3 种不同工况的电流激励,得到表面振动响应和声学响应[14]。文中只列举全工况的测试结果,即电容器正常作业下实际工况的测试结果。电流装置系统主要施加基波电流激励和谐波电流激励,振动数据采集分析系统为PSV-400-3D激光测振仪,噪声采集分析系统为北京东方振动与噪声研究所研发的16通道噪声测试与分析系统,最高采样频率为51.2 kHz。将振动与噪声的测试结果在计算机上进行处理和分析,进而得到电力电容器底部测点的振动加速度响应和声学响应。
基于上述电力电容器振动与噪声测试系统,对电力电容器振动噪声进行测试,并对测试数据进行处理,得到如图6至图8所示的电力电容器底面振动加速度频谱图、底面振型和底面1/3 倍频程声压频谱图。

图6 电容器底面振动加速度频谱图
从图6 至图8 所示的测试结果可以看出所测试的电容器底面振动峰值主要集中在中高频,主要有1 700 Hz、1 800 Hz、1 900 Hz、2 300 Hz、2 400 Hz、2 500 Hz;电力电容器底面的辐射噪声的主要频率有:1 700 Hz、1 800 Hz、1 900 Hz、2 300 Hz、2 400 Hz、2 500 Hz,其中1 800 Hz 和2 500 Hz 频率下辐射噪声最大。其主要噪声贡献频率与式(5)计算得到电场力主要谐频一致,也验证了试验的准确性。测试结果显示主要噪声频率下的辐射噪声远大于其余噪声频率下的辐射噪声,因此有效解决主要噪声频率下的噪声对于电容器底面噪声问题的治理起着关键作用。

图7 电容器底面1阶振型

图8 电容器底面1/3倍频程声压频谱图
2.2.2 AML仿真技术方法
在声学试验中,通常利用混响室法对隔声产品进行隔声量测试,即在如图9 所示的声振测试环境中进行,左侧为混响室,右侧是消声室,基于此声振测试系统,测量出入射到混响室的声功率和辐射到消声室的声功率,从而准确测得隔声产品的隔声量,具体计算如式(6)所示。

式中:TL为隔声量,Wi为入射到混响室的声功率,Wo为辐射到消声室的声功率。

图9 声振测试系统简图
使用LMS Virtual.Lab 中Automatically Matched Layer (AML)技术方法模拟该过程[15]。在隔声结构两边添加AML网格层模拟混响室和消声室,左侧网格用来模拟混响室,右侧网格用来模拟消声室。在网格边界定义AML 属性,从而实现无反射边界的模拟。
2.2.3 双底面结构隔声量仿真计算
首先在LMS Virtual. Lab 仿真平台建立双底面结构的三维模型,双底面三维模型主要由6 块薄钢板和空气层组成,具体尺寸为:钢板长宽为383 mm×197 mm,钢板厚均为1.5 mm。本文将双底面结构的空气层尺寸参数化,为后续的尺寸优化提供优化变量,初始值设为25 mm。以图10 所示的AML 仿真方法添加混响室网格和消声室网格。消声室一侧距离双底面结构上表面5 mm,混响室一侧距离双底面结构下表面5 mm。

图10 声振测试系统模拟
将三维模型按照声学网格划分标准[15]进一步进行几何清理和网格划分。需要注意的是网格划分时把有限元模型的尺寸参数和空气层尺寸x 关联起来,为后续优化提供参数关联。划分好网格的双底面腔体结构有限元模型如图11所示,其中双底面结构腔体、消声室和混响室网格为声学体网格,赋予其空气的流体属性,双底层结构网格为结构面网格,赋予该1.5 mm 的2D 壳单元钢的材料属性,具体的材料属性见表1。

表1 电容器底部双底面结构材料属性

图11 附加消声室和混响室的空气层结构有限元模型
对于双底面结构隔声量求解,是采取直接声振耦合的计算方法求解其隔声量,具体包括AML属性的定义、耦合面的约束和声源的设定。计算得到如图12所示的的隔声量与频率之间的特性曲线。

图12 频率与隔声量特性曲线
2.2.4 双底面结构空气层的尺寸优化
利用LMS Virtual Lab 的Optimization 技术优化得到特定噪声频率下隔声量最大时的最优空气层尺寸,使用序列二次规划算法(SQP)进行优化。序列二次规划(SQP)算法[16]是一种基于梯度迭代的搜索算法,其优点在于初始点是可选的,计算量小,存储量小,并且在每次迭代中,目标函数的响应面被二次曲面局部逼近,使约束被线性化。从而使复杂优化问题简化,可以解析求解,导致在迭代的“线搜索”阶段可使用“最陡下降”的方向来改进目标函数,又能同时满足所有的约束条件。
LMS Virtual Lab 中序列二次规划算法(SQP)的计算流程为
(1)初始化,设置初始点。
(2)计算所有导数。
(3)求解二次规划子问题。
(4)计算拉格朗日乘子。
(5)使用外点罚函数进行搜索。
(6)检查收敛性。
针对双底面结构空气层尺寸优化问题建立如式(7)所示的单目标优化函数,采用SQP 算法进行优化。其中优化目标函数f(x)为特定频率下双底面结构的隔声量,x 为双底面腔体结构空气层尺寸,即优化变量,考虑到电容器产品尺寸问题,附加腔体尺寸不宜过大,所需优化计算的空气层尺寸变量取值范围为20 mm~50 mm。

根据电容器振动噪声试验可知,电力电容器主要噪声频率处于1 700 Hz~1 900 Hz、2 300 Hz~2 500 Hz 频带中,其中在噪声频率1 800 Hz 和2 500 Hz 处的辐射噪声最大。文中仅列举1 800 Hz 和2 500 Hz 两个主要频率处的优化结果。然后将LMS Virtual Lab 的Optimization 模块的优化数据结果导入MATLAB中处理,得到特定噪声频率下不同空气层尺寸的隔声量,如图13所示。

图13 特定噪声频率下不同空气层尺寸的隔声量
优化结果显示,对于电力电容器的特定噪声频率1 800 Hz,在44.7 mm 处的隔声效果最好,并且对于噪声频率2 500 Hz也取得不错的隔声效果。考虑到电容器的尺寸问题,将空气层的尺寸选为45 mm,用于电容器减振结构设计之中。
3 电力电容器振动噪声测试验证
振动噪声测试采用的测试系统和上节中确定主要噪声频率的测试系统一致。分别制作20 mm、25 mm、30 mm、35 mm、40 mm、45 mm 和50 mm7 种不同空气层尺寸的空腔结构,分别焊接到某型号电容器样品上。通过添加上节中所述的电流激励,进行振动噪声测试,并与上节中所示无腔体结构的电容器样品的测试结果进行对比。
图14为空气层尺寸为45 mm的电容器底面1阶振型,与图7所示的原电容器样品的底面1阶振型对比发现,底面振动得到了明显抑制,加速度幅值减小,这也验证了本文关于双底面结构的隔声原理分析的正确性。

图14 空气层尺寸为45 mm的电容器底面1阶振型
对采用PSV-400-3D 激光测振仪测试得到的电容器底面振动加速度数据进行统计,获得电容器底面振动加速度随空气层尺寸变化的特性曲线,如图15所示。观察变化趋势可知,总体来说随着空气层尺寸的变大,底面振动幅值呈现下降趋势,其中在空气层尺寸为45 mm 处表面振动加速度最小,减振效果最为明显,试验结果与LMS Virtual.Lab中的仿真结果在趋势上保持一致。

图15 空气层尺寸不同时的底面振动加速度
图16所示为用东方所噪声测试平台测试得到的附加45 mm 空气层的电力电容器底面的1/3 倍频程声压频谱图。

图16 空气层尺寸为45 mm时的底面1/3倍频程声压频谱图
观察声压频谱图可知,主要噪声频率集中在1 500 Hz~5 000 Hz,与未加腔体结构的电容器噪声频率一致。将用东方所噪声测试平台测试得到的空气层尺寸不同时的底面声压级进行统计,得到空气层尺寸不同时的电容器底面声压级,如图17所示。
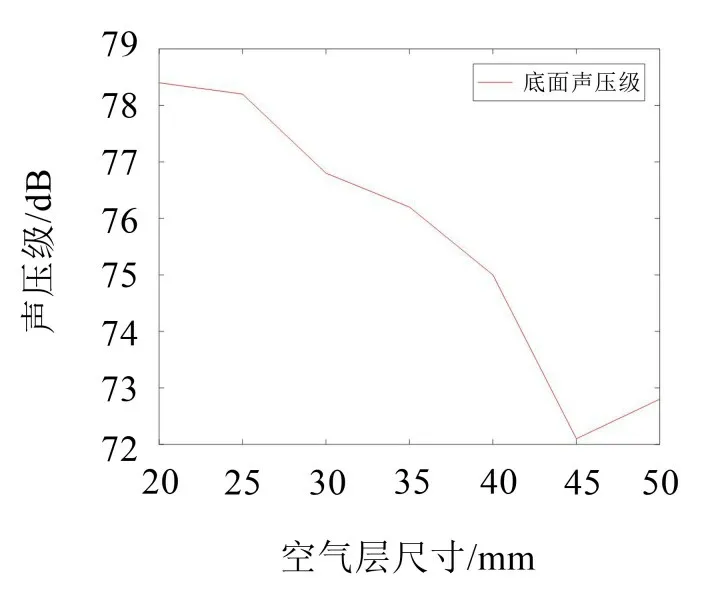
图17 空气层尺寸不同时的电容器底面声压级
通过观察可知,增加空气层结构后底部噪声得到明显抑制,将空气层尺寸为45 mm 与未加腔体结构的电容器底面声压级对比,发现底面降噪量达12.8 dB,并且在空气层尺寸为45 mm时辐射噪声声压值最小,在趋势上和仿真结果一致,验证了本文方法的可靠性。
4 结语
(1)分析电力电容器的振动噪声产生机理,并设计试验方案以确定电力电容器主要噪声频率。
(2) 分析双底面结构的隔声原理,并在LMS Virtual. Lab 中建立双底面结构的参数化有限元模型,计算得到空气层尺寸为25 mm 时的噪声频率和隔声量的特性曲线,并提出一种面向电容器特定噪声频率的双底面结构尺寸计算方法。
(3)设计了底部安装不同空腔尺寸的电力电容器样品,进行振动噪声对比测试,结果显示本文提出的双底面结构尺寸设计方法和实验数据在趋势上保持一致,验证了所提方法的准确性,该方法对于电力电容器底面降噪设计具有一定的工程意义。

